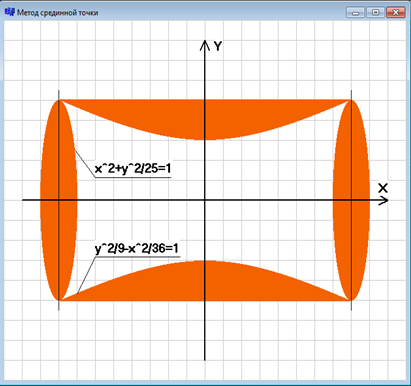
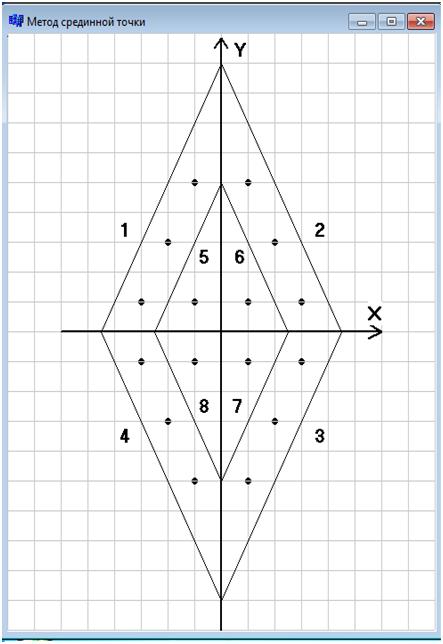
//программа написана на языке программирования C++Builder6
#include <vcl.h>
#pragma hdrstop
#include<math.h>
#define C_M Canvas->MoveTo
#define C_L Canvas->LineTo
#define C_P_C Canvas->Pen->Color
#define C_P_W Canvas->Pen->Width
#define C_T Canvas->TextOutA
#define C_P Canvas->Pixels
#define R_B RGB(200,200,200)
#define cW clWhite
#define cB clBlack
#define R_G clRed
#include «Article_9.h»
//———————————————————————————————
#pragma package(smart_init)
#pragma resource «*.dfm»
TForm1 *Form1;
int mx=30,my=30;
//———————————————————————————————-
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{ }
//———————————————————————————————-
void __fastcall TForm1::FormPaint(TObject *Sender)
{Color=(TColor)cW;
int xc=14*mx,yc=9.5*my,r=8.5*my,i;
int a=8*mx,b=2.5*my;
ShowGrid(xc);
//1
DrawCircle(xc,yc,r,true,cB);
DrawEll(xc,yc-2.5*my,a,b,true,cB);
//наклонные линии
//1
line(xc,yc-8.5*my,xc-5.25*mx,yc+6.6*my,R_G);
line(xc-1,yc-8.5*my+1,xc-5.25*mx-1,yc+6.6*my+1,R_G);
line(xc-1,yc-8.5*my+2,xc-5.25*mx-1,yc+6.6*my+2,R_G);
//2
line(xc,yc-8.5*my,xc+5.25*mx,yc+6.6*my,R_G);
line(xc-1,yc-8.5*my+1,xc+5.25*mx-1,yc+6.6*my+1,R_G);
line(xc-1,yc-8.5*my+2,xc+5.25*mx-1,yc+6.6*my+2,R_G);
//3
line(xc-8.1*mx,yc-2.5*my,xc,yc+6.6*my,R_G);
line(xc-8.1*mx-1,yc-2.5*my+1,xc-1,yc+6.6*my+1,R_G);
line(xc-8.1*mx-1,yc-2.5*my+2,xc-1,yc+6.6*my+2,R_G);
//4
line(xc+8.1*mx,yc-2.5*my,xc,yc+6.6*my,R_G);
line(xc+8.1*mx-1,yc-2.5*my+1,xc-1,yc+6.6*my+1,R_G);
line(xc+8.1*mx-1,yc-2.5*my+2,xc-1,yc+6.6*my+2,R_G);
//штриховка
//1
for(i=0;i<=20;i++)
line(xc-3*i,yc-8.5*my+9*i,xc+3*i,yc-8.5*my+9*i,R_G);
//2
for(i=0;i<=14;i++)
line(xc-7.9*i,yc+6.6*my-9*i,xc+7.9*i,yc+6.6*my-9*i,R_G);
//3
for(i=0;i<=14;i++)
line(xc-8.1*mx+9*i,yc-2.5*my,xc-8.1*mx+9*i,yc-2.5*my+10.3*i,R_G);
for(i=1;i<=5;i++)
line(xc-3.9*mx+9*i,yc-2.55*my,xc-3.9*mx+9*i,yc+2.55*my-27*i,R_G);
//4
for(i=0;i<=14;i++)
line(xc+8.1*mx-9*i,yc-2.5*my,xc+8.1*mx-9*i,yc-2.5*my+10.3*i,R_G);
for(i=1;i<=5;i++)
line(xc+2.1*mx+9*i,yc-2.55*my,xc+2.1*mx+9*i,yc-2.55*my+27*i,R_G);
//горизонтальные линии
//1
line(xc-8.1*mx,yc-2.5*my,xc+8.1*mx,yc-2.5*my,R_G);
line(xc-8.1*mx-1,yc-2.5*my-1,xc+8.1*mx-1,yc-2.5*my-1,R_G);
line(xc-8.1*mx-1,yc-2.5*my+1,xc+8.1*mx-1,yc-2.5*my+1,R_G);
//2
line(xc-5.25*mx,yc+6.65*my,xc+5.25*mx,yc+6.65*my,R_G);
line(xc-5.25*mx-1,yc+6.65*my-1,xc+5.25*mx-1,yc+6.65*my-1,R_G);
line(xc-5.25*mx-1,yc+6.65*my+1,xc+5.25*mx-1,yc+6.65*my+1,R_G);
//3
line(xc-3.8*mx,yc+2.4*my,xc+3.8*mx,yc+2.4*my,R_G);
line(xc-3.8*mx-1,yc+2.4*my-1,xc+3.8*mx-1,yc+2.4*my-1,R_G);
line(xc-3.8*mx-1,yc+2.4*my+1,xc+3.8*mx-1,yc+2.4*my+1,R_G);
C_P_C=(TColor)cB;
XoY(xc,yc);}
//——————————————————————————————
void __fastcall TForm1::ShowGrid(int cenx)
{int x,y;
C_P_C=(TColor)R_B;
//горизонтальные линии сетки
for(y=0;y<=19*my;y+=my)
{C_M(0,y);
C_L(28*mx,y);}
//вертикальные линии сетки
for(x=0;x<=28*mx;x+=mx)
{C_M(x,0);
C_L(x,19*my);}}
//———————————————————————————————-
void __fastcall TForm1::XoY(int cenx, int ceny)
{//оси
//ось X
C_P_W=2;
C_M(cenx-10*mx,ceny);
C_L(cenx+10*mx,ceny);
//стрелка
C_M(cenx+9.5*mx,ceny-0.25*my);
C_L(cenx+10*mx,ceny);
C_L(cenx+9.5*mx,ceny+0.25*my);
C_T(cenx+9.5*mx,ceny-1*my,»X»);
//ось Y
C_M(cenx,ceny-9.4*my);
C_L(cenx,ceny+9.4*my);
//стрелка
C_M(cenx-0.25*mx,ceny-9*my);
C_L(cenx,ceny-9.4*my);
C_L(cenx+0.25*mx,ceny-9*my);
C_T(cenx+0.5*mx,ceny-9.6*my,»Y»);
C_P_W=1;}
//———————————————————————————————
void __fastcall TForm1::line(int x1, int y1, int x2, int y2, int color)
{float k,x,y,c=0;
if (x1==x2) k=y2;
else k=(float)(y2-y1)/(x2-x1);
C_P[x1][y1]=(TColor)color;
if (fabs(x2-x1)>fabs(y2-y1))
{ y=y1;
if (k>=0)
{ for(int x=x1+1;x<=x2;x++)
{ if ((c+=k)>0.5)
{ c-=1;
y++;}
C_P[x][(int)y]=(TColor)color;
}
}
else
{ y=y1;
for(int x=x1-1;x>=x2;x—)
{ if ((c-=k)>0.5)
{ c-=1;
y++; }
C_P[x][(int)y]=(TColor)color;
}
}
}
else
{ x=x1;
if ((1./k)>=0)
{ for(int y=y1+1;y<=y2;y++)
{ if ((c+=1./k)>0.5)
{ c-=1;
x++; }
C_P[(int)x][y]=(TColor)color;
}
}
else
{ x=x1;
for(int y=y1+1;y<=y2;y++)
{ if ((c-=1./k)>0.5)
{ c-=1;
x—; }
C_P[(int)x][y]=(TColor)color;
}
}
}
}
//——————————————————————————————
void __fastcall TForm1::DrawCircle(int cenx, int ceny, int r, bool dotted,
int color)
{int x,y,d;
x=0;y=r;d=1.25-r;
C_P[x][y]=(TColor)color;
int counter=0;
while (y>x)
{ if (d<0)
{ d+=2*x+3;
x++; }
else
{ d+=2*(x-y)+5;
x++;
y—;}
if (dotted && ((counter %20) !=9) && ((counter %20) !=10)&&
((counter %20!=11))) DrawPoints(cenx,ceny,x,y,color);
if (!dotted) DrawDot(cenx,ceny,x,y,color);
++counter; }}
//————————————————————————————————
void __fastcall TForm1::DrawPoints(int cenx, int ceny, int x, int y, int color)
{C_P[cenx+x][ceny-y]=(TColor)color;
C_P[cenx+y][ceny+x]=(TColor)color;
C_P[cenx-x][ceny+y]=(TColor)color;
C_P[cenx-y][ceny-x]=(TColor)color;
C_P[cenx-y][ceny+x]=(TColor)color;
C_P[cenx-x][ceny-y]=(TColor)color;
C_P[cenx+y][ceny-x]=(TColor)color;
C_P[cenx+x][ceny+y]=(TColor)color;}
//——————————————————————————————-
void __fastcall TForm1::DrawEll(int cenx, int ceny, int a, int b,
bool dotted, int color)
{int x,y,a2,b2,a2a,b2b,k, counter=0;
float d,st;
a2=a*a;b2=b*b;
a2a=2*a2;b2b=2*b2;
//часть 7
d=b2+a2*(-b+0.25);
x=0;y=b;k=0;
while(a2*(y-0.5)>b2*x)
{if (d<0)
{d+=b2*(2*x+3);x++;}
else
{d+=b2*(2*x+3)+a2a*(1-y);x++;y—;}
if (dotted && ((counter %20) !=9) && ((counter %20) !=10) &&
((counter %20) !=11)) DrawDot(cenx,ceny,x,y,color);
if (!dotted) DrawDot(cenx,ceny,x,y,color);
++counter;}
//часть 8
d=-a2+b2*(-a+0.25);
x=a;y=0;st=sqrt(a2+b2);
while((a2*y<=b2*(x-0.5)) && (x>=a2/st) && (y<=b2/st))
{if (d<0)
{d+=a2*(2*y+3);y++;}
else
{d+=b2b*(1-x)+a2*(3+2*y);y++;x—;};
if (dotted && ((counter %20) !=9) && ((counter %20) !=10) &&
((counter %20) !=11)) DrawDot(cenx,ceny,x,y,color);
if (!dotted) DrawDot(cenx,ceny,x,y,color);
++counter;
C_P_C=(TColor)color;}}
//————————————————————————————————
void __fastcall TForm1::DrawDot(int cenx, int ceny, int x, int y, int color)
{C_P[cenx+x][ceny+y]=(TColor)color;
C_P[cenx+x][ceny-y]=(TColor)color;
C_P[cenx-x][ceny+y]=(TColor)color;
C_P[cenx-x][ceny-y]=(TColor)color;}
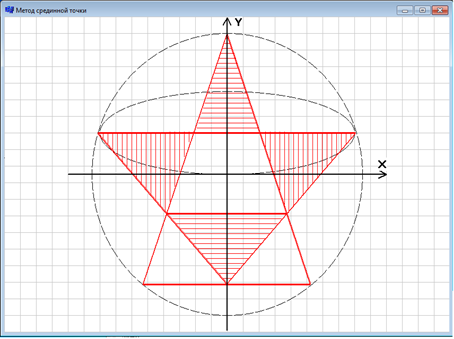
Рисунок 1. Построение заданной фигуры
Список литературы:
- Шикин Е.В., Боресков А.В. Компьютерная графика. Полигональные модели. — М.: ДИАЛОГ-МИФИ, 2005.-464с.: ил.[schema type=»book» name=»ИСПОЛЬЗОВАНИЕ МЕТОДА СРЕДИННОЙ ТОЧКИ ДЛЯ ПОСТРОЕНИЯ ЗАДАННОЙ ФИГУРЫ» description=»В компьютерной графике рассматриваются растровые алгоритмы. Приводится программа построения заданной фигуры по методу срединной точки. Алгоритмы растровой развёртки отрезка линии, окружности и эллипса описывается в [1]. Для устранения ступенчатости при построении линейных функций (линий), а также конических сечений (окружностей, эллипсов, парабол, гипербол) помимо алгоритма Брезенхема можно воспользоваться методом срединной точки.» author=»Ананьева Марина Алексеевна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2016-12-27″ edition=»euroasia-science.ru_26-27.02.2016_2(23)» ebook=»yes» ]