В работах [1-7] для уменьшения уровня рассеянного поля радиолокационных объектов предлагается использовать различные конструкции одиночных щелевых импедансных нагрузок, построенных на базе единой математической модели, представленной в виде двух областей, связанных между собой через отверстие в бесконечном идеально проводящем экране.
На основе этой же математической модели в работе [8] исследованы характеристики одиночной щелевой импедансной нагрузки на основе отверстия в бесконечном идеально проводящем экране.
В данной работе исследована эта же конструкция щелевой импедансной нагрузки, но в составе бесконечной решетки, с целью определения возможности регулировки эквивалентного поверхностного импеданса путем изменения ширины полоскового проводника, размещенного в раскрыве отверстия.
Постановка задачи. Имеется бесконечная решетка щелевых импедансных нагрузок (рис.1), размещенных с периодом T. Каждый элемент решетки представляет собой щель в плоском идеально проводящем экране, расположенном в плоскости x0z.
Область V1 с параметрами 
занимает все полупространство над идеально проводящим экраном. Первичное поле возбуждается в области V1 плоской волной, падающей под углом Θ, отсчитываемым от нормали к поверхности экрана. Область V2 с параметрами 
не содержит
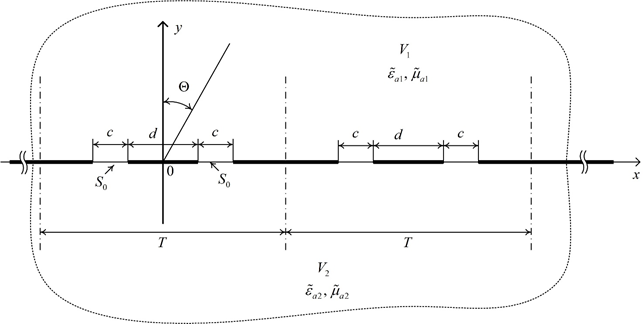
Рисунок 1. Постановка задачи
возбуждающих источников и ее геометрия не отличается от геометрии области V1 ( 
— абсолютные комплексные диэлектрическая и магнитная проницаемости сред соответствующих областей). Область V2 связана с областью V1 через одно или нескольких отверстий S0 (щель шириной c, в раскрыве которой расположен полосковый проводник шириной d).
Характеристики возбуждающих источников и параметры конструкции будем считать независимыми от координаты z (двумерная задача), имеются составляющие полей 
, (H — поляризация). Требуется найти усредненный по периоду решетки T эквивалентный поверхностный импеданс.
Поля в области V1. В силу периодичности структуры рассеянное поле в области V1 можно представить в виде разложения по пространственным гармоникам Флоке
Используя ортогональность гармоник Флоке, из (2) найдем коэффициенты разложения тока Im и, подставляя их в (1), окончательно получим выражение для магнитного поля в области V1 в раскрыве отверстия (y=0)
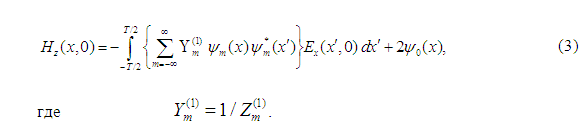
Поля в области V2. Запишем выражения для поля в области V2 также в виде разложения по гармоникам Флоке. Используя граничное условие для электрического поля в плоскости y — 0 и условие ортогональности гармоник Флоке, окончательно получим выражение для поля в области V2 при
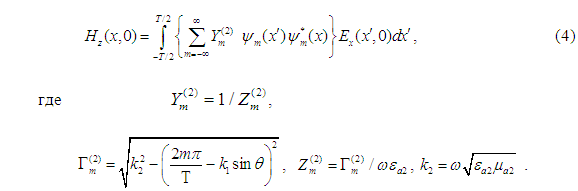
Интегральное уравнение. Удовлетворяя условию непрерывности касательных составляющих полей в раскрыве отверстия, из (3) и (4) получим интегральное уравнение относительно неизвестной касательной составляющей электрического поля 
в раскрыве отверстия
Численная реализация решения. Для численной реализации полученного интегрального уравнения (5) использовался метод Крылова- Боголюбова, в результате чего указанное интегральное уравнение сводилось к системе линейных алгебраических уравнений следующего вида
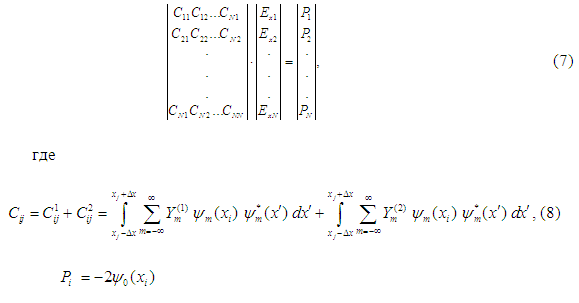
При вычислении элементов 
возникают определенные математические трудности, связанные с наличием логарифмической особенности. Поэтому для выделения этой особенности в явном виде, а также для сокращения времени машинных расчетов была улучшена сходимость ряда в (8), для чего было применено преобразование Куммера, после чего элементы принимают окончательный вид:
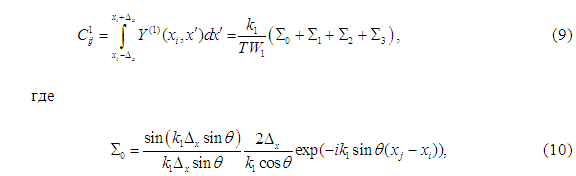
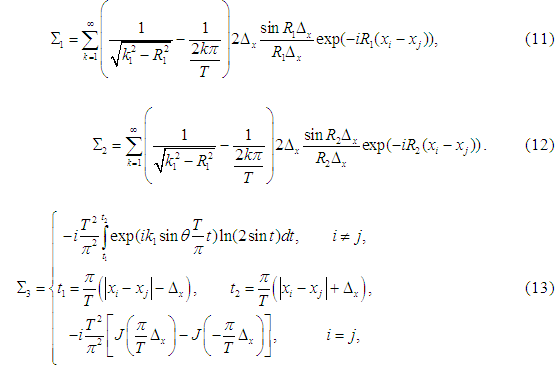
Численные результаты. В результате решения задачи были рассчитаны зависимости комплексного эквивалентного поверхностного импеданса 
от размера отверстия c, от ширины полоскового проводника d и от угла падения ЭМВ Θ.
Все виды зависимостей приведены для активной и реактивной составляющих ЭПИ, нормированных на сопротивление свободного пространства W0=120p Ом. Все расчеты выполнялись для параметров сред 
, 
.
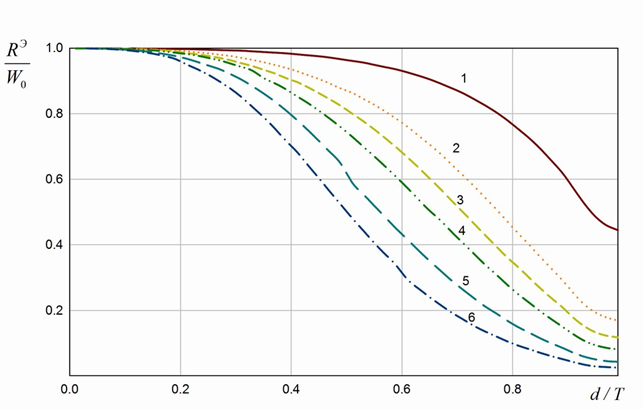
На рис. 2а, 2б представлены зависимости активной и реактивной составляющих ЭПИ от ширины проводника , нормированной на величину интервала усреднения импеданса , для случая при разных
а)
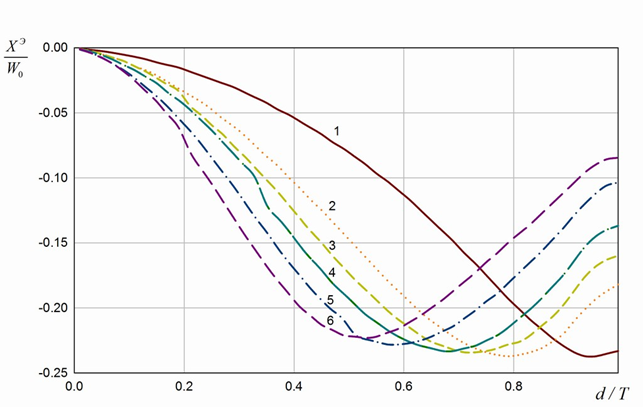
б)
Рисунок 2. Зависимость ЭПИ от ширины полоскового проводника d
при фиксированных значениях интервалах усреднения импеданса T.
(1 – Т=0.1λ, 2 — Т =0.2 λ, 3 — Т =0.249λ , 4 — Т =0.3λ , 5 — Т =0.4λ,
6 — Т =0.499λ) а) действительная часть, б) мнимая часть.
величинах интервала усреднения импеданса T. Из графиков видно, что при малых значениях ширины полоскового проводника 
активная часть ЭПИ практически равна волновому сопротивлению свободного пространства W0, т.е. полосковый проводник из-за своей малой ширины фактически не оказывает никакого влияния на значение ЭПИ. При дальнейшем увеличении ширины d до значений, близких к интервалу усреднения импеданса Т, значения как активной, так и реактивной составляющей импеданса начинают стремиться к нулю.
Таким образом, полученные результаты численного исследования бесконечной решетки щелевых импедансных нагрузок, выполненных на основе щели в экране, показали, что
- с помощью данной конструкции можно реализовать комплексные значения ЭПИ, причем в рассматриваемом случае Н-поляризации значения ЭПИ для данной конструкции носят резистивно-емкостной характер;
- величину ЭПИ можно регулировать путем изменения ширины полоскового проводника в раскрыве щели.
Список литературы:
- Кошкидько В.Г., Петров Б.М., Юханов Ю.В. Эквивалентный поверхностный импеданс пассивных импедансных нагрузок, выполненных на основе отверстия в экране, нагруженного двумерной полостью // Радиотехника и электроника, 1997, т.42, № 6, c. 652-661.
- Кошкидько В.Г., Ганжела Н.В. Эквивалентный поверхностный импеданс щелевых импедансных нагрузок, выполненных на основе связанных прямоугольных областей // Радиотехника и электроника, 1999, Т 44. № 8. С.947-954.
- Кошкидько В.Г., Алпатова О.В. Эквивалентный поверхностный импеданс щелевой импедансной нагрузки на основе полуцилиндрической полости // Радиотехника и электроника. 1999. Т.44. № 1. С.25-28.
- Кошкидько В.Г., Алпатова О.В. Эквивалентный поверхностный импеданс щелевой импедансной нагрузки, выполненной на основе отверстия в экране. Случай Е-поляризации // Радиотехника и электроника. 2003. Т.48. №1. С.57-63.
- Петров Б.М., Кошкидько В.Г. Метод анализа электромагнитных полей, рассеянных щелью в цилиндрическом резонаторе с фланцем // Радиотехника и электроника. 1988, т.33, № 10, с.2060-2064.
- Short J.R., Chen K.M. Backscattering from an Impedance loaded slotted cylinder// IEEE Trans., 1969, vol.AP-17, №3.
- Петров Б.М., Шарварко В.Г. Синтез поверхностного импеданса кругового цилиндра по заданной диаграмме рассеяния// Cб. науч. метод. статей по прикладной электродинамике. М.,1979. Вып. 3. С.62-78.
- Кошкидько В.Г., Алпатова О.В., Сердюк Э.С. Численное исследование характеристик щелевой импедансной нагрузки на основе отверстия в бесконечном идеально проводящем экране // Известия ЮФУ. Технические науки. 2014. № 11, с. 58-67.
- Цалиев Т.А., Черенков В.С. Возбуждение одиночной канавки и эквивалентный поверхностный импеданс ребристых структур // Радиотехника и электроника. 1985. т. 30. №9. с. 1689.[schema type=»book» name=»ЭЛЕКТРОДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ БЕСКОНЕЧНОЙ РЕШЕТКИ ЩЕЛЕВЫХ ИМПЕДАНСНЫХ НАГРУЗОК, ВЫПОЛНЕННЫХ НА ОСНОВЕ ЩЕЛИ В БЕСКОНЕЧНОМ ИДЕАЛЬНО ПРОВОДЯЩЕМ ЭКРАНЕ » description=»Решена задача о возбуждении плоской волной бесконечной решетки щелевых импедансных нагрузок, выполненных на основе щели в бесконечном идеально проводящем экране, с целью определения эквивалентного поверхностного импеданса. Задача решена методом интегральных уравнений, для численной реализации которого использован метод Крылова-Боголюбова. Представлены результаты численного эксперимента в виде зависимостей эквивалентного поверхностного импеданса от размеров полоскового проводника в раскрыве щели при фиксированных значениях интервала усреднения.» author=»Кошкидько Владимир Георгиевич, Алпатова Ольга Витальевна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-18″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_28.11.15_11(20)» ebook=»yes» ]