Пусть требуется минимизация функционала
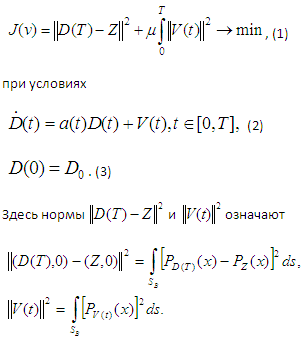
Класс управлений является область-функция 
, в которой 
, здесь M совокупность выпуклых замкнутых ограниченных множеств в Rn. Другими словами, на класс управлений не налагаются никакие ограничения и предполагаем, что решение рассматриваемой задачи, в указанном классе, существует. В этом случае из условия оптимальности
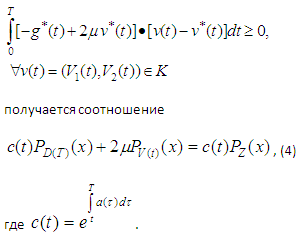
Таким образом, оптимальная пара определяется соотношением (1)-(4). Как видно, все эти соотношения задаются равенствами. Значит, мы можем предполагать, что при естественных условиях, решение задачи (1)-(3) непрерывно зависит от исходных данных. Также известно, что можно построить нейронную сеть, которая аппроксимирует непрерывное отображение с любой точностью. Используя это, решаем задачи (1)-(4) с помощью нейронных сетей.
Для этого сначала выбираем многослойную нейронную сеть и определяем ее весовые коэффициенты. Для этого используется в основном два подхода. Первый- аналитический, в котором весовые коэффициенты задаются по каким то формулам и другой, в котором весовые коэффициенты восстанавливаются в процессе обучения. Здесь мы будем использовать второй подход. В этом подходе точность решения зависит от количества входных и выходных данных и способа обучения нейронных сетей. Выбор входных и выходных данных является самым трудным и актуальным этапом при применении нейронных сетей.
Для применения нейронных сетей к решению задачи оптимального управления (1)-(3), нам нужны в достаточном количестве входные и выходные данные для процесса обучения. Как находим эти данные?
Здесь мы будем предлагать схему, для определения в достаточном количестве входные и выходные данные.
Исходные данные для задачи (1)-(3) являются 
. Задавая эти данные, определяется решение V(t). Для различных исходных данных решать задачи (1)-(3) является проблематично, так как, нашей целью является найти решение этой задачи именно для конкретно заданного 
. Для определения входных и выходных данных применяем «обратный» подход. Константа не варьируем, т.е. фиксируем. Возьмем область-функцию и непрерывную функцию 
Подставляя эти данные в уравнение (1) и начальное условие (2), находим V1(t) и
Значит, мы нашли входные данные , в которых решением задачи (1)-(3) является управление V1(t). Это есть соответствующий выходной данный. Однако, в этом процессе есть две проблемы. Первая, выбранные область функция и непрерывная функция должны быть такими, чтобы найденная по формулам (6) область функция, для любого t ∈ [0, T] была выпуклой. Второе, определяемое по формулам (6) множество не должно зависеть от t. Остается обеспечивать эти условия.
Для этого, например, можно взять в виде
.
Здесь Ai некоторые выпуклые множества βi(t) и 
, положительные , непрерывно-дифференцируемые функции. Из условий (5), (7), получим
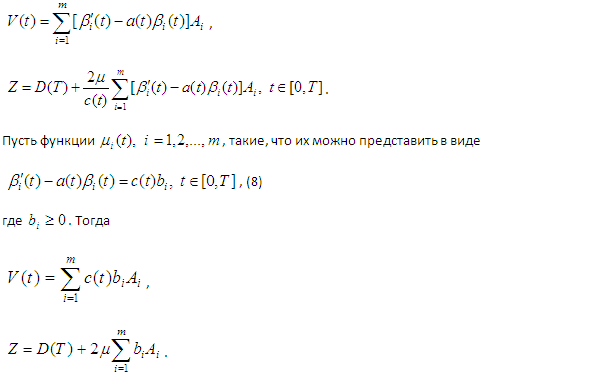
Так как, 
, вышеотмеченные два условия обеспечены.
Покажем, что существуют функции βi(t), которые удовлетворяют указанным условиям. Из уравнения (8) находим
Таким образом, взяв входные данные 
, мы получили выходной данный V1(t). Взяв аналогично, сколь угодно входные
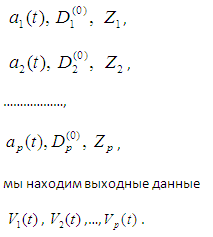
Используя эти данные можно проводить процесс обучения нейронной сети и найти весовые коэффициенты. После построения сети можно решать задачи (1)- (3) с любыми конкретными данными. Качество решений и надежность нейронной сети зависит от качества выбора и количества исходных данных. При увеличении погрешность приближенного решения уменьшается.
Список литературы:
- Aliev F.A., Niftiyev A.A., Zeynalov C.I. Optimal synthesis problem for the fuzzy systems. Optimal control, applications and methods. Published online in Wiley Online Library (wileyonlinelibrary.com). DOI: 10.1002/oca.964.
- Aliev F.A., Niftiyev A.A., Zeynalov C.I. Optimal synthesis problem for the fuzzy systems in semi-infinite interval. Appl. Comput. Math., 10(1), Special Issue, 2011, pp.97-105.
- Levin A. U., Narendra K.S.: Control of Nonlinear Dynamical Systems Using Neural Networks: Controllability and Stabilization. IEEE Transactions on Neural Networks, 1993, Vol. 4, pp.192-206
- Нейрокомпьютеры и их применение: Книга 6 – «Нейроматематика» (под редакцией А.И.Галушкина), Москва, ИПРЖР, 2002, 448с.
- Нифтиев A.A., Ахмедов Э.Р. Алгоритм для численного решения задачи вариационного исчисления с неизвестными границами. Вестник БГУ, 2005, № 1, стр. 25-30.
- Niftiyev A.A., Zeynalov C.I., Efendiyeva H.C. Mathematical modeling for the optimal use of a bounded area.Actual problems of economics. 2011, №2(116), pp.261-270.
- Niftiyev A.A., Maryam Pur, Zeynalov C.I. Fuzzy optimal control problem with non-linear functional. News Baku State University, 2010, №3.
- Niftiyev A.A., Zeynalov C.I., Majidzadeh K. Optimal using of a bounded area problem and its investigation by neural networks. Известия НАН Азерб. 2010, № 6, p. 75-82.[schema type=»book» name=»ПРИМЕНЕНИЕ НЕЙРОННЫХ СЕТЕЙ К РЕШЕНИЮ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ОТНОСИТЕЛЬНО МНОЖЕСТВА» description=»Пpeдложeньı мeтодьı peщeния задач оптимизации с помощью нeйронньıх сeтeй,в частности к peщeнию задач нечесткого линейного программирования. Для этого выбрана многослойная нейронная сет. Известно, что для выбора структуры нeйронньıх сетей не сушествует конкретного подхода. Этот выбор в основном зависит от количества входных и выходных данных и способа обучения нейронных сетей. Выбор входных и выходных данных является самым трудным и актуалным этапом при применении нeйронньıх сетей.» author=»Зейналов Джаваншир Ибрагим оглу, Алийев Мафтун Эйнулла оглу, Алийев Мафтун Эйнулла оглу,» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-05″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.11.16_31″ ebook=»yes» ]