Прогресс в различных отраслях техники во многом связан с возможностью применения новых композиционных материалов с регулируемыми прочностными характеристиками. Важное место среди них занимают многокомпонентные материалы, представляющие композиции сверхпрочных армирующих элементов (различных волокон, чешуек, частиц, «усов», стеклянных микросфер и т.д.) и связующего, механические свойства которых имеют значительный разброс. Поэтому исследование влияния статистического разброса упругих и прочностных свойств субструктурных элементов является актуальной задачей, решение которой позволит наиболее достоверно прогнозировать предельное состояние композита.
Структурный подход для исследования начального разрушения многофазных сред в случае детерминированных параметров предложен в [1, 2]. В целях конкретизации, как и в [1, 2], будем рассматривать плоское напряженное состояние в случае продольного или поперечного расположения фаз. Тогда согласно [1, 2] нагрузка начального разрушения в пространстве параметров внешнего воздействия 
определяется численно при решении задачи минимизации:
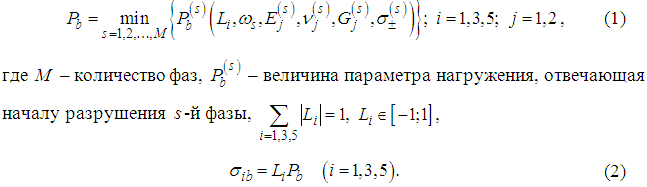
Здесь и в дальнейшем, если специально не оговорено, будем использовать обозначения и необходимые соотношения из [1, 2].
Для оценки влияния отклонений механических характеристик субструктурных элементов из (1) от номинальных значений на величину , тем самым, и на условие прочности композитного материала в пространстве , будем использовать метод статистических испытаний [3-5][3, 4, 5].
Для учета стохастической природы композита будем считать, что параметры
Таблица 1.
Параметры фаз микронеоднородного материала
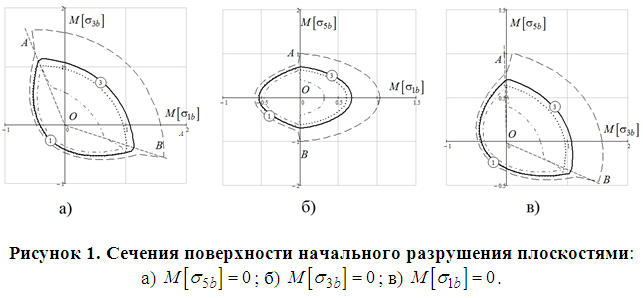
На рисунке 1 приведены различные сечения поверхности начального разрушения трехфазного композита при продольном расположении фаз для числа статистических испытаний K — 5, доверительной вероятности 
, статистики Стьюдента 
. Сплошные линии соответствуют математическому ожиданию разрушающей нагрузки; кривые, отмеченные точками, найдены при детерминированных параметрах, которые равны математическим ожиданиям всех величин из таблицы 1; штриховые и штрихпунктирные линии указывают доверительные интервалы из (8); участки кривых, отмеченные цифрами 1, 2 и 3 соответствуют разрушению 1-й, 2-й или 3-й фаз. В угловых точках и имеем одновременное разрушение двух фаз, поэтому при нагружении по лучам и имеем разрывы для линий, характеризующих доверительные интервалы.
На рисунке 2 представлены результаты для двадцати статистических испытаний при тех же значениях параметров.
Таким образом, предложенный подход для расчета предельного состояния микронеоднородных материалов позволяет учитывать стохастическую природу механических характеристик субструктурных элементов и определять область значений внешней нагрузки, в которой разрушение композита будет происходить с заданной вероятностью в зависимости от количества статистических испытаний и величины доверительной вероятности.
Список литературы
| 1. | Резников Б.С., Шеремет О.В. Анализ влияния различных критериев прочности элементов композиции на начальное разрушение макронеоднородных сред // Сборник научных трудов SWorld по материалам международной научно-практической конференции «Современные проблемы и пути их решения в науке, транспорте, производстве и образовании 2011», Том 11. Физика и математика. — Одесса, 2011. — С. 85-92. |
| 2. | Максименко В.Н., Резников Б.С., Шеремет О.В. Структурный анализ прочности макронеоднородных сред при плоском напряженном состоянии// Вестник Сибирского государственного университета им. ак. М.Ф. Решетнева, Красноярск, 2012. Вып. 1(41). — С. 31-34. |
| 3. | Метод статистических испытаний (метод Монте -Карло) / Н.П. Бусленко, Д.И. Голенко, И.М. Соболь, В.Г. Срагович, Ю.А. Шрейдер. — М.:Физматгиз, 1962. — 332 с. |
| 4. | Резников Б.С. Расчет на прочность конструкций из армированных материалов методом Монте-Карло// Механика композитных материалов, 1986. — №6. — С. 1059-1063. |
| 5. | Резников Б.С. Прогнозирование разрушения кольцевых пластин с учетом реальной структуры и стохастической природы армированного материала // Краевые задачи и их приложения: межвузовский сборник научных трудов. — Чебоксары: Изд-во Чуваш. ун-та, 1989. — С. 89-99. |
| 6. | Вентцель Е.С. Теория вероятностей. — М.: Наука, 1964. — 576 с. |
| 7. | Математическая статистика: учебник / В.М. Иванова, В.Н. Калинина, Л.А. Нешумова, И.О. Решетникова. — 2-е изд. перераб. и доп. — М.: Высшая школа, 1981. — 371 с. |
| 8. | Скудра А.М., Булавс Ф.Я., Роценс Н.А. Ползучесть и статическая усталость армированных пластиков. — Рига: Зинатне, 1971. — 238 с. |
| 9. | Игнатов И.В., Стрельченко И.Г., Юрьев С.В. Статистические характеристики механических констант стеклопластиков// Механика полимеров, 1972. — №6 — С. 1025-1028. |
| 10. | Тарнопольский Ю.М., Скудра А.Н. Конструкционая прочность и деформативность стеклопластиков — Рига: Зинатне, 1966. — 260 с. |
| 11. | Тарнопольский Ю.М., Розе А.В. Особенности расчета деталей из армированных пластиков. — Рига: Зинатне, 1969. — 274 с. |
| 12. | Дубровский И.М., Егоров Б.В., Рябошапка К.П. Справочник по физике. — Киев: Наукова думка, 1986. — 558 с. |
[schema type=»book» name=»ВЛИЯНИЕ СТОХАСТИЧЕСКОЙ ПРИРОДЫ МЕХАНИЧЕСКИХ СВОЙСТВ ЭЛЕМЕНТОВ СУБСТРУКТУРЫ НА ПРЕДЕЛЬНОЕ СОСТОЯНИЕ МИКРОНЕОДНОРОДНЫХ СРЕД» description=»На основе математической модели для микронеоднородных сред предложен метод и разработан программный комплекс для исследования начального разрушения материалов с внутренней структурой, учитывающий стохастическую природу механических свойств элементов композиции. В случае плоского напряженного состояния для трехфазных композитов проведено исследование влияния количества статистических испытаний, величины доверительной вероятности, объемного содержания фаз и их механических характеристик на предельное состояние композита и соответствующий доверительный интервал для разрушающих нагрузок. Предложенный подход дает возможность прогнозировать более эффективные конструкционные композиты с требуемыми по условиям эксплуатации прочностными характеристиками.» author=»Резников Борис Самуилович, Шеремет Оксана Владиславовна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-26″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_31.10.15_10(19)» ebook=»yes» ]