Введение
При оценке качества изображения известного объекта используются традиционные скалярные показатели качества [1,2]. Исторически сложилось, что качество исходного малоконтрастного изображения неизвестного объекта, формируемого в результате его обработки фильтрами различной структуры, оценивается при зрительном восприятии. В этой ситуации исходное изображение получено при наличии фонового излучения, статистические характеристики которого неизвестны. Поэтому его фильтрацию проводят с использованием фильтров различной структуры (оптимальными при выбранной модели формирования изображения, нелинейными, эвристическими [1÷6]). В силу индивидуальных особенностей зрительского восприятия часто возникают дискуссии, какой алгоритм из числа используемых приводит к лучшим результатам.
Как следствие, возникает необходимость выбора количественных характеристик, использование которых позволяло бы оценивать качество и сложность анализируемого изображения.
Обоснование ввода интегральных показателей качества и характеристик их поведения
Известно, что для сигналов (одномерных функций) в качестве достаточной количественной характеристики можно использовать значение информации по Шеннону [7], вычисляемое с помощью следующего выражения:
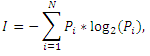
где Pi – вероятность появления i-значения наблюдаемого параметра из числа N возможных значений.
Использования информации при анализе свойств изображения недостаточно, поскольку при ее вычислении не учитывается пространственная структура двухмерного изображения на плоскости. В работе [8] для оценки свойств изображения было предложено использовать двумерные вариации Кронрода. А.С. Кронродом было показано [9], что функция двух переменных характеризуется не одним, а двумя функционалами (вариациями), которые в некотором смысле независимы. Эти функционалы были определены следующим образом:

Выбор анализируемых показателей качества и характеристик их поведения при анализе цифровых малоконтрастных изображений
Для детального описания содержащейся в цифровом изображении информации введём вектор P= P(G), компоненты которого – это значения нормированной гистограммы интенсивности, т. е. гистограммная оценка плотности вероятности распределения интенсивности изображения.
Для полного анализа поведения пространственной структуры цифрового изображения введём вектора V0 и V1, которые являются дискретными аналогами ранее введенных непрерывных функций v0 (et) и v1(et). Их поведение позволяет оценить гладкость, изменчивость и сложность изображения как функций уровней интенсивности. Отметим, что вектор нулевой вариации V0 является в определенном смысле топологической характеристикой изображения, основанной на понятии связности и не изменяющейся при гомеоморфизме, в частности, в группе аффинных преобразований. Значения его элементов при выбранном уровне интенсивности совпадают с числом локальных связных областей. В качестве метрической характеристики выступает вектор V1. Соответствующие значения его элементов – периметры выделенных связных областей.
Введём следующие интегральные показатели качества цифрового малоконтрастного изображения:
- показатель информации, который является значением информации по Шеннону,
- показатель топологии w0, вычисляемый по формуле w0(G) = 〈1|V0〉/N
- показатель метрики w1, вычисляемый по формуле w1(G) = 〈1|⌈V1〉/N
Здесь N — общее число возможных градаций интенсивности в изображении, <1| – вектор-строка, все компоненты которого равны единице, 〈1|V0〉 — операция скалярного произведения, G — анализируемое цифровое изображение, заданное в виде прямоугольной матрицы.
Введем дополнительный показатель качества – показатель компактности µ, значение которого при выбранном пороговом уровне интенсивности l для формирования битового изображения вычисляется по формуле
![]()
где: С=4 – нормировочный коэффициент, P (l) – периметр контура выделенного битового изображения; S (L) – его площадь.
Данный показатель является избыточным, однако его использование достаточно при решении задачи выделения области локализации изображения неизвестного объекта на исходном снимке [6].
Пример анализа медианной фильтрации изображения, полученного на фоне помех.
В качестве примера использования предложенных показателей качества на следующем рисунке слева направо приведены изображения круга, полученного при наличии сложного фонового излучения, а также изображений на выходе медианных фильтров 3-о, 5-о, 7-о порядков, под которыми принято понимать размер квадратного ядра фильтрации цифрового изображения. Медианный фильтр решает задачу фильтрации фонового излучения с неизвестными статистическими характеристика в робастном алгоритме восстановления изображения неизвестного объекта [6].
Рисунок 1. Изображения исходного зашумленного круга и результатов его фильтрации медианными фильтрами.
Вычисленные показатели качества изображений приведены в следующей таблице.
Таблица 1.
Показатели качества изображений
|
Изображения |
I | w0 | w1 | µ |
Коэф |
| Исходное | 6.412 | 131.297 | 1029.734 | 0.149 | 1.008 |
| Фильтр 3-о порядка | 5.566 | 27.441 | 586.305 | 0.253 | 2.217 |
| Фильтр 5-о порядка | 5.182 | 13.545 | 438.322 | 0.273 | 2.802 |
| Фильтр 7-о порядка | 5.020 | 10.390 | 425.414 | 0.244 | 3.806 |
В последнем столбце таблице приведён коэффициент растяжения значимого интервала интенсивности изображения к максимально возможному. Анализ приведённых данных показывает, что поведение показателя топографии более точно характеризует структуру анализируемого изображения, чем обычно используемой показатель информативности. Визуальное восприятие приведённых на рисунке изображений существенно различается, а значения показателя I изменяется на ~ 20%, в то время как показателя – в w0 ~ 12 раз. Это обстоятельство существенно при решении задачи сегментации малоконтрастного изображения, когда ограничиваются выделением на изображении неизвестного объекта небольшого числа сегментов. При решении этой задачи целесообразно проводить анализ характеристик поведения показателей качества как функций уровней интенсивности, которые представлены на рисунке 2.
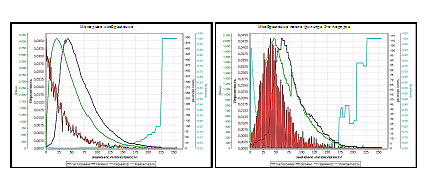
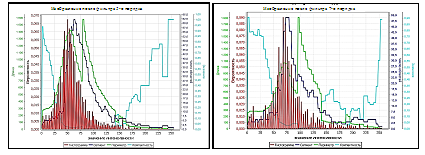
Рисунок 2. Характеристики поведения показателей качества.
На рисунках красным цветом приведена гистограмма изображения, синим – характеристика поведения показателя топологии, зеленым – показателя метрики, голубым – показателя компактности, а также проведено масштабирование интервалов изменения значений характеристик к единому интервалу изменения условных экранных координат. Анализ поведения приведенных зависимостей показывает, что задачу сегментации малоконтрастных изображений целесообразно решать в области изменения интенсивностей, расположенных справа от значения, связанного с глобальным максимумом векторов . При этом для выделения области локализации изображения информационного объекта использовать критерий 1-о локального максимума показателя компактности [6].
Заключение
В работе предложен набор показателей качества малоконтрастного цифрового изображения и связанных с ними характеристик поведения как функций уровней интенсивности, которые позволяют оценить пространственную сложность изображения на плоскости и его информативность.
Приведён пример поведения предложенных показателей и характеристик при проведении медианной фильтрации изображений эталонного объекта в условиях сложной фоновой обстановки с использованием фильтров разного порядка.
Список литературы
- Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. М.: Наука, 1979. – 285 с.
- Василенко Г. И. Голографическое распознавание образов. М.: Сов. радио, 1977 – 328 с.
- Т.С. Хуанг, Дж. О. Эклунд, Г. Дж. Нуссбаумер и др. Быстрые алгоритмы в цифровой обработке изображений. Под редакцией Т.С. Хуанга: Пер. с англ.-М. Радио и связь, 1984 – 224с.
- Новые методы обработки изображений. Под ред. А.А. Потапова. – М.; ФИЗМАТЛИТ, 2008. – 496с. – ISBN 978-5-9221-0844-6
- Chochia P. A. A pyramidal image segmentation algorithm. Journ. Commun. Technol. Electron. 55, N 12, 2010. – 1550–1560 p.
- Лавров В.В., Прохоров М.Е., Тюрин В.С., Шигаев А.К. Робастный алгоритм восстановления изображения объекта в системе атмосферного видения. Материалы XIV Международной научно-практической конференции «Актуальные вопросы развития инновационной деятельности в новом тысячелетии». ISSN 3478-3215s. Ежемесячный научный журнал Международного независимого института Математики и Систем №3(14), 2015. – 33–36 с.
- Тартаковский Г. П. Теория информационных систем. ISBN 5-89155-136-5. М.: Физматкнига, 2005. – 304с.
- Milyukova O.P. On Justification of Image Model. Optical Information Science and Technology (OIST97) Proc. SPIE, vol. 3348, 1997. 283–289 p.
- Кронрод А.С. О функциях двух переменных. УМН, т. 5, вып. 1(35), 1955. 24–134 с.[schema type=»book» name=»ХАРАКТЕРИСТИКИ КАЧЕСТВА МАЛОКОНТРАСТНЫХ ЦИФРОВЫХ ИЗОБРАЖЕНИЙ НЕИЗВЕСТНОГО ОБЪЕКТА» description=»Предлагается ряд интегральных показателей качества и характеристик их поведения как функций уровней интенсивности цифровых малоконтрастных изображений, которые позволяют оценивать анализируемые изображения. Приводится пример анализа результатов обработки малоконтрастного изображения медианными фильтрами разного порядка в составе разработанных робастных алгоритмов фильтрации.» author=»Лавров Василий Васильевич, Рындин Юрий Георгиевич, Тюрин Владимир Семёнович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2016-12-22″ edition=»euroasian-science.ru_25-26.03.2016_3(24)» ebook=»yes» ]

