Введение. Форма значительного числа окружающих нас объектов случайна. Примерами случайных изображений могут быть изображения органов человека, облачности, листьев деревьев, пламени, профиля лица человека и т.п. Существенная вариабельность формы изображений со случайными контурами не позволяет рассматривать их как зашумленные изображения некоторых эталонных объектов. Тем не менее, человек достаточно уверенно отличает их друг от друга и успешно распознает такие объекты [1].
Традиционно задача распознавания изображений решается на основе процедуры пространственной корреляции. Этот подход неизбежно связан со следующими недостатками: чувствительностью алгоритмов к изменению масштаба и взаимной угловой ориентации совмещаемых изображений, а также с обработкой большого количества (а часто и всех) точек совмещаемых изображений. Если параметры угла поворота и масштаба произвольны и неизвестны, то при распознавании изображений требуется перебор с небольшим шагом значений каждой комбинации этих параметров, что приводит к значительным временным затратам.
Перспективным видится подход к решению данной задачи на основе метода контурного анализа. Этот метод использует всю информацию, имеющуюся в контурах изображений, и инвариантен к параметрам линейных преобразований. Из-за небольшого, по сравнению со всеми изображениями, количества контурных точек, временные затраты при этом снижаются.
Для решения задачи распознавания используют полиномиальную и Марковскую модели случайных контуров. Первая из них предполагает независимость ЭВ контура и известную вероятность появления каждого из них. Во втором случае устанавливается зависимость между случайными величинами . При этом изменение масштаба и (или) угла поворота приводит к изменению размерности контура и, как следствие, к зависимости элементов матрицы вероятностей переходов от параметров этих преобразований [1].
Также для распознавания изображений применяют метод активного контура. Активный контур представляет собой набор точек, находящихся в одном шаге от объекта, которые меняют свое местоположение, пока все точки не будут лежать на границе объекта. Данный метод чувствителен к перепаду яркости на изображении, поэтому границы объекта должны быть достаточно четкими [2].
Целью данной работы является формирование обобщенной модели контура случайной формы.
Статистическая модель контура случайной формы и ее числовые характеристики.



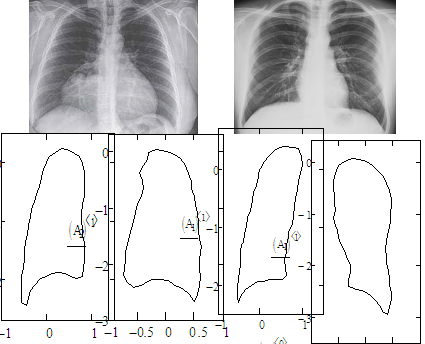
Рис. 1. Пример реализации случайного контура
Корреляционная функция комплексной случайной функции — это неслучайная функция двух независимых аргументов и , значение которой при каждой паре фиксированных значений аргументов равно корреляционному моменту сечений, соответствующих этим же фиксированным значениям аргументов:
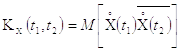
Нормированной корреляционной функцией случайной функции называют неслучайную функцию двух независимых переменных и , значение которой при каждой паре фиксированных значений аргументов равно коэффициенту корреляции сечений, соответствующих этим же фиксированным значениям аргументов:
[4].

Формирование общей модели контура случайной формы. Исходными данными для получения статистической модели случайного контура являются контуры левого и правого легкого, представленные на рисунке 2.
Рассчитаем для данных контуров математическое ожидание отдельно для левого и правого легкого. Математическое ожидание контуров представлено на рисунке 3.
Произведем расчет ковариационной матрицы, найдем ее собственные значения λ:
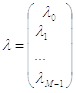 ,
,
и их относительное процентное содержание ОПС отдельно для правого и левого легкого.
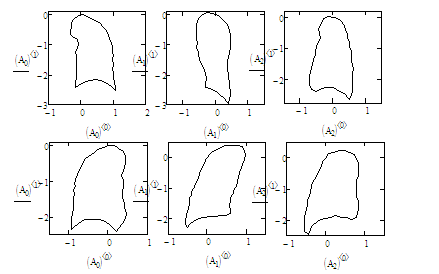
Рис. 2. Контуры левого и правого легкого
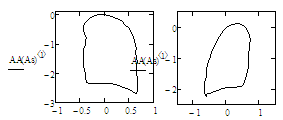
Рис. 3. Математическое ожидание левого и правого легкого
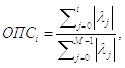
где M – количество точек, с помощью которых представлены исходные контуры.Относительное процентное содержание определяется по формуле:
Значения, полученные при расчете собственных значений и их относительного процентного содержания, представлены ниже.

По рассчитанным значениям относительного процентного содержания, выбираем столько первых собственных значений, которые описывают наибольшую часть дисперсии, например, 99% всей дисперсии (можно при необходимости взять все собственные значения). Для этих первых значений рассчитываем собственных векторов ковариационной матрицы, которые сводим в таблицу и получаем общую модель контура случайной формы.
Изменяя значения элементов вектора, который задает параметры для формирования модели случайного контура, можно получать наборы различных контуров случайной формы, которые представлены в таблице 1.
Заключение. Рассмотренный способ формирования общей модели контура случайной формы позволяет сгенерировать множество отличных друг от друга контуров, которые принадлежат к одному классу, о чем свидетельствуют приведенные примеры. Данный способ может быть применен для различных задач распознавания изображений, в частности, его можно использовать для создания базы данных.
Таблица 1
Контуры случайной формы
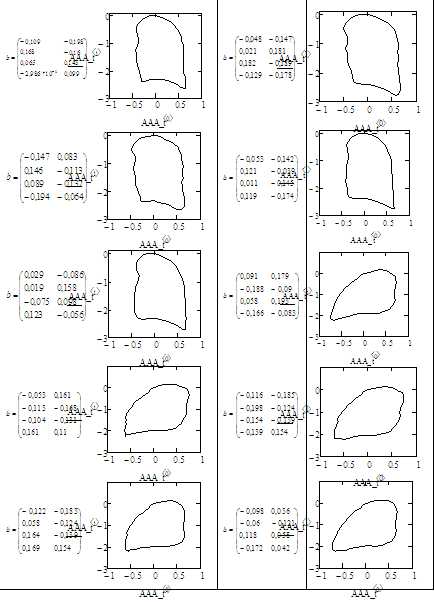
Список литературы:
- Введение в контурный анализ и его приложение к обработке изображений и сигналов/ Под ред. Я.А. Фурмана. – М.: ФИЗМАТЛИТ, 2002. – 592 с.
- Дегтярева А.А. Деформируемые модели // Компьютерная графика и мультимедиа. Выпуск №3(2)/2005. URL: https://cgm.computergraphics.tu/content/view/75
- Хафизов, Р.Г. Статистическая модель изображений со случайной формой / Р.Г. Хафизов, А. М. Суслова, Т. П. Киселева // Сборник материалов XI международной научно-технической конференции «Оптико-электронные приборы и устройства в системах распознавания образов, обработки изображений и символьной информации» (Распознавание — 2013). – Курск, 2013. – С. 112-115
- Хафизов Р.Г. Распознавание изображений со случайной формой / Р.Г. Хафизов, Т.В. Яранцева, Т.П. Киселева, А.М. Суслова // Научно-технический журнал «Вестник Поволжского государственного технологического университета». – Йошкар-Ола: ПГТУ, 2013. с. 52-60.[schema type=»book» name=»ФОРМИРОВАНИЕ ОБОБЩЕННОЙ МОДЕЛИ КОНТУРА СЛУЧАЙНОЙ ФОРМЫ» description=»Рассмотрен подход к формированию модели контура изображения со случайной формой. При этом контур представлен как комплексная случайная функция, заданная совокупностью возможных реализаций. Предложена обобщенная модель случайного контура, учитывающая форму изображения и ее корреляционные свойства.» author=»Яранцева Татьяна Валентиновна, Суслова Анастасия Михайловна, Хафизов Ринат Гафиятуллович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-18″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_28.11.15_11(20)» ebook=»yes» ]

