Теория линейных систем является наиболее развитым разделом теории автоматического управления в силу того, что использование принципа суперпозиции позволяет применять удобный аппарат передаточных функций и пространства состояний. Между тем, реальные объекты управления могут обнаруживать значительные нелинейные свойства, что должно учитываться при проектировании систем управления ими. Ниже рассмотрен подход к проектированию нелинейных регуляторов, основанный на представлении регулятора как нейросетевой структуры, в которой настраиваются нелинейные активационные функции.
Вначале рассмотрим традиционные линейные регуляторы по отклонению. На практике наиболее распространены ПИД-регуляторы, настраиваемые во временной или частотной области [1, 2].
Закон управления ПИД- регулятора, представляющего собой частный случай линейного корректирующего звена, описывается формулой
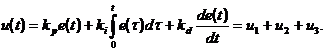(1)
Для случая ПД- или ПИ- регулятора возможна наглядная геометрическая интерпретация закона управления, поскольку в этом случае управляющая поверхность представляет собой плоскость (рис. 1).
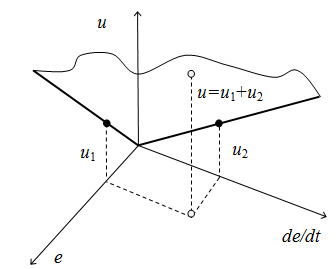
Рисунок 1. Пропорционально-дифференциальное управление
Таким образом, как показывает (1), закон управления состоит из 3-х формально независимых компонент, связь которых неявно определяется целью управления.
На рис. 2 приведена типовая структура системы управления по состоянию (где A, B, C и K – матрицы объекта, входа, выхода и обратной связи соответственно, X, Y и g – вектор состояния, выходной сигнал и уставка).
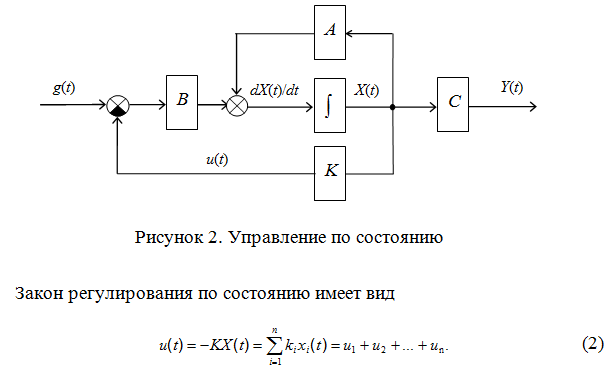
где X – вектор состояния, n – порядок объекта.
На основании (1) и (2) можно сделать два вывода:
- Произвольный линейный закон управления описывается гиперплоскостью в n-мерном пространстве (где n – порядок объекта управления).
- Описание управляющей гиперплоскости формируется как сумма законов управления для каждого измерения в отдельности.
Рассмотрим далее нелинейные законы управления, которые могут быть реализованы с помощью нейросетевых и нечетких логических регуляторов (НЛР) [3 — 6].
Заметим, что линейный ПИД-регулятор может быть описан с помощью одного нейрона с линейной активационной функцией, в котором веса входов соответствуют коэффициентам kp, ki и kd.
Многослойная нейронная сеть является универсальным аппроксиматором, но для этого ее нейроны должны использовать нелинейные активационные функции. Например, для реализации нелинейного закона управления с помощью 2-х слойной нейронной сети нейроны 1-го слоя должны иметь нелинейную активационную функцию (например – гиперболический тангенс), а нейроны 2-го слоя – линейную активационную функцию (рис. 3).
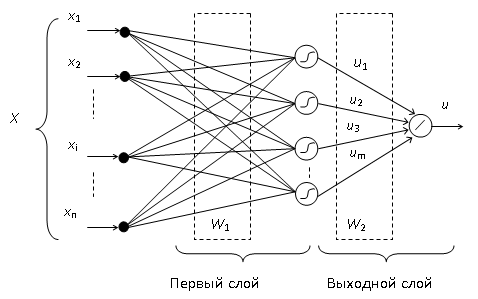
Рисунок 3. Двухслойная нейронная сеть прямого распространения
В соответствии с рис. 3 можно описать закон управления формулой:
(3)
где f – нелинейная активационная функция.
При нейросетевой реализации дискретного ПИД-регулятора получаем структуру, приведенную на рис. 4.
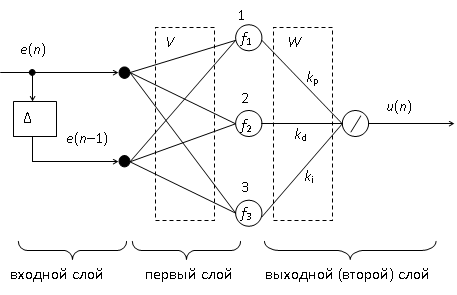
Рисунок 4. Нейросетевой вариант регулятора ПИД-типа
Работа регулятора определяется активационными функциями нейронов f1, f2, f3. Если эти функции линейные, то получается линейный ПИД-регулятор. Поведение регулятора может быть оптимизировано при использовании настраиваемых нелинейных активационных функций [7].
Нечеткий регулятор ПИД-типа можно представить структурой, показанной на рис. 5 (где N и DN – коэффициенты нормализации и денормализации).
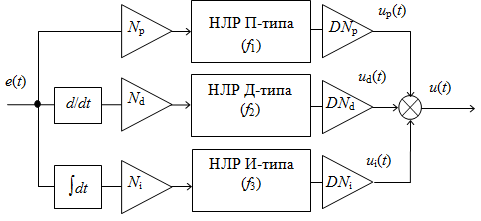
Рисунок 5. Декомпозиция НЛР ПИД-типа
Сравнивая рис. 4 и 5, можно заметить две особенности:
- Структура рис. 5 напоминает нейронную сеть, и НЛР в каждом из каналов выполняет роль активационной функции.
- Коэффициенты денормализации могут быть выбраны равными коэффициентам линейного ПИД-регулятора.
По каждому из 3-х каналов с помощью НЛР обеспечивается некоторое нелинейное преобразование, пример которого приведен на рис. 6.
В правой части рис. 6 показана управляющая кривая, которая играет ту же роль, что и активационная функция на рис. 4. Изменяя количество термов, можно получить любой вид управляющей кривой.
На основании (3) и рис. 4 -6 можно сделать следующие выводы:
- Произвольный нелинейный закон управления описывается гипероверхностью в n-мерном пространстве.
- Описание управляющей гиперповерхности формируется как сумма нелинейных законов управления для каждого измерения в отдельности.
- Настройка нелинейного нечеткого регулятора равноценна оптимизации параметров нелинейной активационной функции.
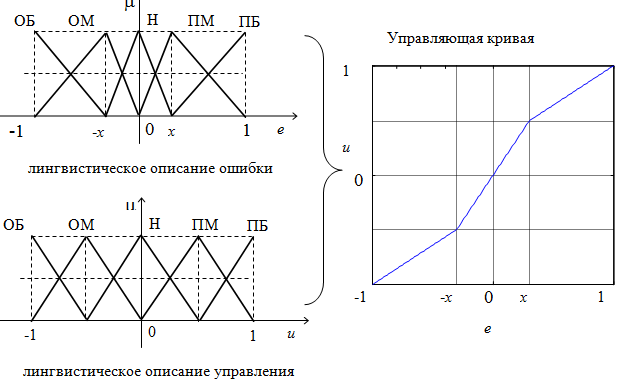Рисунок 6. Геометрическая интерпретация закона управления
При оптимизации линейного закона управления вида (1) или (2) параметры представлены набором констант, где одна константа соответствует одному каналу управления.
При оптимизации нелинейного закона управления одному каналу будет соответствовать целый набор констант P = {p1, p2,…,pk}. Целевая функция может быть выбрана в виде:
(4)
где y и y* — реальное и желаемое значение выхода объекта, i –момент времени.
На рис. 7 показана общая схема оптимизации в режиме off line.
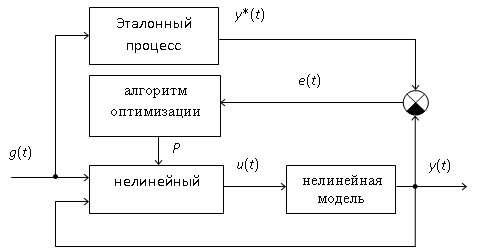
Рисунок 7. Обучение нелинейного регулятора
Целевая функция является (4) мультимодальной, что требует использования методов глобальной оптимизации, таких как генетический алгоритм [8].
Для упрощения задачи глобальной оптимизации в ряде случаев может быть использован следующий алгоритм [9, 10]:
- Синтезируется линейный ПИД–регулятор (линейная нейросеть), параметры которого kP, ki, kd, будут играть роль коэффициентов денормализации.
- Настраиваются нелинейные функциональные зависимости, описывающие нечеткий закон управления (активационные функции) по каждой из входных переменных.
Этот алгоритм был использован при управлении активной подвеской транспортного средства [7], нелинейными объектами типа Гаммерштейна и Винера [11], нелинейным осциллятором [9]. Приведенные в этих работах примеры моделирования показывают, что использование нелинейных регуляторов может обеспечить значительное уменьшение времени переходных процессов и сокращение перерегулирования, которое недостижимо при линейном законе управления.
Таким образом, предлагаемый подход может быть полезен при модернизации систем управления широким классом динамических объектов, где используются линейные ПИД-регуляторы.
Список литературы:
- Astrom K.J., Hagglund T. Advanced PID control. ISA (The Instrumentation, System, and Automation Society), 2006. 460 p.
- Олссон Г., Пьяни Дж. Цифровые системы автоматизации и управления. СПб, 2001. 577 с.
- Бураков М.В. Синтез нейронного регулятора // Изв. Академии наук. Теория и системы управления, 1999, №3, С.140-145.
- Бураков М.В., Коновалов А.С. Синтез нечетких логических регуляторов // Информационно-управляющие системы, №1, 2011г., с.14-19.
- Бураков, М.В. Нечеткие регуляторы / М. В. Бураков; ГУАП. СПб., 2010 г. 237с.
- Бураков М.В. Нейронные сети и нейроконтроллеры // СПб: ГУАП, 2013г. 284с.
- Бураков М.В. Нейросетевая реализация ПИД-регулятора // XVI Всероссийская НТК «Нейроинформатика-2014». Сборник научных трудов. В 3-х частях. Ч. 3. М.: НИЯУ МИФИ, 2014. С.117-125.
- Бураков, М.В. Генетический алгоритм: теория и практика. / М.В. Бураков; ГУАП. СПб, 2008. 164с.
- Бураков М.В., Кирпичников А.П. Нечеткий регулятор ПИД-типа для нелинейного объекта // Вестник Казанского технологического университета. 2015. Т.18, №4, с. 242-244.
- Бураков М.В., Кирпичников А.П. Синтез дискретного нейро-пид регулятора // Вестник Казанского технологического университета. 2014. Т.17, №1, с. 286-288.
- Бураков М.В. Нелинейные ПИД-регуляторы для управления электроприводом // Труды VI Всероссийской научно-практической конференции «Автоматизированный электропривод и промышленная электроника (АЭПЭ 2014)», С.12-17.[schema type=»book» name=»СИНТЕЗ НЕЛИНЕЙНЫХ РЕГУЛЯТОРОВ» description=»В статье представлен двухшаговый алгоритм проектирования нелинейного регулятора для динамического объекта. На первом шаге искусственная нейронная сеть используется для реализации линейного ПИД-регулятора. На втором шаге происходит настройка нелинейных активационных нейронов функций с помощью генетического алгоритма. Предлагаемая методология проверена компьютерным моделированием.» author=»Бураков Михаил Владимирович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-02″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_27.06.2015_06(15)» ebook=»yes» ]