В настоящее время проведены многочисленные исследования вязкоупругих свойств текстильных материалов. Однако разнообразие материалов требует разработки новых методов исследования их деформационных свойств. Изготовление различных материалов на основе текстильного сырья оказывает существенное влияние на их вязкоупругие свойства, что обосновывает разработку новых математических моделей, с применением компьютерных методов обработки экспериментальных результатов, позволяющих создание новых методов анализа механических свойств и более достоверно прогнозировать деформационные процессы.
Установлено, что совершенствование методов анализа и обработки экспериментальных результатов на основе математического моделирования позволяет моделировать в лабораторных условиях воздействия, испытываемые материалами при их переработке и в процессе эксплуатации.
Такие сложные явления, как релаксационные, можно описать, используя, как показал опыт изучения аналогичных явлений в полимерных материалах, метод моделирования [1]. Правильный выбор модели позволяет глубже изучить закономерности деформации текстильных материалов и предсказать их поведения при определенных условиях эксплуатации. Модельный метод изучения релаксационных процессов в полимерных материалах можно считать достаточно разработанным, то применительно к текстильным материалам изучения находится на начальном этапе.
Проведенные исследования механических свойств текстильных материалов и изделий из них требует разработку математических моделей деформационных свойств на основе простых релаксационных функций. При этом необходимо требовать минимизации количества параметров математической модели и их адекватность. При этом важным является выбор интегральных ядер. К настоящему времени предложено много различных ядер. Преимущества того или иного ядра зависят от физических свойств материала и вида решаемой задачи. Наиболее приемлемыми являются ядра Абеля, Работнова, Ржаницына, Колтунова [2]. Однако указанные типы ядер обладают линейными свойствами. Основные требования при динамических расчетах для текстильных материалов приводит к необходимости учета нелинейных свойств. Так как с ростом напряжений почти для всех текстильных материалов наблюдается отклонение от линейной теории наследственности.
В [2] создана общая нелинейная теория наследственной теории вязкоупругости, в которой применяется принцип обращения нелинейных операторов для получения обратных соотношений междуи предложены методы решения задач линейной и нелинейной теории термовязкоупругости, рассмотрены задачи динамики и прочности.
Предложенный вариант математического моделирования целесообразно для прогнозирования деформационных процессов в текстильных материалах.
В качестве примера определения механических характеристик текстильных материалов приведем обработку экспериментальных данных по релаксации и ползучести хлопчатобумажной нити 56 текс. На рис.1 видно, что кривые релаксации, полученные при различных значениях деформации, параллельным сдвигом вдоль логарифмической шкалы времени на величину
Используя математическую модель релаксации (1), по экспериментальным кривым релаксации (рис.1) можно найти характеристики процесса релаксации [3], которые в дальнейшим используется для прогнозирования деформационных процессов. Аналогично по экспериментальным кривым ползучести (рис.2.) определяются параметры ползучести [4].

Рис.1. Процесс деформирования для хлопчатобумажной нити с линейной плотностью
(t1=1 мин, снятие нагрузки при t=10 мин, σ = 136 МПа): точки – экспериментальные данные; линия – апроксимационная кривая.
Прогнозирование деформационных процессов текстильных материалов проводится на основе известных интегральных соотношений Больцмана -Вольтера для процессов нелинейно-наследственной релаксации и нелинейно-наследственной ползучести соответственно [3]:
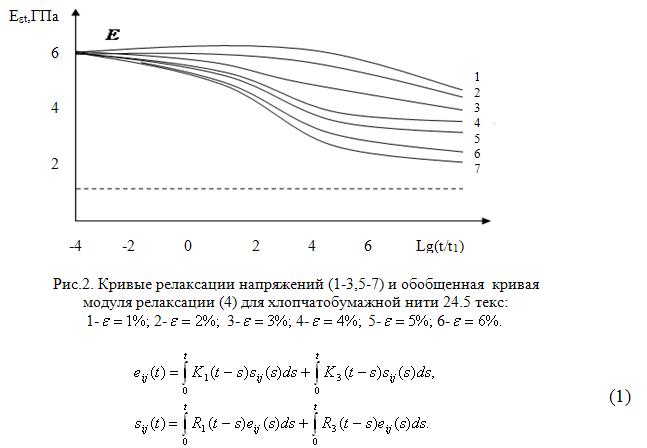
Применения для моделирования деформационных процессов интегральных соотношений (1) позволяет расширить области доверительного прогнозирования. Результаты расчета для хлопчатобумажной нити 24.5 текс приведены на рис.3. Видно, что результаты расчетов хорошо согласуются с экспериментальными данными.
Таким образом, в работе предложено методика анализа деформационных свойств текстильных материалов на основе математической модели с нелинейно-вязкоупругими свойствами, позволяющей увеличить диапазоны времени, нагрузки и деформации.
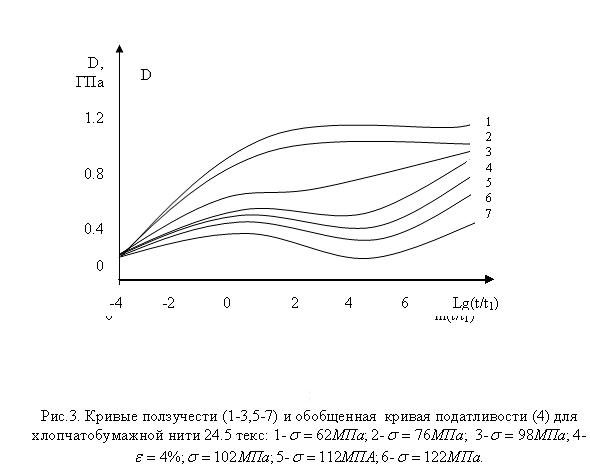
Рис.3. Кривые ползучести (1-3,5-7) и обобщенная кривая податливости (4) для хлопчатобумажной нити 24.5 текс: 1-2- 3-4-5-6-
Разработана методика определения вязкоупругих характеристик, по результатам испытаний образцов в простых режимах релаксации и ползучести.
- Демидов А.В., Макаров А.Г., Сталевич А.М. Вариант прогнозирования нелинейно-наследственной вязкоупругости полимеров. Прикладная механика и техническая физика, 2007. Т.48, №6.
- Ильюшин А.А., Победря Б.Е., Основы математической теории термовязкоупругости, М.: Наука, 1970.-280 с.
- Колтунов М.А., Ползучесть и релаксация.-М.: Высшая школа, 1976.-277 с.
- Абдиева Г.Б., Мавланов Т. Определение демпфирующих свойств текстильных материалов. Проблемы текстиля. 2006. №3. 80-82 с.[schema type=»book» name=»ПРОГНОЗИРОВАНИЕ НЕЛИНЕЙНО-НАСЛЕДСТВЕННОЙ ВЯЗКОУПРУГОСТИ ТЕКСТИЛЬНЫХ МАТЕРИАЛОВ» description=»Основной целью выполнения данной работе является разработка математической модели с применением наследственной нелинейной теории вязкопругости и прогнозирования нелинейной вязкоупругости текстильных материалов на основе предлагаемой модели по кривым ползучести и релаксации. » author=»Абдиева Гулара Бабаниязовна, Ярашов Жавлан Адамбаевич, Мавланов Тулкин» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-12″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.05.2015_05(14)» ebook=»yes» ]

