Интенсификация технологических процессов, связанных с течением жидкостей, часто напрямую зависит от решения проблемы кавитации – эволюции разрывных потоков в условия пониженного давления в некоторой области движения жидкостной среды вследствие достижения значительных скоростей (гидродинамической кавитации) или действия акустических волн (акустической). Эффективность проектирования оборудования специального назначения в соответствии с системно-структурным анализом определяется теоретическими основами [8, 12] рассматриваемого процесса.
В настоящем изложении бóльшее внимание уделяется существующим математическим моделям в задачах первого вида кавитации. Заметим, что согласно экспериментальным данным это явление наблюдается, если статическое давление в некоторой области течения жидкости падает до значений насыщенного пара [3, с. 243; 4, с. 525]. Значение радиуса образовавшихся полостей (пузырей) зависит от степени содержания газа в составе заполняющей их системы пар-газ. Чем меньше газа находится в объеме пузыря, тем быстрее происходит его схлопывание, которое сопровождается достижением температуры газа порядка 103 0С и его давления до 102 МПа. Способность жидкостных течений к разрыву существенно повышается с увеличением их степени неоднородности или при обтекании шероховатых тел, что приводит к возникновению эрозии поверхностей последних.
Для характеристики механизма поведения кавитационных потоков используются различные показатели, например, число кавитации [8, с. 63] без учета сил тяжести и добавочное число кавитации [1, с. 81] в режиме суперкавитации (дополнительной подачи газа для предотвращения схлопывания пузырьков)

При этом основными задачами исследования, как правило, являются следующие: выявление механизма образования пузыря [3, 7, 14], условий его роста [14], сжатия [3, 12] и схлопывания [5, 15, 17], изучение физических свойств жидкостной среды [7], режимы осуществления суперкавитации [1, 10], моделирование разрывных течений жидкости при обтекании тел различной формы [1, 13, 10] и т.п.
Соответствующий анализ литературных источников выявил два основных подхода к математическому описанию процесса формирования кавитационных потоков в средах различной природы – стохастический и детерминированный.



Акустической кавитации посвящена также работа [11], в которой рассматриваются условия сжатия парового пузыря с учетом его несферического возмущения формы, вязкости жидкостной среды, неоднородного характера изменения давлений, плотности пара.
При переменной вязкости жидкостной среды в работе [7] для стадий развития кавитации и роста пузырей в вулканической магме предлагается использовать ИКВ-модель [5, 15, 17, 12] при замене уравнения Эйлера уравнением Навье – Стокса. При этом уравнения сохранения и Рэлея типа (7) дополняются кинетическими уравнениями, в том числе, диффузии. Дальнейшая дегазация изучаемой вязкой среды приводит к резкому росту значения вязкости, что значительно упрощает модель, исключая уравнение Рэлея при возрастании роли диффузионных эффектов [7].
Исследования кавитационных эффектов в клапанных щелях выявили при резком падении давления (от 14 МПа до 610 Па) возможную сублимацию, когда пузыри эмульсии, образовавшиеся в зоне «кипения» покрываются затвердевшим слоем и при соударениях с потоком других пузырей разрушают их, ускоряя процесс эрозии щелевых поверхностей [9]. В этом случае также применяется уравнение типа Эйлера в сочетании с гипотезой дискретности жидкой фазы
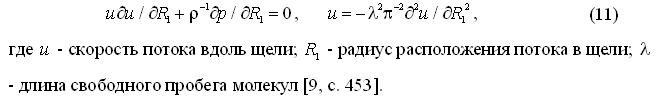
Вопросы обтекания препятствий кавитационными потоками в условиях суперкавитации связаны с задачами оптимизации формы сопла, кавитаторов для управления размерами каверны и ее сопротивлением [10, с. 35]. Например, такие постановки имеют решения, получаемые на основе вариационных принципов конформных отображений [10] или с помощью программных продуктов типа ANSYS в процессе подбора границы расчетной области согласно заданным значениям давлений при интегрировании уравнений течения газа [1].
Таким образом, разнообразие математических моделей течения кавитационных потоков объясняется широким спектром проблемных технологических задач. В основном рассматривается механизм эволюционного поведения одиночного кавитационного пузыря, т.е. его движение, рост, сжатие и схлопывание на основе системы гидродинамических уравнений. Процесс образования потока кавитирующих пузырей требует стохастической постановки задачи. Кроме того, усложнение характеристик физических свойств жидкостной среды, например, переменность ее вязкости, приводит к комбинированным моделям, сочетающим методы гидродинамики и построение кинетических уравнений. Многофакторная постановка задачи оптимизации конструктивно-режимных параметров оборудования специального назначения с возможной реализацией процесса кавитации вынуждает в расчетах использовать готовые программные продукты типа ANSYS.
Список литературы
- Варюхин А.Н. Деформация границ осесимметричной каверны газовыми струями // Приклад. механика и техн. физика. 2008. Т. 49., № 5. С. 80-86.
- Давыдов М.Н., Кедринский В.К. О механизме формирования кавитирующих потоков // Приклад. механика и техн. физика. 2008. Т. 49. С. 65-73.
- Запорожец Е.П., Холпанов Л.П., Зиберт Г.К., Артемов А.В. Исследование вихревых и кавитационных потоков в гидравлических системах // Теор. осн. хим. технол. 2004. Т.38, № 3. С. 243-252.
- Зельдович Я.Б. К теории образования новой фазы. Кавитация // Журн. эксперим. и теорет. физики. 1942. Т.11/12. С.525-538.
- Иорданский С.В. Об уравнениях движения жидкости, содержащей пузырьки газа // Приклад. механика и техн. физика. 1960. №. 3. С. 102-110.
- Кедринский В.К. Динамика зоны кавитации при подводном подрыве вблизи свободной поверхности // Приклад. механика и техн. физика. 1975. № 5. С. 68-78.
- Кедринский В.К. О газодинамических признаках взрывных извержений вулканов. 1. Гидродинамические аналоги предвзрывного состояния вулканов, динамика состояния трехфазной магмы в волнах декомпрессии // Приклад. механика и техн. физика. 2008. Т. 49, 6. С. 3-12.
- Кнепп Р., Дейли Дж., Хэммит Ф. Кавитация. М.: Мир, 1974. – 668 с.
- Куленко В.Г., Фиалкова Е.А., Баронов В.И. Гидро- и термодинамика субкавитационного дробления эмульсий в клапанной щели гомогенизатора // Теор. осн. хим. технол. 2009. Т.43, № 4. С. 452-458.
- Монахов В.Н., Губкина Е.В. Оптимизация форм препятствий, обтекаемых с отрывом струй // Приклад. механика и техн. физика. 2007. Т. 48, № 3. С. 30-39.
- Нигматулин Р.И., Аганин А.А., Ильгамов М.А., Топорков Д.Ю. Эволюция возмущений сферичности парового пузырька при его сверхсжатии // Приклад. механика и техн. физика. 2014. Т. 55, № 3. С. 82-102.
- Пирсол И. Кавитация. М.: Мир, 1975. – 95 с.
- Промтов М.А. Машины и аппараты с импульсными энергетическими воздействиями на обрабатываемые вещества: учебное пособие. М.: Машиностроение-1, 2004. 136 с.
- Уткин А.В. Влияние кинетики разрушения материалов на амплитуду откольного импульса // Приклад. механика и техн. физика. 2011. Т. 52, № 1. С. 185-1193.
- Когарко Б.С. Об общей модели кавитирующей жидкости // Докл. АН СССР. 1961. Т. 137, № 6. С. 1331-1333.
- Raleigh J.C. On the pressure developed in a liquid during the collapse of a spherical cavity // Phil. Mag. 1917. V. 34. P. 94-98.
- Van Wijngaarden L. On the collective collapse of a large number of cavitation bubbles in water // Proc. of 11th Intern. congress of appl. mech., Munich (Germany), Aug. 1964. Berlin: Springer-Verlag, 1964. P. 854-861.[schema type=»book» name=»О СПОСОБАХ ОПИСАНИЯ ПРОЦЕССА ФОРМИРОВАНИЯ КАВИТАЦИОННЫХ ПОТОКОВ» description=»Целью настоящей работы является обзор существующих способов математического описания процесса формирования кавитационных потоков в средах различной природы. Соответствующий анализ литературных источников выявил два основных подхода к указанной проблеме – стохастический и детерминированный. Целесообразность их применения зависит от стадии кавитации, в частности, образование кавитирующих пузырей описывается кинетическими уравнениями, а этапы развития данного процесса и роста пузырей – в рамках гидродинамики.» author=»Капранова Анна Борисовна, Солопов Сергей Александрович, Мельцер Александр Михайлович» publisher=»Басаранович Екатерина» pubdate=»2017-03-03″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_27.06.2015_06(15)» ebook=»yes» ]

