Идентификация опасностей, возникающих при осуществлении производственной деятельности осуществляется в процессе контролирующей деятельности [1].
Основными видами контроля являются:
— оперативный со стороны руководителей работ и других должностных лиц;
— выполняемый службой охраны труда в силу должностных обязанностей работников этой службы;
-производственный, выполняемый службой промышленной безопасности;
— административно — общественный (трехступенчатый).
Контроль как функция социального управления людьми представляет собой систему проверки соответствия объекта контроля, принятым управленческим решениям – законам, нормам, стандартам и т.д. оценивая результаты воздействия на объект и отклонений от принятых управленческих решений.
Конкретными объектами контроля являются такие элементы управляемой системы и характеристики объектов управления, которые обеспечивают безопасность работающего, исправность машин и прочие параметры обеспечения безопасности. Основными функциями контроля являются:
— анализа, необходимую для выявления ключевых параметров внешней и внутренней среды на безопасность деятельности;
— планирования, заключающейся в разработке системы показателей для позиционирования производства в области обеспечения безопасности;
— учета, для стратегического и управленческого учета показателей безопасности;
— организации, для разработки поддержки принятия управленческих решений в области обеспечения безопасности;
— контроля за процессом достижения заданных целей путем выявления контролируемых показателей от нормируемых по местам их возникновения, причинам и виновника.
Основные задачи, решаемые системой контроля приведены на рисунке.
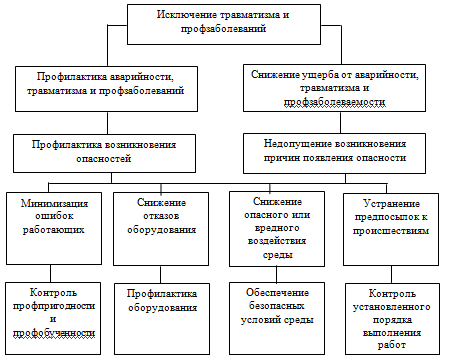
Рисунок. Основные задачи системы контроля за состоянием безопасности производства
Совершенствование контрольно-профилактической работы идет по следующим направлениям.
- Обоснование объема выборки периодически проверяемых производственных объектов.
- Разработка план – графиков их обследования органами контроля.
- Оценка эффективности альтернативных воздействий, предложенных в ходе проверки для предупреждения происшествий и профессиональных заболеваний.
Обоснование объема и состава инспектируемых объектов обусловлено невозможностью систематически и качественно проверять одновременно все производственные объекты. Каждый из них может быть обследован на продолжительных интервалах времени, однако при этом не будет выдержано требование к оперативности управления безопасностью. Для повышения эффективности контрольно-профилактической работы в этих условиях приходится проводить выборочный контроль лишь некоторых из них.
Обоснование выборки обследуемых объектов наиболее целесообразно осуществлять при использовании в качестве критерия оптимизации информацию о происшествиях и предпосылок к ним. В первую очередь необходимо планировать те объекты, где максимальное число происшествий.
Ограничением к объему выборки запланированных для обследования объектов должны служить трудозатраты.
В предположении о пропорциональности указанных трудозатрат, а также – числу зарегистрированных на них происшествий и предпосылок к ним хi(τ), рассматриваемая задача сводится к определению такого состава выборки обследуемых производственных объектов, при котором обеспечивается получение максимально возможной информации об обстоятельствах появления, и требуемые для ее сбора и изучения, трудозатраты – не превышают выделенных на эти цели. Математически, задача составления плана контрольно-профилактической работы состоит в определении таких m объектов из N, при которых соблюдаются следующие, более строгие условия:
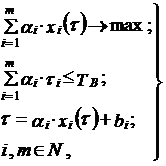
где m, N – число выбранных и количество проверяемых производственных объектов соответственно;
αi – булева переменная (параметр, равный единице для объектов из подмножества m и равный нулю для других объектов);
аi, bi – постоянные, пропорциональные времени, необходимому для изучения обстоятельств возникновения одного происшествия и для исследования к i-ому объекту, соответственно;
TB – трудозатраты, для инспектирования объектов в рассматриваемом периоде времени.
Рассматриваемая задача принадлежит к классу задач линейного (комбинаторного) программирования. Способом ее решения может служить алгоритм Колесара [2], основанный на методе ветвей и границ. Выбор данного алгоритма обусловлен его эффективностью для задач с достаточно большой размерностью оптимизируемых параметров.
Качество контроля характеризуется вероятностными параметрами осуществляемых преобразований. При этом, под вероятностными P(H) (yiǀxk) подразумеваются ошибки первого и второго рода – k01, k10; их дополнения до единицы k11, k00; условные вероятности устранения обнаруженных предположений – Pky, а под ресурсами – τ(yiǀxk), необходимыми для операционного контроля и устранения обнаруженных отклонений, — затраты Sm соответственно.
Организация контроля безопасности проведения конкретного процесса в рассматриваемых условиях может состоять в определении значений некоторой величины xk, указывающих на необходимость (≠ 0) и кратность (xk = 1,2,3, …) осуществления контроля за каждой отдельной операцией, а задача его совершенствования – в выборе оптимального (в определенном смысле) вектора X = {x1, x2, …, xk, …, xm}. В качестве критерия оптимальности и ограничений должна использоваться организационная характеристика E{ψ} = E(t) или её компоненты: ресурсы, имеющиеся у исследуемой и обеспечивающей её безопасность человеко-машинных систем – τ или S.
Для уточнения содержания вектора E{ψ}, необходимо учитывать, что цель обеспечения безопасности заключается в удержании в допустимых пределах или минимизации суммарных издержек, либо их одной компоненты – ущерба от происшествий и профессиональных заболеваний. Следовательно, при совершенствовании организации ее контроля, необходимо извлечь из данного вектора прежде всего вероятность отсутствия происшествий или предпосылок к ним – Pδ (τ) = 1-Q (τ) и математические ожидания величин ущерба – Mτ[Y] или затрат – Mτ [S] с ними связанных.
С учетом изложенного, обоснование рекомендаций по совершенствованию контроля безопасности проведения производственных процессов может быть сведено к постановке и решению ряда оптимизационных задач, отличающихся либо оптимизируемыми параметрами, либо целевой функцией и ограничением.
Цель совершенствования безопасности проводимых работ состоит в выборе кратности контроля, т.е. в выделении операций, подлежащих двойному, тройному и т.д. контролю, с последующим устранением выявленных нарушений.
Математически это сводится к нахождению вектора X = {x1, x2, …, xk, …, xm}, реализующего одно из таких двух условий.
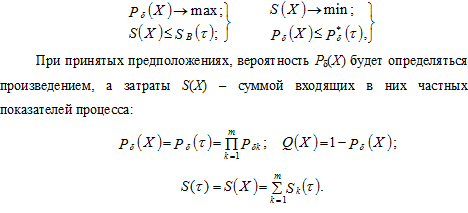
где Pδk(τ) – вероятность выполнения k-ых технологических операций без происшествий и предпосылок к ним в течение времени τ,
Sk (τ) = Skk(τ) + Sky(τ) – затраты, необходимые для организации в это же время контроля безопасности проводимых работ и устранения выявленных отклонений.
При условии пренебрежения ошибками первого рода при контроле (k01 = 0),
а соответствующие этим организационным процедурам и допущениям затраты определяются такими соотношениями:
Sk (τ) = xk [Skx + bkSyx];
Sk (τ) = Sk1 + (τ) k100 Sy1 + Sk2 + (τ) k110 k200 Sy2 + …+
+ Skx‘ + Q‘k (τ) k110k210…kx-110 kx00 Syx΄,
где bk = [1 – Qk(τ)] k11 + Qk (τ) k10 – параметр качества системы контроля;
Pki = μn – условные вероятности устранения выявленных внештатных ситуаций на i—ом его шаге (n-ом шаге обучения специалиста);
Skx΄, Syx΄ – затраты на организацию контроля и устранения возникающих на его i-ом шаге предпосылок к происшествиям. Следующим шагом оптимизации контроля является определение численности работающих в контролирующих органах.
Ограничения будут определяться исходя из предполагаемой эффективности контроля и устранения возможных отклонений, сравнения ее с эффективностью технических и технологических средств защиты. Значение P*δ (τ) может задаваться также на основе статистических соотношений между числом происшествий и предпосылок к ним, обычно составляющих 1 : 300 – для аварий и поломок или 1 : 500 – для несчастных случаев с работающими [156].
В качестве одного из возможных методов решения предложенных задач оптимизации целесообразно использовать градиентный метод отыскания экстремума. При этом оказывается, что градиентом на j—ом шаге движения по координате хk удобно использовать следующее отношение:
Уyk = ∆Pδ(xjk ϵ X) / ∆S(xjk ϵ X).
Рекомендуются такие начальные точки поиска экстремума – {xok} и соответствующие им решения: Pδ(Xo) – для прямой постановки или S(Xo) – для обратной. Они должны определяться из выражений (3.126) ¸ (3.129), при условии подстановки в них таких значений параметров k00, k01, k10, k11, Pki, Ski, Syi, которые удовлетворяют решаемой задаче.
Для решения рассмотренных задач могут быть применены известные алгоритмы и соответствующие им программы [3]. Идея поиска экстремума обычно состоит в использовании операционных процедур, включающих операционное наращивание контроля до получения первого приемлемого решения, а затем последовательное улучшение полученного результата, за счет перераспределения средств, выделенных на контроль и коррекцию выполняемых операций.
Литература
- Мельникова Д.А, Яговкин Г.Н. Теоретические аспекты формирования систем управления профессиональным риском на опасных производственных объектах: монография /– Самара, ООО «Медиа – книга» 2014 – 120с.
- Gillet B. Introduction to operational research: a computer algorithmic approach. – Mc Grow hill inc. – 1976. – 386 p.
- Ротштейн А.П., Кузнецов П.Д. Проектирование бездефектных человеко-машинных технологий – К.: Техника 1992- 180с.[schema type=»book» name=»ОЦЕНКА ЭФФЕКТИВНОСТИ СИСТЕМЫ КОНТРОЛЯ ЗА СОСТОЯНИЕМ БЕЗОПАСНОСТИ НА ПРОМЫШЛЕННОМ ПРЕДПРИЯТИИ» description=»Разработана методика обоснования рациональной численности органов контроля за состоянием безопасности производственной деятельности, позволяющая производить поддержку принятия решений по оптимизации организационной структуры как системы в целом, так и ее элементов.» author=»Мельникова Дарья Александровна, Кривова Маргарита Андреевна, Яговкин Герман Николаевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-14″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.05.2015_05(14)» ebook=»yes» ]

