В статье дано задание SH -распределения в проективном пространсве Pn[6]. Построены нормализации в смысле Нордена[4] и квазинормали[3],[6] базисного подрасслоения SH -распределения в дифференциальной окрестности 1-го , 2-го и 3-го порядка. Изучение SH — распределений актуально, так как эти образы являются обобщениями специальных классов регулярных гиперполос[1] и гиперповерхностей, а также гиперполосных распределений[7]. Работа выполнена методом Лаптева Г.Ф.[2]. Индексы принимают значения:

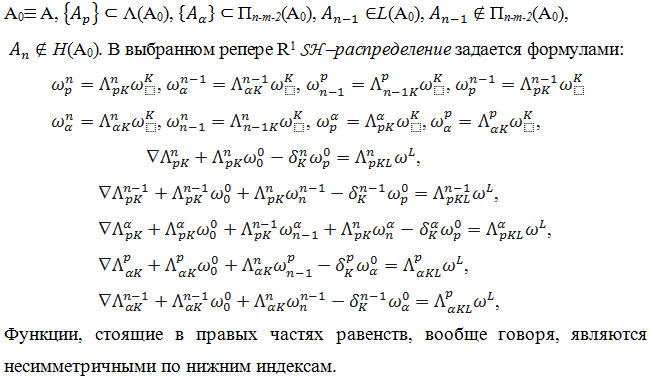
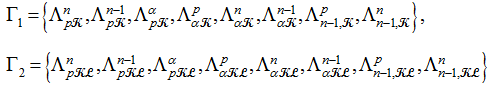
— фундаментальные геометрические объекты 1 –го и 2 –го порядка
SH –распределения. Имеет место теорема существования SH-распределения:
Теорема 1. В n –мерном проективном пространстве гиперплоскостное скомпонованное SH–распределение существует с произволом функций n аргумента.
- 2. Нормализации базисного Λ — подрасслоения
Определение. Будем говорить что базисное Λ – подрасслоение данного SH–распределения нормализовано[4], если в каждом центре инвариантно присоединены нормали первого и второго рода в смысле Нордена плоскости Λ(А0), а именно:
1) нормаль 1-го рода –(n-m)-мерная плоскость, не имеющая с плоскостью Λ(А0) других общих точек, кроме ;
2) нормаль 2-го рода (А0)- (m-1)-мерная плоскость, не проходящая через точку А0 и лежащая в текущей плоскости базисного –распределения.
- I. Кроме того, будем полагать, что нормаль 1-го рода содержит оснащающую плоскость :
где
Требование инвариантности нормали , накладывает следующие условия на величины {}:








Список литературы:
- Вагнер В.В. Теория поля локальных гиперполос. Тр. Семинара по векторному и тензорному анализу — 1950. — Вып.8. — С. 197-272.
- Лаптев Г.Ф. Дифференциальная геометрия погруженных многообразий. Теоретико-групповой метод дифференциально-геометрических исследований. Тр. Моск. мат. об-ва. — 1953. — Т.2. — С. 275-382.
- Лаптев Г.Ф., Остиану Н.М. Распределения m-мерных линейных элементов в пространстве проективной связности. Тр. Геометрического семинара. ВИНИТИ. 1971, Т3, с.49-94.
- Норден А.П. Пространства аффинной связности.-М.: Наука, 1976.
- Остиану Н.М. Распределение гиперплоскостных элементов в проективном пространстве. Тр. Геометрического семинара. ВИНИТИ. 1973,Т4,с.7-70.
- Попов Ю.И. Основы теории трехсоставных распределений проективного пространства. Монография. Санкт-Петербург. Из-во С-Петербургского университета, 1992.-172с.
- Cтоляров А.В. Проективно-дифференциальная геометрия регулярного гиперполосного распределения m-мерных линейных элементов. — В кн.: Проблемы геометрии (Итоги науки и техн. ВИНИТИ АН СССР), М., 1975, Т. 7, с.117-151.
- Столяров А.В. Двойственная теория оснащенных многообразий. Монография. Чебоксары. 1992.-290с.[schema type=»book» name=»SH -РАСПРЕДЕЛЕНИЕ ПРОЕКТИВНОГО ПРОСТРАНСТВА» author=»Будылкин Андрей Александрович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-05-24″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.01.2015_01(10)» ebook=»yes» ]

