- Introduction.
Research in area of electromagnetic metamaterials has been drastically increased in the last 20 years: in 1990th the amount of papers in this area was counted in ones, nowadays thousands of papers are published annually [4, p. 8]. The main reason for this rise of interest in this field is due to demands of technologies, which require materials with unique properties, but also discoveries in new materials can result in development of new technologies. Examples of such technologies would be: devices for control of radiation in THz frequency spectra, reflectionless coatings, Stealth-technologies and many others [6, p. 448]. Developments of described technologies require the thorough research of electromagnetic waves behavior in metamaterials.
To describe gradient transmission line, which can be viewed as a heterogeneous section (with spatial dependency of parameters), situated between two homogeneous sections (no spatial dependency of parameters), two independent functions must be taken into account [3, p. 53]: spatial distribution of capacity C(z) and inductance M(z). The spatial-temporal variations of current I and voltage V are known to be characterized by the telegraph equations, describing the propagation of electromagnetic wave in z-direction [5, p. 251]:

The second equation in (1) is reduced to identity, while the function is governed by the first equation, which reads in this case as:
![]() (4)
(4)
This paper will overview aspects of propagation characteristics of electromagnetic waves in gradient transmission lines based on recently developed mathematical model [1, p. 15]. The exact analytical solution of equation (4) is presented in the Chapter 2. This solution illustrates the formation of heterogeneity–induced plasma-like dispersion in the gradient transition section of transmission line, resulting in the appearance of some characteristic frequency , ensuring the formation of spectral ranges with both real and imaginary wave numbers. In Chapter 3 reflectance and transmittance spectra of two gradient transmission lines with different physical properties will be considered and graphically visualized. General idea of practical usage of gradient transmission lines in areas of process safety will be shown and the results of paper will be summarized in Conclusion (Chapter 4).
- Heterogeneity – induced dispersion of gradient medium
For better understanding of electromagnetic waves characteristics in gradient transmission line, definition of heterogeneity-induced dispersion must be introduced and this dispersion must be mathematically described. Smooth spatial distribution of capacitance and inductance of nanofilms, which thickness is comparable with the length of electromagnetic wave induce strong non-local dispersion that drastically changes the propagation of electromagnetic waves. This dispersion recently was described by means of mathematical model [2].






To analyze propagation of electromagnetic waves in gradient transmission line, two coefficients must be introduced: reflectance coefficient with respect to power |Rm|2 and transmittance coefficient given by the obvious relation:

The complex reflection coefficient for the problem discussed can be presented in the form (14); however, it’s real and imaginary parts are distinguished from those ones given in (16):

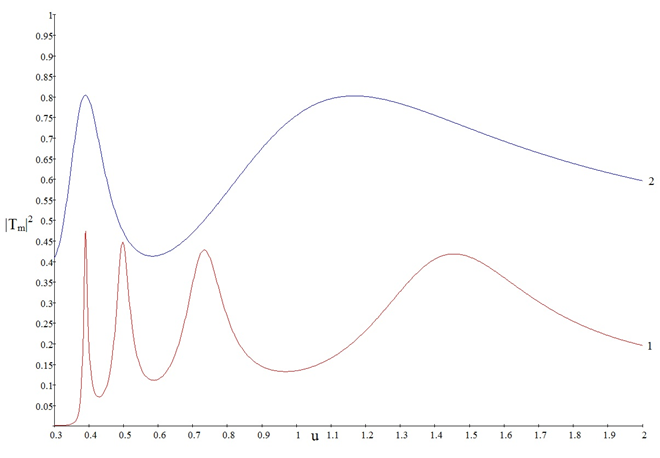
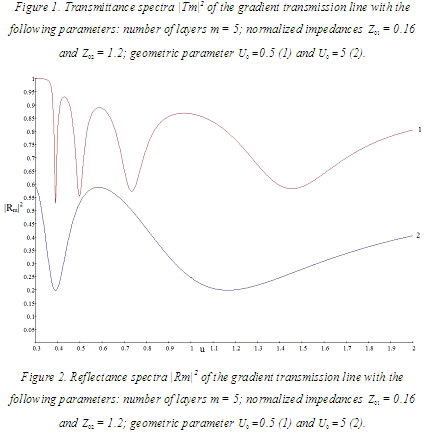
The graphs of reflectance and transmittance spectra have shown dependence of those spectra not only on frequency of the propagating wave, but also on geometric properties of the line, which opens up a possibility to design and optimize systems based on gradient transmission lines.
- Conclusion
The advances in nanotechnology provide opportunity to create devices with previously unattainable properties, so interest in this research field is evident. Gradient metamaterials is one of the applications of nanotechnology and in perspective can be used for various next-gen technologies, like extraordinary high-sensitive optical sensors, Stealth-technologies, gradient transmission lines with unique frequency properties and others.
By virtue of mathematical models constructed on the basis of exact solutions of Maxwell’s equations, it is possible to analyze in detail the behavior of electromagnetic waves propagating along the gradient transmission lines. The results show that the processes of transmission and reflection of waves are complex and depend not only on the frequency, but also on the geometric properties of the line.
References
- A.B. Shvartsburg, A.A. Maradudin, Waves in Gradient Metamaterials, WSPC, 2013. – 15 p.
- A.B. Shvartsburg, N.V. Silin, Propagation of Microwaves in Gradient Transmission Lines: Exactly Solvable model, Physica Scripta, 2015.
- A.B. Shvartsburg, Tunneling of electromagnetic waves – paradoxes and perspectives, Physics – Uspekhi, 2007. – 53 p.
- O.D. Volpian, A.I. Kuzmichev, Negative wave refraction, Avers, 2012. – 8 p.
- R. Collins, Field Theory for Guided Waves, Wiley 1991. – 251 p.
- Yu. V. Gulyaev, A. N. Lagar’kov, S. A. Nikitov, Metamaterials: fundamental research and using perspectives, Vestnik Rossiiskoi Akademii Nauk, 2008. – 448 p.[schema type=»book» name=»PROPAGATION CHARACTERISTICS OF ELECTROMAGNETIC WAVES IN GRADIENT TRANSMISSION LINE» description=»Propagation characteristics of transmission lines with smooth continuous spatial distribution of capacitance and inductance (gradient transmission line) is considered in the framework of recently developed mathematical model. Strong heterogeneity-induced artificial dispersion is described by means of this model. Reflectance and transmittance spectra are shown on example of different gradient transmission lines. In conclusion, applicability of gradient transmission lines in areas of process safety and technical condition control are described.» author=»Nesterov Iurii Gavriilovitch, Silin Nikolay Vitalievich» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-01″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_26.09.15_10(18)» ebook=»yes» ]

