В работах [1-5] был предложен так называемый информодинамический метод характеризации сложных структур. В качестве таковых, например, можно указать мезомасштабные системы естественных неоднородностей, идентифицируемые в кварцевых, металлических стеклах и аморфных пленках. Появление подобных систем дефектов является следствием существенной неравновесности условий появления таких объектов. Информодинамический метод отталкивается от построения координационных древесных графов Кэли (ДГК) для решеточных или сеточных систем вышеуказанных планарных сред [1, 3, 6].
В общем случае ДГК обладают случайной ветвистостью кустов на уровнях древесной иерархии, что позволяет ввести соответствующие вероятностные меры. Если рассматривать приближение входящих ветвей, то наблюдается внутриуровневая межкустовая локальная пересекаемость. Это, в свою очередь, обеспечивает наличие непрерывных «звездчатых» фронтов, которые дают возможность построить коаксиально вложенную систему скорлуп Мандельброта.
На квазистохастических ДГК можно ввести перколяционные термины и рассматривать преобразования в направлениях «центр↔периферия». По своей природе координационные ДГК являются эстафетными деревьями. Это равносильно Марковской цепной логике в радиальном направлении. С точки зрения геометрической, ДГК наделяются ультраметрикой.
ДГК в целом, отображающие сетевые структуры, с позиции теории сложных систем [7, 8] можно считать симплициальными комплексами. Последнее означает, что сами решеточные, сеточные системы и ДГК, их отображающие, необходимо изучать методами декомпозиции, причем именно симплициального типа [7]. Понятие симплициальности подразумевает некоторое весьма общее свойство ДГК в смысле топологического подобия.
Симплициальность имеет довольно тесную аналогию с общим принципом скейлинга, адаптированного на координационные ДГК. Это обстоятельство, в свою очередь, повлечет конструктивную параллель фрактальных понятий.
В настоящей статье сосредоточимся на выяснении характера структурного упорядочения решеточных, сеточных систем. Обычно в статистических, теоретико-вероятностных методиках уделяют внимание идентификации эмпирических статистик – распределений неоднородностей, отдельностей по размерам. Функции распределений, например, зерен структуры строятся на уровне распределения зерен по площадям. Этот простой подход можно обобщить, используя спектральные меры и корреляционный подход [9]. Вышеизложенная методология делает центральным моментом выделенное подмножество отдельностей, неоднородностей, статистика которых обычно восстанавливается из эмпирических распределений, пользуясь известным методом проверки статистических гипотез. Предлагаемое в работе древесно-графовое представление сеточных структур базируется на так называемом [q-, p-] алфавите, где q-компонента ответственна за типы плиток, ячеек и т.д., а p- указывает на тип непосредственной координации. В древесных графах Кэли на первый план выходит реберная p-компонента, а именно, координация. Именно структура координаций ДГК наполняет содержанием перколяционную задачу в неклассическом понимании.
Реализовать дальнейшее продвижение в этом направлении можно, используя теорию перечисления графов [10]. Построив на ДГК соответствующие перечисляющие структуры, в частности, вероятностные перечисляющие полиномы (ВПП), на них можно задать соответствующие энтропийные, дивергентные функционалы. И далее рассматривать протекание уже энтропийных функционалов на ДГК, через которые идентифицируется тип, характер дальнего порядка в решеточных, сеточных системах.
Кроме рассмотрения задачи перколяции энтропии, можно ввести двухточечные меры, например, информационную дивергенцию Бонгарда [11], структура которой более сложна, чем дивергенции Кульбака [12]. Как для всякой информационной меры, необходимо задание двух систем отсчета. Тогда дивергенция Бонгарда, фактически, становится информационным расстоянием, а метрические свойства следует при этом проверять специально. В случае Вайдовских оценок дивергенция Бонгарда запишется следующим образом:
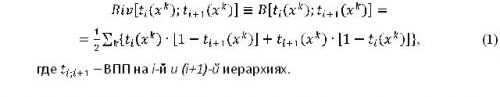
По своей логике дивергенция Бонгарда является средневзвешенной мультипликативной комбинацией вероятностей i-го уровня на дополнение (i±1)-го уровня. Перколяция информодинамических функционалов будет также иметь прямое отношение к диагностике дальнего порядка-беспорядка решеточных, сеточных систем и их древесных графов. Тем самым, рассматриваемый метод диагностики структуры сложных решеточных систем и паркетов будет базироваться на энтропийных, дивергентных функционалах.
Применим информодинамический метод к квартетной кристаллографической решетке (рис.1а), которая удовлетворяет трансляциям Браве.

Рисунок 1. Квартетная решетка (а) и ее ДГК (б) в алфавите [1q x 2p]
На рис.1б показан древесный координационный граф Кэли квартетной решетки в алфавите [1q x 2p], он наследует симметрию квартетной решетки. ДГК исследуется при помощи симплициальной декомпозиции, которая в данном случае реализуется в кустовом представлении. Для получения верхних оценок типы вершин и связей не различаются. Симплициальная декомпозиция позволяет привлечь теорию перечисления графов, которая приводит к аналитической форме записи ПП, ВПП. Данные структуры, а также энтропия Вайда и дивергенция Бонгарда в аналитическом виде приведены в табл.1.
Таблица 1.
Аналитические выражения для перечисляющих структур и информодинамических функционалов на ДГК квартетной решетки

Из рассмотрения табл.1 видно, как отражается квартетная симметрия решетки в поведении коэффициентов ПП. Переходя к ВПП, замечаем, что в прямом потоке исчезают кусты пятой степени ветвистости, а в обратном – первой и второй. Инвариантными остаются только кусты с троичной ветвистостью. Тем самым, квартетное ДГК близко к тетрадному дереву Бёте (рис.2), только в последнем отсутствует межкустовая локальная пересекаемость.
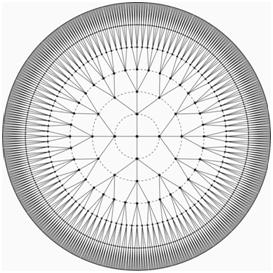
Рисунок 2. Тетрадное дерево Бёте (коэффициент ветвления k=3)
Из табл.1 также видно, что энтропийный функционал и мера Бонгарда в асимптотике стремятся к нулю. Для них была решена задача проверки гипотез по отношению к усеченному распределению Парето.
В целом перколяционные энтропийные зависимости на ДК квартетной решетки относятся к гиперболическому классу с критическими индексами ; . Аналогичными характеристиками обладает и мера Бонгарда с критическими индексами ; . Совпадение этих критических индексов указывает на высокое согласование квартетной решетки в перколяционном транспорте, который описывается как в терминах энтропии состояний, так и через двухточечные информационные меры типа дивергенции Бонгарда. По супремальной оценке такой тип дальнодействия квартетной кристаллографической решетки можно назвать «гравитационным» или «кулоновским».
Далее применим информодинамический метод к бигексагональной мозаике Дюно-Каца. Это одна из простейших квазикристаллических структур [13, 14], которая минимально «отстоит» от классических решеток. Данная мозаика показана на рис.3а.
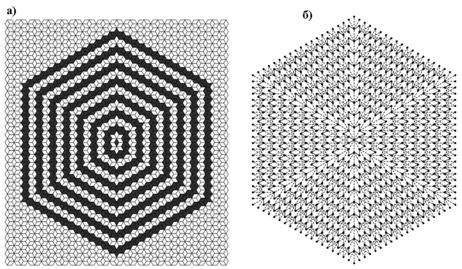
Рисунок 3. Бигексагональная мозаика Дюно-Каца (а) и ее ДГК (б)
Она сформирована фронтальным морфогенезом от двух минимально пересекающихся гексазвезд. В основе бигексагональной мозаики лежит трехуровневый алфавит, составленный из гексаромба, гексазвезды, и двух гексазвезд, пересекающихся по гексаромбу.
Согласно общей методике отображения, был построен координационный древесный граф Кэли для этой мозаики, который показан на рис.3б. Из этого рисунка видно, что по направлениям симметрий идут кусты пятой степени ветвистости, а в секторах наблюдается квартетная симметрия кустов, причем всегда две крайних ветви обрываются, а срединная пара ветвей продолжает расти. Стоит заметить довольно сильную локальную внутриуровневую пересекаемость кустов.
Данный граф допускает симплициальную кустовую декомпозицию с алфавитом [1q x 2p] (рис.3б), хотя в дальнейшем связи по типу координации не различаются. Следующим шагом является применение теории перечисления графов. Для этого составляются ПП, ВПП, которые приведены в табл.2.
Таблица 2.
Аналитические выражения для перечисляющих структур и информодинамических функционалов на ДГК бигексагональной мозаики


Значение критических индексов указывает на весьма сильное дальнодействие этой квазикристаллической структуры. В данном случае можно говорить о сверхдальнодействии по отношении к «кулоновскому», «гравитационному» типу дальнодействия в квартетной решетке. Также стоит отметить, что обратный поток менее дальнодействующий. Из (2) также можно заключить, что критические индексы в обратном потоке являются совпадающими, и в этом мы видим результат воздействия «отражения» от бесконечного горизонта ДГК. Остальные неравенства (2) следует признать существенными. Выражения (2) в целом также можно считать своеобразным проявлением обобщенного II-го начала термодинамики для бигексагональной мозаики Дюно-Каца.
Пользуясь выражениями энтропии и дивергенции табл.2, были получены следующие значения соответствующих асимптотик:
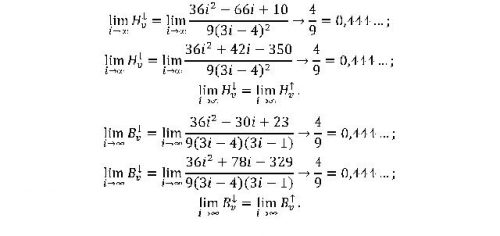
Последние выражения указывают, что возможно существование таких, в данном случае, квазикристаллических решеток бигексагонального типа, в которых существенно ненулевая асимптотика. Тогда, наряду с гиперболичностью энтропийной перколяционной зависимости с критическими индексами , в качестве нового признака вводится факт ненулевой остаточной энтропии. Сами значения энтропии и дивергенции не максимальны, это указывает на наличие значительного порядка. А их асимптотическое равенство может свидетельствовать о совершенстве системы.
ЗАКЛЮЧЕНИЕ
Предложен новый информодинамический метод диагностики дальнего упорядочения обобщенных решеточных систем. Этот метод основан на понятии координационного порядка. Для адекватного отображения координационных отношений предложен формализм ДГК, которые изучаются в эстафетном приближении. В качестве функционалов, идентифицирующих дальний порядок, используются энтропия и дивергенция Бонгарда в форме Вайда. Изучалась зависимость вышеуказанных функционалов как вариант задачи перколяции в нетрадиционной постановке на ДГК. Объектами приложения данного метода в настоящей работе являются квартетная решетка и бигексагональная мозаика, которые ранее не рассматривались в таком подходе. Для указанных систем удалось установить соответствующие типы дальнодействия.
Показано, что для квартетной решетки перколяционная зависимость энтропии относится к гиперболическому типу с критическим индексом, не превосходящим единицы. Это так называемый «гравитационный», «кулоновский» тип дальнодействия. Бигексагональную мозаику Дюно-Каца можно отнести к такому классу дальнодействия, где критический индекс значительно меньше единицы. Эта решетка и соответствующее ДГК имеют более сложную топологическую структуру со своими степенями дальнодействия, а в асимптотике существует остаточная энтропия, величина которой равна 4/9=0,444… Тем самым, диагностика дальнего упорядочения сводится к типу гиперболичности по критическому индексу и поведению энтропийных функционалов в асимптотиках.
Предлагаемый метод может быть универсальным количественным идентификатором различных систем с целью определения характера их дальнего упорядочения.
Работа выполнена при поддержке ДВФУ, проект № 14-08-03-37_и.
СПИСОК ЛИТЕРАТУРЫ
- Юдин В.В., Писаренко Т.А., Любченко Е.А., Савчук Е.А. Случайные координационные деревья Кэли для сеточных мезоструктур кварцевых и металлических стекол // Кристаллография. 1999. т.44, №3. с.413-421.
- Юдин В.В. и др. Мозаика Пенроуза как древесно-графовая стохастическая решетка // Кристаллография. 2002. т.47, №2. с.224-231.
- Юдин В.В., Писаренко Т.А., Любченко Е.А. Информодинамика сетевых структур. Вероятность. Древесные графы. Фракталы. Владивосток: Изд-во ДВГУ, 2003. 243 с.
- 4. Юдин В.В., Титов П.Л., Михалюк А.Н. Энтропийная мера характера порядка-беспорядка решеточных систем в представлении координационных древесных графов Кэли // Теоретическая и математическая физика, 2010, Т.164. С.88-107.
- A. Mihalyuk, P. Titov, V. Yudin. Physica A. 389, 4127 (2010).
- Юдин В.В., Писаренко Т.А., Любченко Е.А., Чуднова О.А. Обобщенные решеточные системы как сверхперколирующие структуры // Изв.РАН. Сер.Физ. 2001. №10. с.1405-1410.
- Касти Дж. Большие системы. Связность, сложность, катастрофы. М.: Мир, 1982. 216 с.
- Айзерман М.А. и др. Динамический подход к анализу структур, описываемых графами (Основы графодинамики) / Сб. науч. тр. «Исследования по теории структур» М.: Наука, 1988. с.5-76.
- Юдин В.В. Стохастическая магнитная структура пленок с микропоровой системой. М.: Наука, 1987. 236 с.
- Харари Ф., Палмер. Э. Перечисление графов. М.: Мир, 1977. 396 с.
- Бонгард М.М. Проблемы узнавания. М.: Наука, 1967. 318 с.
- Кульбак С. Теория информации и статистика. М.: Наука, 1967. 400 с.
- Гратиа Д. Квазикристаллы // УФН. 1988. т.156. вып.2. с.347-364.
- Стивенз П.В., Гоулдман А.И. Структура квазикристаллов // В мире науки. 1991. №6. с.19-28.[schema type=»book» name=»ОЦЕНКА УПОРЯДОЧЕНИЯ РЕШЕТОЧНЫХ СИСТЕМ В ДРЕВЕСНО-ГРАФОВОМ ПРЕДСТАВЛЕНИИ» author=»Титов Павел Леонидович, Щеголева Светлана Анатольевна, Овсянников Артур Сергеевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-06-13″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.12.2014_12(09)» ebook=»yes» ]

