Электронная теория твердого тела в настоящее время становится необходимой потребностью практики. Ее достижения в области создания новых полупроводниковых материалов, магнитных, сверхпроводящих, конструкционных и других соединений достаточно впечатляющи. Существенными характеристиками для решения данных задач являются такие свойства, как энергия основного состояния, энергия связи, распределение электронной плотности. Последняя характеристика дает наглядную картину межатомной связи, по которой можно судить об особенностях физических свойств.
При рассмотрении общей картины взаимодействия диэлектрического образца с переменным электрическим полем малой амплитуды, имеющим гармонический характер, используют систему линейных дифференциальных уравнений затухающих колебаний гармонического осциллятора:


Рисунок 1. Схема ионной трактовки электронной
конфигурации алмаза
На основании видоизмененной трактовки механизма реализации неполярной ковалентной связи, возникающей для каждой пары соседних атомов алмаза, предполагается, что одна их половина переходит в катионное состояние C4+, а другая – в анионное состояние C4– (рисунок 2) [1, с.33].
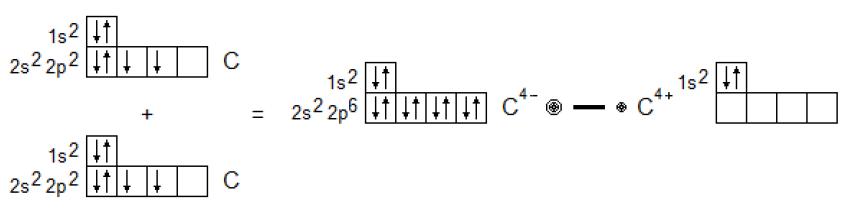
Рисунок 2. Схема видоизмененной трактовки образования
углеродной связи C–C
Таким образом, видоизмененная трактовка позволяет рассматривать частицы углерода в форме несжимаемых ионных шаров. При этом достаточно адекватная математическая модель их упругой электронной поляризации может быть описана с помощью соответствующей системы линейных дифференциальных уравнений, позволяющих перейти к комплексной диэлектрической проницаемости изучаемого образца [2-7].
Математическая модель, изображающая данный процесс, в виде:
|
(3) |
позволяет перейти к мнимой частотной характеристики комплексной электронной поляризуемости:
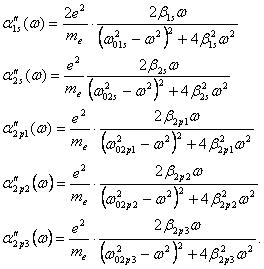 |
(4) |
На базе рассматриваемой математической модели был проведен вычислительный эксперимент, направленный на моделирование комплексной диэлектрической проницаемости кристалла, в рамках которого динамические параметры разбираемых процессов задавались абстрактными значениями вида:
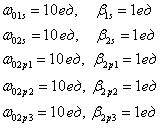
Результаты моделирования, проведенного на базе уравнений (2) и (4), представлены на рисунке 3.

Рисунок 3. Качественная МЧХ алмаза, соответствующая модели (3)

Рисунок 4. Электрон-вольтные спектры мнимой части
диэлектрической проницаемости алмаза [8]
Сравнивая данные физического эксперимента, представленные на рисунке 4 [8, с. 940], с результатами вычислительного эксперимента, можно отметить, что использование альтернативной трактовки электронной конфигурации алмаза позволяет получить графический образ резонансного режима наиболее адекватный реально наблюдаемым свойствам кристалла.
Таким образом, модифицированная модель наноструктуры алмаза позволяет наиболее точно изучить его оптические свойства в области установления процессов упругой электронной поляризации. Следовательно, ее практическое использование для изучения внутреннего строения кристаллических веществ может оказаться весьма полезным для дальнейшей эволюции теоретических основ физики конденсированного состояния, обеспечивающих развитие современных нанотехнологий.
Список литературы:
- Еремин И.Е., Остапенко А.А., Назаренко Н.В. Опосредованная визуализация наноструктуры алмаза. // Вестник ТОГУ. – 2013. — №4(31). – С. 31-42.
- Еремин И.Е., Жилиндина О.В. Моделирование упругой электронной поляризации композиционных электрокерамик. I // Информатика и системы управления. – – № 1(15). – С. 28-38.
- Еремин И.Е., Жилиндина О.В. Моделирование упругой электронной поляризации композиционных электрокерамик. II // Информатика и системы управления. – – № 3(17). – С. 27-33.
- Еремин И.Е., Жилиндина О.В. Моделирование упругой электронной поляризации композиционных электрокерамик. III // Информатика и системы управления. – – № 4(18). – С. 11-20.
- Еремин И.Е. Кибернетическая теория поляризации щелочно-галоидных кристаллов. I // Информатика и системы управления. – – № 1(19). – С. 40-45.
- Еремин И.Е. Кибернетическая теория поляризации щелочно-галоидных кристаллов. II // Информатика и системы управления. – – № 2(20). – С. 50-59.
- Еремин И.Е. Кибернетическая теория поляризации щелочно-галоидных кристаллов. III // Информатика и системы управления. – 2009. – № 3(21). – С. 20-26.
- Соболев В.В., Тимонов А.П., Соболев В.Вал. Тонкая структура диэлектрической проницаемости алмаза // Физика и техника полупроводников. – 2000. – Т. 34, № 8. – С. 940-946.[schema type=»book» name=»МАТЕМАТИЧЕСКАЯ МОДЕЛЬ НАНОСТРУКТУРЫ АЛМАЗА» description=»Углерод и его аллотропные модификации имеют большое практическое значение в жизни человека, а также в технологических процессах, как инструментальный и конструкционный материал. Эффективное математическое моделирование его диэлектрических свойств, является в настоящее время актуальной задачей. Данная работа посвящена построению математической модели электронной конфигурации ковалентной неполярной химической связи алмаза эквивалентно отражающей диэлектрические свойства кристалла в области упругой электронной поляризации и сравнению результатов компьютерного моделирования с реально наблюдаемыми свойствами рассматриваемого материала. » author=»Еремин Илья Евгеньевич, Подолько Евгения Александровна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-11″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.05.2015_05(14)» ebook=»yes» ]

