В современной технике широко используются конструкции, изготовленные из композиционных материалов. Поэтому возникает необходимость изучения напряженно-деформационного состояния элементов конструкций в нелинейной постановке задачи с учетом вязкоупругих свойств материала [2, с.280; 6, с.384].
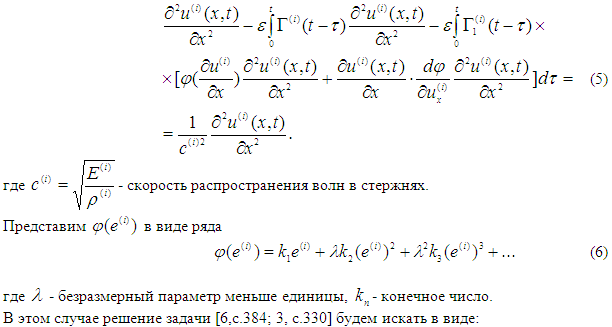
В этом случае решение задачи [6,с.384; 3, с.330] будем искать в виде:
Второе приближение находится из следующих систем уравнений
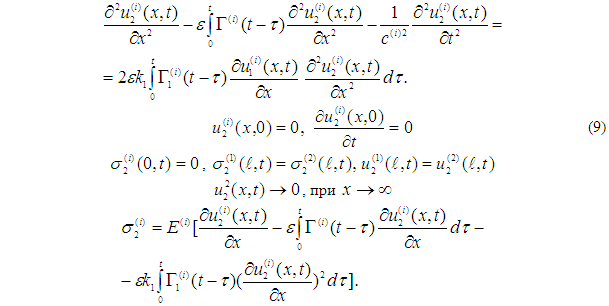
Для определения третьего приближения получаем следующую систему уравнений
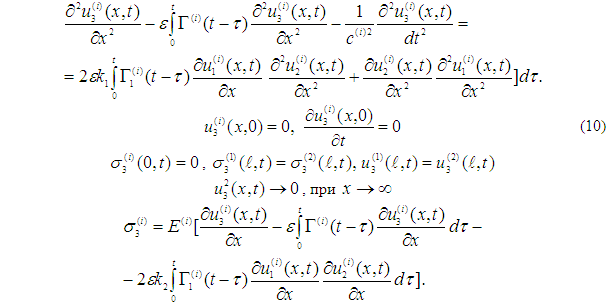
Аналогичным образом можем определить систему уравнений для нахождения последующих приближений.
Из систем уравнений (8) видно, что определение первого приближения решений является решением соответствующей линейной задачи вязкоупругости [4, с.53-57; 7].
Применяя интегральное преобразование Лапласа по времени к системе (8) получаем:
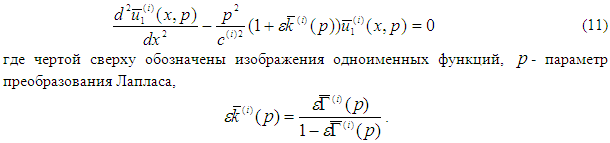
Решения этого уравнения в изображениях Лапласа для каждого стержня имеют вид:
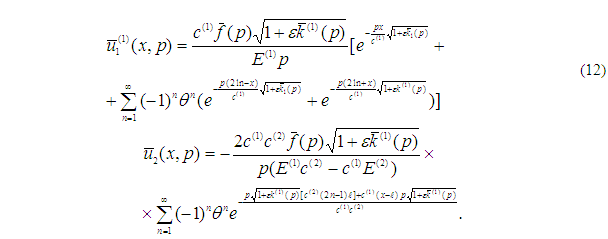
Отсюда видно, что вычисление оригинала первого приближения решений сводится к вычислению оригинала функций
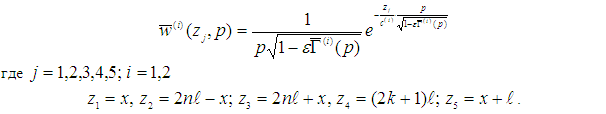
Оригиналы этих функций вычисляются по методике изложенной в работах [4, с.53-57; 7] и имеют вид:
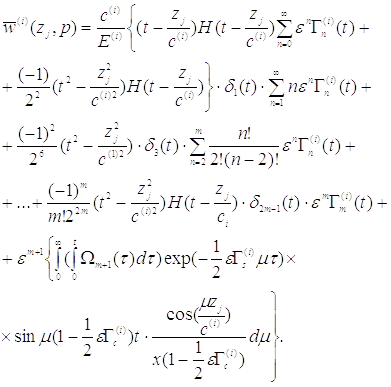(13)
— функция Хевисайда, — постоянная.
Тогда оригиналы первого приближения решений для каждого стержня определяются формулами
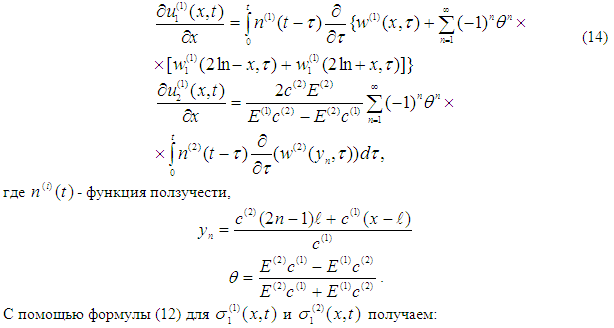
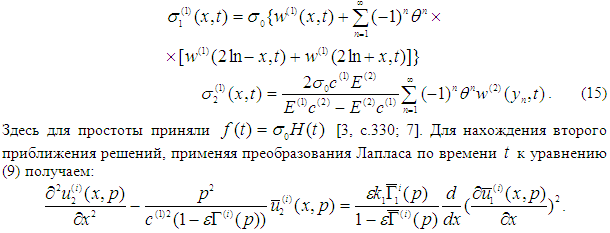
Общее решение этого уравнения для каждого стержня в изображениях Лапласа имеет вид:
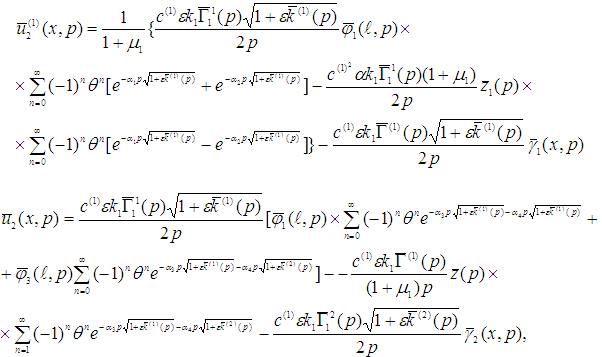
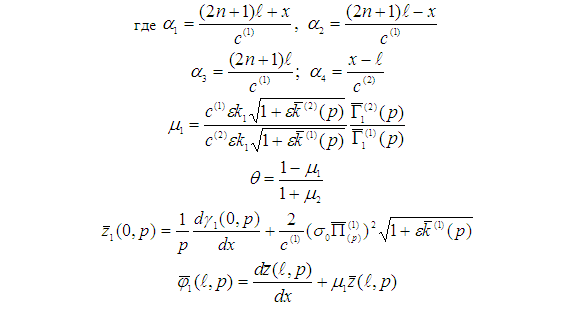
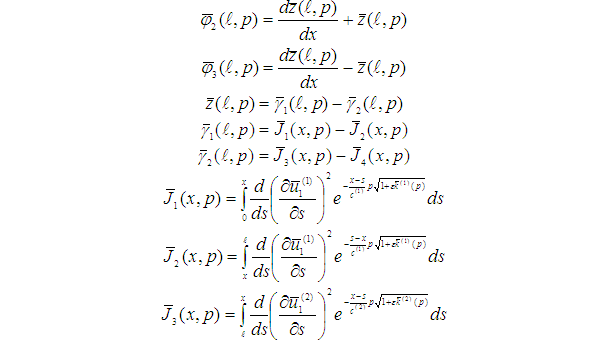
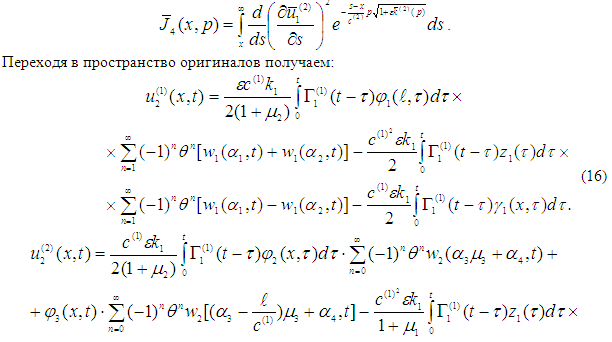
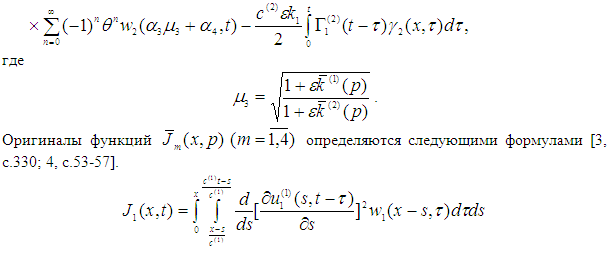
Аналогичным образом можем найти следующие приближения решений [4, с.53-57;1, с.70-72].
Здесь функция 
— характеризует линейную часть функции релаксации, а 
— является нелинейным ядром релаксации [6,с.384; 3, с.330].
Из формул (14) и (16) видно, что второе приближение зависит от нелинейного ядра . Это связано с решением, которое ищется в виде ряда (6) и решение убывает по экспоненциальному закону.
Литература
- Аршинов Г.А., Елисеев Н.И. Продольные волны в нелинейно вязкрупругом стержне. Изв.вузов, Северо-Кавказский регион, №3, 2003, с.70-72
- 2. Ильюшин А.А., Победря Б.Е. Основы математической теории термовязкоупругости. М. «Наука», 1970, 280 с.
- Ильясов М.Х. Нестационарные вязкоупругие волны. Баку «Азерб. Хава Йоллары», 2011, 330 с.
- Курбанов Н.Т. Исследование одномерных динамических задач линейной вязкоупругости. «Прикаспийский журнал», АГУ, Россия Астрахань, №2, 2008, с.53-57.
- Курбанов Н.Т., Алиева У.С. Исследование динамической устойчивости вязкоупругих стержней. «Динамикa i мiщнiсть мащин» Вiсник НТУ, Харьков Украина, 2012, с.86-91.
- 6. Работнов Ю.Н. Элементы наследственной механики твердых тел. М., «Наука», 1977, 384 с.
- Kurbanov N.T. and Nasibzada V.N. “Investigation of forced oscillations viscoelastik shells” International Journal of Current research, vol.7. Issue 07 18356 – 18360, India, 2015.[schema type=»book» name=»ИССЛЕДОВАНИЕ ОДНОМЕРНЫХ НЕЛИНЕЙНЫХ ДИНАМИЧЕСКИХ ЗАДАЧ ВЯЗКОУПРУГОСТИ» description=»В работе решается задача о распространении нестационарных динамических волн в стержневых вязкоупругих системах с учетом нелинейности среды, с помощью инте-грального преобразования Лапласа и методом последовательных приближений для произвольных наследственных функций. Показано, что все приближения зависят от нелинейного ядра наследственности, кроме первого приближения, а решение убывает по экспоненциальному закону.» author=»Курбанов Наби Тапдыг оглы, Алиева Ульвия Санган гызы, Рзаева Вафа Гюлага гызы» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-16″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.10.16_31(1)» ebook=»yes» ]