СРАВНИТЕЛЬНЫЙ АНАЛИЗ ТОЧНОСТИ МЕТОДОВ РЕШЕНИЯ ЗАДАЧИ ВНЕШНЕЙ БАЛЛИСТИКИ НЕУПРАВЛЯЕМЫХ РЕАКТИВНЫХ СНАРЯДОВ

Впервые реактивные снаряды (боевые ракеты) упоминаются очень давно. Есть основание полагать, что еще индусы и китайцы применяли боевые ракеты как зажигательные снаряды в глубокой древности. Об использовании боевых ракет китайцами имеются сведения у Марко Поло.

В России боевые ракеты были применены русской армией уже в турецкую кампанию 1828 года.

Одним из видов реактивных боеприпасов, стоящим на вооружении Военно-Морского Флота России, являются реактивные глубинные бомбы (РГБ) номенклатуры минно-торпедного вооружения.

Реактивные снаряды обладают рядом весьма ценных качеств (легкость и простота конструкции пусковых установок, большая маневренность, возможность быстрой концентрации мощного огневого залпа и др.). В то же время реактивные снаряды имеют весьма существенный недостаток – большое рассеивание.

Рассеивание реактивных снарядов в десятки, а иногда и в сотни раз превосходит рассеивание артиллерийских орудийных снарядов [7]. Поэтому основной проблемой для реактивных снарядов длительных сроков хранения является существенный недолет.

Этот недолет связан с длительными сроками хранения боеприпасов [2], в связи с геронтологическими изменениями порохового заряда (ПЗ) реактивного двигателя твердого топлива (РДТТ), так как изменяется средняя плотность пороха ввиду процессов массопереноса и автокатализа.

Решение прямой задачи внешней баллистики представляет возможность оценить эти изменения [3]. На сегодняшний день существует большое разнообразие способов решения этой задачи.

В этой связи возникает необходимость проведения сравнительного анализа точности различных методов решения основной задачи внешней баллистики (ОЗВБ).

Рассмотрим методы решения ОЗВБ с точки зрения анализа, обеспечиваемой ими точности. Для этого воспользуемся следующими методами решения основной задачи внешней баллистики [4]:

метод численного интегрирования (метод академика Крылова А.Н.);

метод интегрирования по относительному расходу топлива (метод профессора Шапиро Я.М.);

метод динамики средних с использованием среднего значения массы ракеты (метод профессора Денисова И.Г.);

метод табличного интегрирования.

При определении точности каждого из перечисленных методов решена ОЗВБ известных условий практических стрельб для нормального кондиционного боеприпаса [4].

Результаты решения задачи внешней баллистики для активного участка траектории реактивного снаряда полученными перечисленными методами [5] представлены в таблице 1.

Таблица 1

Основные характеристики активного участка траектории РГБ

Методы решения	Основные характеристики активного участка траектории РГБ
Методы решения	V_a, м/с	θ_a, град	X_a, м	Y_a, м
Метод численного интегрирования	268,7	40,2	69,7	65,0
Метод табличного интегрирования	268,3	39,8	70,0	64,5
Метод Шапиро Я.М.	265,3	39,8	72,8	59,5
Метод Денисова И.Г.	265,4	36,3	75,8	58,6

Эти результаты послужили основанием для проведения анализа точности, получаемых при их применении результатов.

Опираясь на полученные основные характеристики активного участка траектории, которые являются исходными данными для пассивной составляющей траектории, составим таблицу основных характеристик внешней баллистики РГБ (таблица 2).

Таблица 2

Основные характеристики внешней баллистики РГБ

Методы решения	Основные характеристики траектории в точке приводнения РГБ
Методы решения	X, м	ΔX, м	ΔX_отн, %	Y_max, м	V_c, м/с	T, с	θ_с, град
Метод численного интегрирования	5825	175	2,9	1400	213	34,1	-47,0
Метод табличного интегрирования	5544	456	7,6	1360	201	33,7	-49,4
Метод Шапиро Я.М.	5689	311	5,18	1345	208	33,4	-45,8
Метод Денисова И.Г.	5589	411	6,85	1166	208	31,1	-42,1

Протяженность пассивного участка траектории определим с помощью выражения:

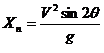, (1)

где Х_п — протяженность пассивного участка траектории РГБ;

V — скорость в конце активного участка;

θ — угол вертикального наведения реактивной бомбометной установки;

g- ускорение свободного падения.

Учитывая то, что выражение (1) справедливо для полета снаряда без учета сопротивления воздуха вводим поправочный коэффициент на сопротивление воздуха горизонтальной составляющей пассивного участка (K_x):

Такая процедура проводится для всех углов стрельбы. Проведя необходимые вычисления, составим таблицу, в которой представлен коэффициент сопротивления воздуха на пассивном участке траектории для определенных углов вертикального наведения и дистанции стрельбы РГБ (таблица 3).

Таблица 3

Коэффициент сопротивления воздуха пассивного участка траектории РГБ

Угол вертикального наведения, град.	Дистанция стрельбы, м.	Длина активного участка траектории, м.	Продолжительность пассивного участка траектории, м.	Поправочный коэффициент сопротивления воздуха на пассивном участке траектории.
13,5	550	162,2	1907	0,28
18,09	750	114,4	2653	0,28
23,12	950	105,3	3035	0,3
28,48	1100	100,4	3522	0,28
34	1200	91,6	3896	0,28
42	1300	78,8	4178	0,29

Анализ результатов вычисления поправочного коэффициента на сопротивление воздуха пассивного участка траектории показал, что в соответствии с принятыми допущениями о постоянной скорости снаряда, а следовательно и сопротивления воздуха, величина этого коэффициента 0,28.

Анализ результатов решения основной задачи внешней баллистики РГБ [5], выполненных перечисленными методами показывает следующее: наименьшую погрешность по горизонтальной дальности получаем при вычислении методом численного интегрирования ΔX_отн = 2,9%; максимальная погрешность получается при использовании метода табличного интегрирования, которая сопоставима с методом профессора Денисова И.Г. и составляет 7,6% и 6,85% соответственно. Промежуточную погрешность в 5,18% дает метод профессора Шапиро Я.М.

Как показано в [6] фактический максимальный относительный недолет составляет приблизительно 5% дистанции стрельбы. В этой связи можно сделать вывод о том, что для решения задачи внешней баллистики, с учетом геронтологических изменений ПЗ РДТТ применимы методы численного интегрирования и профессора Шапиро Я.М.

СПИСОК ЛИТЕРАТУРЫ

Анипко О.Б., Больших А.А. Экспериментальное исследование дальности стрельбы реактивными глубинными бомбами длительных сроков хранения. – Сб. науч. тр. АВМС имени П.С. Нахимова, г. Севастополь, 2012 – вып. 4(12). – С. 26-29.
Веннен Л., Бюрло Э., Лекорше А. Пороха и взрывчатые вещества. Пер. с фран. – М.: ОНТИ, 1936. – 652 с.
Окунев Б.Н. Основная задача баллистики и аналитические методы ее решения. – Л.: Технико-теоретическое издательство, 1934. – 524 с.
Новиков А.В., Касаточкин В.А., Фролов М.В. Методики расчетов траектории реактивных глубинных бомб. – Санкт-Петербургский военно-морской институт, 2001 г., 44 с.
Больших А.А. О точности некоторых методов решения задачи внешней баллистики неуправляемых реактивных снарядов длительного срока хранения. / науч. журн. — М.: ЕСУ, 2015. № 2(9). – С. 21 — 24.
Новиков В.В., Больших А.А. Корреция диапазона дальности стрельбы реактивными глубинными бомбами длительных сроков хранения. / Сб. тр. всероссийской науч.-практ. конф. «Корабельные и бортовые многоканальные информационно-управляющие системы» – СПб.: ОАО «ЦНИИ Гранит-Электрон», 2014.
Новиков В.В., Больших А.А. Особенности изменения баллистических и боевых характеристик реактивных глубинных бомб длительных сроков хранения. / Сб. науч. тр. межотраслевой науч. –практ. конф. «ВОКОР-2014» — Военное кораблестроение России: состояние, проблемы, перспективы. – СПб.: НИИ КиВ, 2014.[schema type=»book» name=»СРАВНИТЕЛЬНЫЙ АНАЛИЗ ТОЧНОСТИ МЕТОДОВ РЕШЕНИЯ ЗАДАЧИ ВНЕШНЕЙ БАЛЛИСТИКИ НЕУПРАВЛЯЕМЫХ РЕАКТИВНЫХ СНАРЯДОВ» author=»Больших Александр Александрович, Русин Вадим Витальевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-02″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_27.06.2015_06(15)» ebook=»yes» ]

euroasia

Похожие записи