Приоритетным направлением развития отечественного метрополитена в современных условиях является повышение надёжности эксплуатации подвижного состава. В рамках этого направления поставлена задача: безотказная работа и совершенствование конструкции вагона в соответствии с современными требованиями [2].
С целью увеличения межремонтного пробега вагонов метрополитена целесообразно провести исследование динамических свойств тележки.
Исследование динамических свойств конструкции можно проводить с использованием компьютерных программ, что позволяет оценить работоспособность системы, не прибегая к дорогостоящим испытаниям.
Однако достоверность результатов расчетов зависит от точности построения модели, — это подготовительный, но основной этап исследования.
Для решения динамических задач необходимо разработать модель исследуемой динамической системы и определить динамические нагрузки, взаимодействующие с динамической системой.
Разработка расчетной математической модели тележки состоит из следующих основных этапов:
- Построение геометрической трехмерной модели тележки с использованием рабочих чертежей. В качестве программного пакета для реализации применен SolidWorks;
- Создание расчетной математической конечно-элементной модели на базе геометрической.
- Разработка математической модели с использованием программного комплекса «Универсальный механизм» (UM) с применением методов моделирования динамики систем тел для анализа воздействия динамических нагрузок на конструкцию при движении по пути с разными скоростными режимами.
При разработке геометрической модели необходимо учитывать все особенности конструкции, которые могут влиять на жесткость рамы: форма сечений балок, толщины листов, внутренние диафрагмы, внешние ребра и накладки.
Построение расчетной конечно-элементной модели необходимо для решения задачи статики — определение напряженно-деформированного состояния рамы тележки от действия статических сил. Результат расчета покажет наиболее нагруженные области. На данном этапе главную роль играют особенности конструкции рамы и влияние масс подвесного оборудования.
Математическая расчетная модель рамы тележки ввиду большого количества дифференциальных уравнений создается с помощью компьютерной программы MSC.Patran. Все расчеты производятся методом конечных элементов. Благодаря заложенному расчетному методу математическая модель системы аппроксимируется конечными элементами, которые позволяют учесть сложную форму конструкции, ее упругие, инерционные и диссипативные характеристики.
В основе метода конечных элементов лежит дискретизация объекта с целью решения уравнений механики сплошной среды в предположении, что эти соотношения выполняются в пределах каждой из элементарных областей. Эти области называются конечными элементами. В пределах конечного элемента назначаются свойства ограничиваемого им участка объекта. Параметры назначаются в узлах элемента, а затем вводятся интерполирующие функции, посредством которых соответствующие значения можно вычислить в любой точке внутри элемента и на его границе. Задача математического описания элемента сводится к тому, чтобы связать действующие в узлах факторы. В механике сплошной среды это, как правило, перемещения и усилия [4, с.3].
Рассматриваемая геометрическая модель тележки вагона метрополитена состоит из рамы, которая опирается на буксы посредством витых цилиндрических пружин, и колесных пар (рисунок 1).
Рисунок 1. Геометрическая модель тележки вагона метрополитена
Также следует учитывать, что для создания расчетной модели, адекватной реальной конструкции, необходимо учитывать все конструктивные особенности соединения рамы с колесными парами.
На современном подвижном составе метрополитена для улучшения характеристик динамики движения помимо упругих элементов в первой ступени рессорного подвешивания в виде витых металлических пружин применяют резинометаллические шарниры для соединения рамы тележки с буксами.
Резинометаллические шарниры предназначены для реализации виброзащитного эффекта, — защита рамы и оборудования, закрепленного на раме, от динамических воздействий от пути.
В системе на собственных частотах происходят совместные колебания рамы с буксами и колесными парами. При введении упругих элементов появляются формы колебаний рамы тележки относительно букс и колесных пар. Причем, эти относительные колебания происходят на частотах во всем диапазоне эксплуатационных скоростей.
Учтенные же в геометрической модели пневморессоры при создании расчетной модели не рассматривались, поскольку они будут оказывать влияние на динамические характеристики, измеренные в надтележечном строении. В работе же поставлена задача исследования динамики непосредственно самой тележки.
При разработке расчетной модели в программе MSC.Patran на геометрическую модель наложена конечно-элементная сетка. Массово-инерционные характеристики модели соответствуют реальной конструкции. Жесткость пружин буксового рессорного подвешивания подобрана согласно паспортным данным.
На первом этапе исследования модели производился расчет нормальных форм колебаний методом конечных элементов (МКЭ), который показал, что собственные частоты рамы тележки лежат в области 30 — 80 Гц.
Расчет напряженно-деформированного состояния тележки при действии веса от максимальной загрузки вагона пассажирами [3, с.5] показал, что наиболее нагруженные области рамы в местах соединения поперечной балки с продольными. Это объясняется расположением пневморессор, передающих вертикальную нагрузку от кузова на раму тележки. Кроме того, расчет собственных частот и форм колебаний показал, что отмеченные области рамы тележки испытывают наибольшую деформацию.
На втором этапе выполнено исследование поведения тележки как динамической системы при вынужденных колебаниях. В качестве динамических возмущений для тележки вагона метрополитена приняты воздействия, передающиеся от рельсового пути на раму тележки.
Для расчета динамики конструкции применен модальный метод, основанный на вычислении частотных характеристик по собственным частотам нормальных форм колебаний.
Амплитудно-частотные характеристики (АЧХ) были вычислены:
а) на центральной балке,
б) на переходе продольной балки в концевую,
в) вблизи перехода центральной балки с концевой,
г) на вогнутых частях и на скосах концевых балок [4, с. 104].
На сравнительном расчете амплитудно-частотных характеристик можно оценить влияние резинометаллических шарниров при разработке адекватной расчетной модели тележки (рисунок 2).
Наибольший отклик на возмущение от пути в системе без резинометаллических элементов возникает на центральной балке, на рисунке 2,а (пунктирная линия) это характеризуется проявлением острых резонансных пиков на частотах 200 Гц, 210 Гц и 240 Гц. При введении упругих шарниров более динамически активными становятся концевая и продольная балка (сплошная линия – рисунок 2,б), что обусловлено формами колебания рамы относительно колесных пар при наличии резинометаллических элементов. При этом снижается амплитуда колебаний, однако значения резонансных частот смещаются в более низкую область эксплуатационных скоростей: 20 и 45 Гц, что соответствует скоростям движения 30 и 67,5 км/ч. На этих частотах проявляются изгибные колебания рамы тележки совместно с элементами, находящимися на ней [1. с.26]. Кроме того, колебания системы принимают периодический характер. Такие колебания могут стать резонансными при условии совпадения с колебаниями роторов тяговых электродвигателей в моторных тележках.
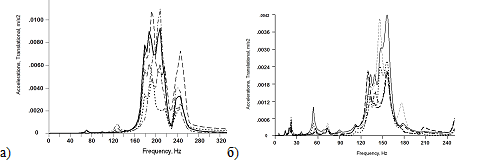
а — без учета резинометаллических шарниров; б — с резинометаллическими шарнирами
Рисунок 2. Амплитудно-частотные характеристики рамы тележки вагона метрополитена
Как показывает исследование, с применением резинометаллических шарниров достигается виброзащитный эффект, однако, из-за снижения общей жесткости конструкции значения собственных частот могут снизиться до эксплуатационных.
Методом отклика динамической системы тележки вагона метрополитена на стационарное случайное возмущение определены частоты, на которых наиболее вероятно возникновение резонансных колебаний.
Таким образом, предлагается подбирать параметры резинометаллических элементов индивидуально для каждой конструктивной схемы, исходя из результатов динамических расчетов.
Предлагаемая методика исследования динамических свойств тележки вагона предполагает обеспечение достоверности результатов на основании создания расчетной модели, адекватной реальной конструкции.
Список литературы:
- Бирюков И.В., Савоськин А.Н., Бурчак Г.П. Механическая часть тягового подвижного состава: учебник для вузов ж.-д. трансп. / И.В. Бирюков, А.Н. Савоськин, Г.П. Бурчак и др. Под ред. И.В. Бирюкова – М.: Транспорт, 1992. – 440с.
- Департамент транспорта и развития дорожно-транспортной инфраструктуры города Москвы [сайт] // 2014. 13 января URL: https://dt.mos.ru/presscenter/news_department/detail/923836.html (дата обращения: 24.01.2015).
- ТУ 3183-030-05804803-2002. Вагон метрополитена модели 81-740 Технические условия. СКБ Метро, 2002. 51с.
- Nastran. Basic Dynamic Analysis User’s Guide. — MSC.Software Corporation. U.S.A. 2004 — 546 с.[schema type=»book» name=»РАЗРАБОТКА МЕТОДИКИ ИССЛЕДОВАНИЯ ДИНАМИЧЕСКИХ СВОЙСТВ ТЕЛЕЖКИ ВАГОНА МЕТРОПОЛИТЕНА» author=»Вахромеев Алексей Викторович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-05-26″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.01.2015_01(10)» ebook=»yes» ]

