Введение небольшого количества ультрадисперсных добавок в материал матрицы позволяет улучшить механические и эксплуатационные свойства материалов. Известно, что высокий уровень физико-механических свойств алмазных порошков определяется большей величиной удельной поверхности и дисперсностью зерен, что, в частности, непосредственно вытекает из уравнения Холла-Петча, которое выполняется в широком (вплоть до 1 мкм) диапазоне размера зерен. Определяющим для функциональных свойств этих материалов является масштабный структурный фактор, поскольку он влияет на формирование структурно-чувствительных механических свойств – пределов прочности и текучести. Учитывая качественную корреляцию между пределом текучести и твердостью, можно прогнозировать повышение твердости, в том числе высокотвердых материалов. Высокая адсорбционная способность алмаза может оказывать положительное влияние на композиционный материал, получаемый методами порошковой металлургии совместным спеканием с металлом путем поглощения образующихся в процессе присутствующих в порошке металла газов. Кроме того, частицы ультрадисперсного и нанодиапазона характеризуются высокой поверхностной активностью, позволяющей осуществлять прочное сцепление с матрицей.
Цель работы — разработка и исследование свойств композиционного алмазосодержащего материала с улучшенными физико-механическими свойствами на основе металлической связки М2-01, с использованием природных порошков алмаза двух уровней дисперсности.
В работе использовалась стандартная связка оловянистой бронзы М2-01 (20% олова, 80% меди) с добавками 6 весовых % природных порошков алмаза (ППА) зернистости 315/250 мкм и 0,5-3 весовых % ультрадисперсного природного алмаза (УДПА).
Смеси из порошков приготовлялись с помощью смесителя типа «пьяная бочка», смешивание производилось в течение 2 часов с добавлением стальных шариков в количестве 1/3 от объема порошка. Компактирование порошковых смесей проводилось в стальных жёстких прессформах с помощью пресса ИП-500 при давлении 50 т. Спекание образцов осуществляли в вакууме 0,1∙10-3 Па в печи СНВЭ, при Т=700 0С в течении 1 часа. Полученные компакты показаны на рис. 1.

Рисунок. 1. Алмазосодержащие композиты на основе металлической матрицы М2-01
Твердость материалов измеряли на приборе FR-3e фирмы Leco согласно стандартной методике. Индентор – шарик диаметром 3,174 мм, нагрузка 588,4 Н (60 кг) по шкале HВ (поставили данные твердости по НВ).
Также проводились испытания на сжатие, по [1]. Испытания проводились на испытательной машине ИП-1250М с автоматизированным управлением. Для определения модуля упругости при сжатии использовалась зависимость деформаций от нагрузки деформаций от нагрузки. Согласно методу, описанному в [1], модуль упругости при сжатии определяется по следующей формуле:
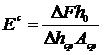 (1)
(1)
где, ΔF – ступень нагрузки, Н;
h0 – первоначальная высота, мм;
Δhср – средняя абсолютная деформация образца при нагружении ΔF, мм;
А0 – начальная площадь поперечного сечения цилиндрического образца.
Микроструктуру материала определяли с помощью оптического микроскопа при увеличении в 1000 раз. Снимки, полученные с помощью микроскопа, были обработаны с помощью программы Image Pro Plus 5.1.
Результаты измерения твердости приведены в таблице 1. Максимальная твердость достигается при введении в состав сплава микропорошка размерности -40 мкм.
Таблица 1
Зависимость значений твердости от зернистости и концентрации алмазных порошков
| Зернистость ПА, мкм |
Твердость, HВ |
||||||||
| Содерж.,% | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 3/2 | 41 | 42 | 43 | 44 | 43 | 45 | 47 | 47 | 46 |
| 7/5 | 41 | 43 | 47 | 44 | 43 | 44 | 43 | 42 | 42 |
| -40 | 41 | 44 | 48 | 48 | 51 | 51 | 51 | 50 | 50 |
| УДПА | 41 | 45 | 48 | 49 | 53 | 53 | 53 | 52 | 52 |
На рис. 2 показаны графики зависимости деформаций от нагрузок, полученные при испытании образцов на сжатие — для исходного образца и образца с добавлением 3% порошков природного алмаза.
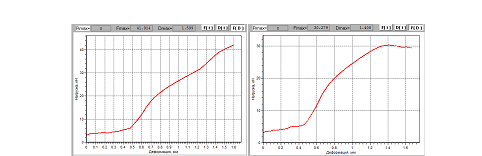
Рисунок 2. График зависимости деформаций от нагрузок для исходного образца и образца с добавлением 3%УДПА.
Для определения зависимости структуры сплавов от содержания добавок, были проведены металлографические исследования спеченных образцов.
На рис. 3 представлены снимки микроструктуры бронзовой матрицы без алмазного наполнителя и с разной концентрацией алмазных порошков. Матрица имеет типичное строение оловянистой бронзы, состоящей из двух фаз (α + δ). α-фаза представляет твердый раствор олова в меди, а δ-фаза — электронное соединение Cu21Sn8.

Рисунок 3. Снимки шлифованной поверхности исходного образца и образца с добавлением 2% частиц алмазных порошков при увеличении х1000
На микроструктурах бронзовой матрицы, в состав которых были введены алмазные порошки, на границах зерен и раздела фаз видны колонии точечных микрообъектов, образующие дисперсную систему агрегатного типа.
Точечные микрообъекты присутствуют и внутри зерен, образуя дисперсную субструктуру. Оптическая металлография не позволяет идентифицировать их морфологию — являются ли они мелкими алмазными частицами или нерастворенными микропорами.
Наличие на границах раздела микрочастиц алмаза повышает их развитость, увеличивая длину периметра микроструктурных объектов. Количественно степень развитости границ можно оценить средней плотностью границ, вычисляемой по формуле:
![]() (2)
(2)
где Pср – средний периметр по всем зернам;
Fср – средняя площадь по всем зернам.
С повышением концентрации алмазного наполнителя развитость границ раздела возрастает. Это наглядно демонстрируется зависимостью средней плотности границ как функции концентрации алмазного наполнителя (рис. 4а). Наличие максимума в районе 2 % концентрации указывает, что введение большего количества алмазного наполнителя нецелесообразно.
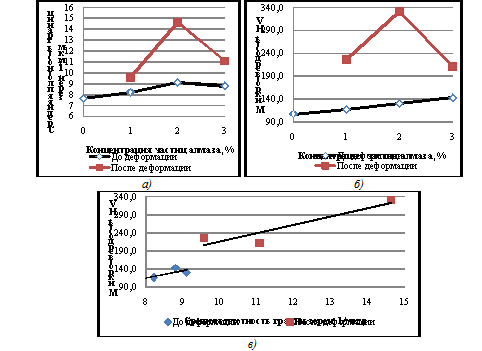
Рисунок 4. Влияние концентрации частиц алмаза на среднюю плотность границ зерен (а) и микротвердость (б) и зависимость микротвердости от средней плотности границ зерен (в) в образцах до и после деформации
Упрочнение поликристаллического материала связано с торможением дислокаций, при этом активным барьером для скольжения дислокаций являются дисперсные микрочастицы и границы раздела зерен и фаз. С повышением общей протяженности границ раздела повышается потенциальная способность блокировки дислокаций. Следовательно, с повышением степени развитости границ прочность материала должна возрастать.
Зависимость микротвердости матрицы от концентрации алмазного наполнителя (рис. 4б) отражает суммарное влияние дисперсионного и зернограничного механизма торможения дислокаций. Зависимость микротвердости от содержания алмазного наполнителя (рис.4б) и от средней плотности границ (рис.4в) убедительно подтверждают ранее высказанное предположение.
На рис.5 представлены оптические изображения микроструктур деформированных образцов после испытаний на сжатие.

Рисунок 5. Микроструктура образцов сплава М2-01 c 3% содержанием УДПА после деформации сжатия
Максимальное значение средней плотности границ зерен у деформированных образцов выше, чем у исходных. Этот факт объясняется увеличением количества микроструктурных объектов за счет более четкого выделения границ зерен или микротрещин на снимках. При деформировании дислокации, образующиеся в материале, будут концентрироваться на границах зерен и расширять последние, вследствие чего границы зерен у деформированных образцов при травлении будут четче проявляться.
Наблюдается корреляция расчетных значений средней плотности границ зерен у деформированных образцов по сравнению с исходными (рис. 4а). Это обусловлено теми же факторами, влияющими на среднюю плотность границ зерен.
Отмечена более высокая микротвердость деформированных образцов по сравнению с исходными. Это обусловлено механизмом дисперсионного упрочнения материала, при котором частицы алмаза, не осадившиеся на границах зерен и находящиеся внутри зерен работают при деформировании согласно механизму Орована при котором дислокации, возникающие при нагрузке, задерживаются вокруг частиц дисперсного наполнителя. Отмечается также корреляция значений микротвердости и средней плотности границ зерен в зависимости от концентрации алмазных порошков (рис. 4а и 4б). К тому же при деформировании поры, образовавшиеся в материале, ликвидируются. При этом в целом будет увеличиваться плотность материала.
Упрочнение за счет введения в материал матрицы порошков природного алмаза можно рассчитать согласно уравнению Орована:
![]() (3)
(3)
где λ –расстояние между ближайшими частицами;
G – модуль сдвига матрицы;
b – вектор Бюргерса;
ко– коэффициент, характеризующий тип взаимодействующих атомов с дислокацией
Среднее расстояние между частицами рассчитали по формуле:
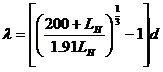 (4)
(4)
где LH – весовая доля наполнителя;
d – диаметр или толщина частиц наполнителя.
Значения прироста предела текучести за счет дисперсионного упрочнения, рассчитанные по уравнению Орована, приведены в таблице 2.
Таблица 2
Среднее расстояние между частицами (мкм) и дисперсионное упрочнение матрицы при введении ППА, МПа
|
Зернистость частиц |
7/5 |
3/2 |
-40 |
УДПА |
||||||||
| Содержание частиц, % | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| λ, мкм | 125.3
±1.25 |
98.19
±0.9 |
85.02
±0.8 |
52.19
±0.5 |
40.91
±0.4 |
35.42
±0.3 |
417.56
±4 |
327.30
±0.3 |
283.40
±3 |
6.26±
0.06 |
4.91±
0.05 |
4.25±
0.04 |
| ζN, МПа | 0.17
±0.01 |
0.69±
0.007 |
0.78±
0.008 |
1.22±
0.01 |
1.52±
0.01 |
1.74±
0.02 |
0.18±
0.002 |
0.23±
0.002 |
0.26±
0.003 |
8.24±
0.08 |
10.23±
0.1 |
11.63±
0.1 |
Согласно расчетам наибольшее упрочнение достигается при введении в матрицу УДПА, что в целом подтверждается экспериментальными данными. При изменении геометрии зерна за счет агломерации частиц наполнителей на границах раздела в материале уместнее всего рассчитать изменение свойств материала согласно теории зернограничного упрочнения.
С целью определения количественного увеличения прочности материала при добавлении частиц алмазных порошков за счет зернограничного упрочнения были проведены соответствующие расчеты по эмпирическому соотношению Холла-Петча:
(5)
![]()
где σ0 — некоторое напряжение трения, которое необходимо для скольжения дислокаций в монокристалле;
k — коэффициент Холла-Петча;
d – размер зерна.
Коэффициент Холла-Петча был взят применительно к меди и согласно [2, с. 85] является величиной переменной, зависит от такого параметра как средний размер зерна и варьируется в пределах 0,01-0,24 МПа*м1/2
Средний размер зерна был рассчитан согласно проведенным металлографическим исследованиям поверхности образцов:
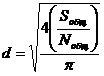 (7)
(7)
где Sобщ — общая площадь объектов;
Nобщ – количество объектов.
Расчеты показали, что по размер зерен у образцов с добавлением порошков природных алмазов меньше по сравнению с исходными. Этот факт можно объяснить тем, что частицы порошков алмаза оседая на границах зерен материала, меняют геометрическую форму и уменьшают среднюю площадь зерна.
Расчеты согласно соотношению Холла-Петча свидетельствуют об увеличении предела текучести материала при добавлении частиц порошков природного алмаза. Максимального расчетного значения предел текучести достигает при содержании наполнителей 1% (рис.6).
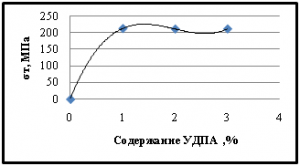
Рис. 6 Зависимость предела текучести от содержания УДПА
ВЫВОДЫ
Установлена взаимосвязь физико-механических свойств спеченного композиционного материала на основе оловянистой бронзы М2-01 с содержанием и зернистостью наполнителя в виде ультрадисперсного порошка природного алмаза.
Выявлено, что добавка мелкодисперсных алмазных частиц в количестве 1-3% в металлическую матрицу положительно влияет на качество получаемых композиционных материалов. В результате повышаются плотность, твердость, прочность и износостойкость, уменьшается пористость материалов, что позволяет прогнозировать улучшение эксплуатационных показателей работы изготовленного из них алмазного инструмента. Повышение прочностных характеристик композиционного материала происходит за счет механизмов дисперсного и зернограничного упрочнений, а также повышения плотности материала.
Список литературы:
- ГОСТ 25.503-97 «Расчеты и испытание на прочность. Методы механических испытаний на сжатие»
-
Козлов Э.В, Жданов А.Н., Конева Н.А. Барьерное торможение дислокаций. Проблема Холла-Петча // Физ. мезомех. – 2006. – С. 81-92.[schema type=»book» name=»РАЗРАБОТКА ИНСТРУМЕНТАЛЬНОГО МАТЕРИАЛА НА ОСНОВЕ МЕТАЛЛИЧЕСКОЙ МАТРИЦЫ, УПРОЧНЕННОЙ ПОРОШКАМИ ПРИРОДНОГО АЛМАЗА» description=»Приведены результаты исследования влияния ультрадисперсных порошков природного алмаза на физико-механические свойства матрицы алмазного инструмента. » author=»Сафонова Мария Николаевна, Федотов Андрей Андреевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-04″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_27.06.2015_06(15)» ebook=»yes» ]

