Распад вихря – явление, широко известное и часто встречающееся как в природе (например, в явлении торнадо) так и во многих технических устройствах с закруткой потока ‑ в камерах сгорания, циклонных пылеуловителях, турбулизаторах, центробежных форсунках, возникает также в осевой области интенсивных вихрей, сходящих с концов треугольного крыла [1]. Считается, что существует три основных формы распада вихря: осесимметричный и в виде одинарной или двойной спирали [1,4,6,7,9]. Объяснение явление распада вихря можно найти в [1, 4].
Моделирование распада осесимметричного вихря выполнялось методом Годунова [3, 5] в закрученном течении воздуха в трубе. Геометрия трубы задана согласно данным приведенным в [8], где опубликованы результаты экспериментального изучения осесимметричного распада вихря, с которыми проводились сравнения результатов расчетов автора.
Математическая постановка задачи представлена в [2]. Расчеты проводились на разностных сетках с количеством ячеек 100´25; 250´25; 500´20, размер ячеек уменьшался по радиусу по направлению к оси и внешней стенке трубы.
Параметры для расчетов приняты следующие:Pвых./P0=0,975¸0,995; P0=1042399,8 Па; r0=1,1985 кг/м3; Pвых=1034060,6 Па; k=1,4; R=287,15 м2/(с2×K0); Re»104. Угол закрутки потока на входе в трубу задавался как a = arctgCq/Ö(Сr2 + Cz2) = 0o¸88o. Здесь Cq, Сr, Cz –окружная, радиальная и осевая составляющие вектора скорости C.
В результате расчетов осесимметричный распад вихря (замкнутая зона возвратного течения) первоначально был получен на сетке 100´25 ячеек (рис.1а) при Pвых./P0=0,992 и угле закрутки потока на входе в трубу равном a = 560, что соответствует углу установки лопаток направляющего аппарата 340. Полученный в расчетах «пузырь» имеет размеры около 30 см в длину и диаметр около 10 мм (рисунок 1).
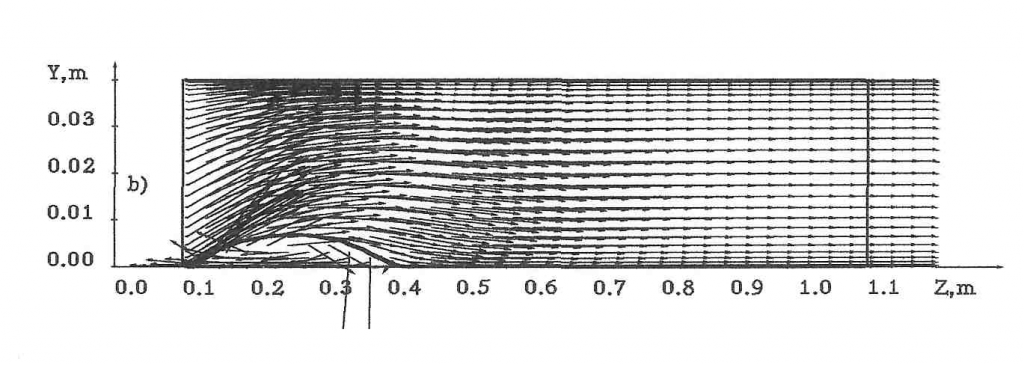
Рисунок 1. Осесимметричный распад вихря
Для изучения структуры потока при Pвых./P0=0,992 в зависимости от величины угла закрутки a на входе в трубу были проведены расчеты для углов закрутки в диапазоне a = 60o¸88o. С увеличением угла закрутки длина «bubble» (пузыря) уменьшалась, а диаметр увеличивался. При угле закрутки 88o (соответственно угол установки лопаток равен 2o) размер «пузыря» составлял в длину около 10 см, а в диаметре около 40 мм.
Влияние отношения давлений Pвых/P0 на явление осесимметричного распада вихря в трубе изучалось для Pвых/P0 в диапазоне значений 0,975¸0,995 в диапазоне a = 0o¸88°. Углы закрутки, при которых происходит первое появление «пузыря» в зависимости от отношения давлений показаны на рисунке 2. При значениях Pвых/P0 =0,975¸0,990 «пузырь» впервые появляется при углах закрутки a=50o и 49o.
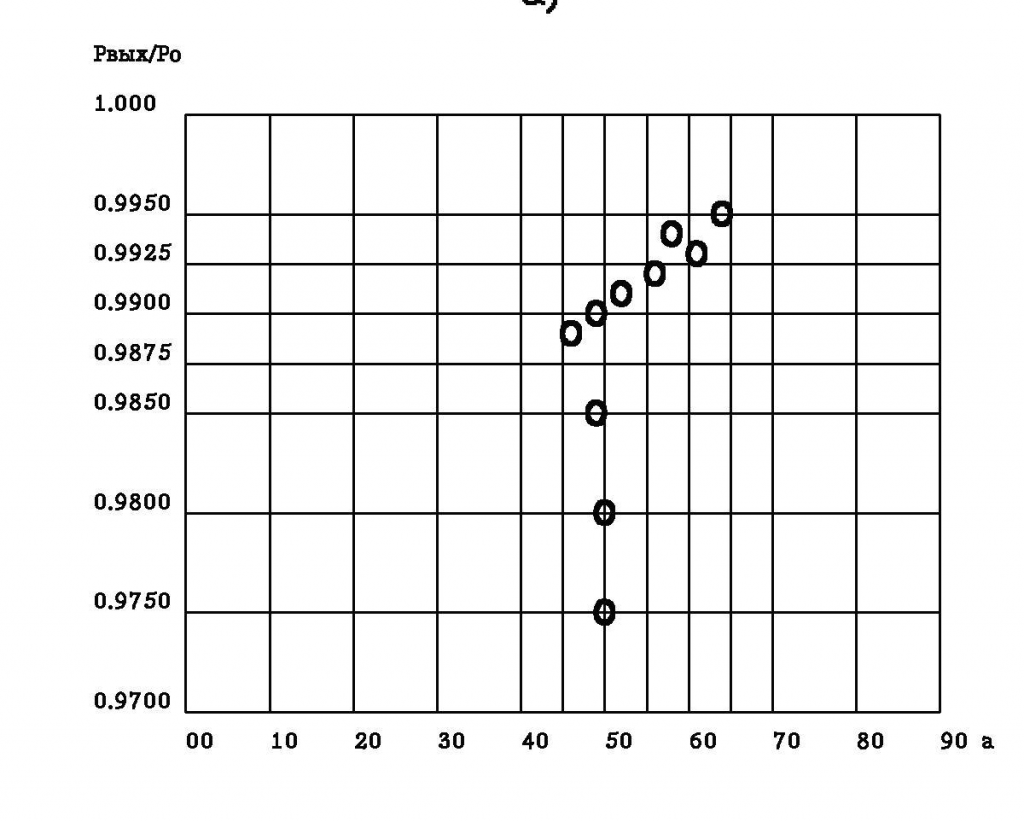
Рисунок 2. Появление «пузыря».
Изменение расхода воздуха в трубе в зависимости от угла закрутки и отношения давлений Pвых/P0 представлено на рисунке 3. Появление «пузыря» каждый раз сопровождается резким скачком повышения расхода. Величина скачка зависит от отношения давлений и уменьшается с увеличением Pвых/P0. При Pвых/P0 =0,995 и a=64o скачок увеличения расхода минимальный
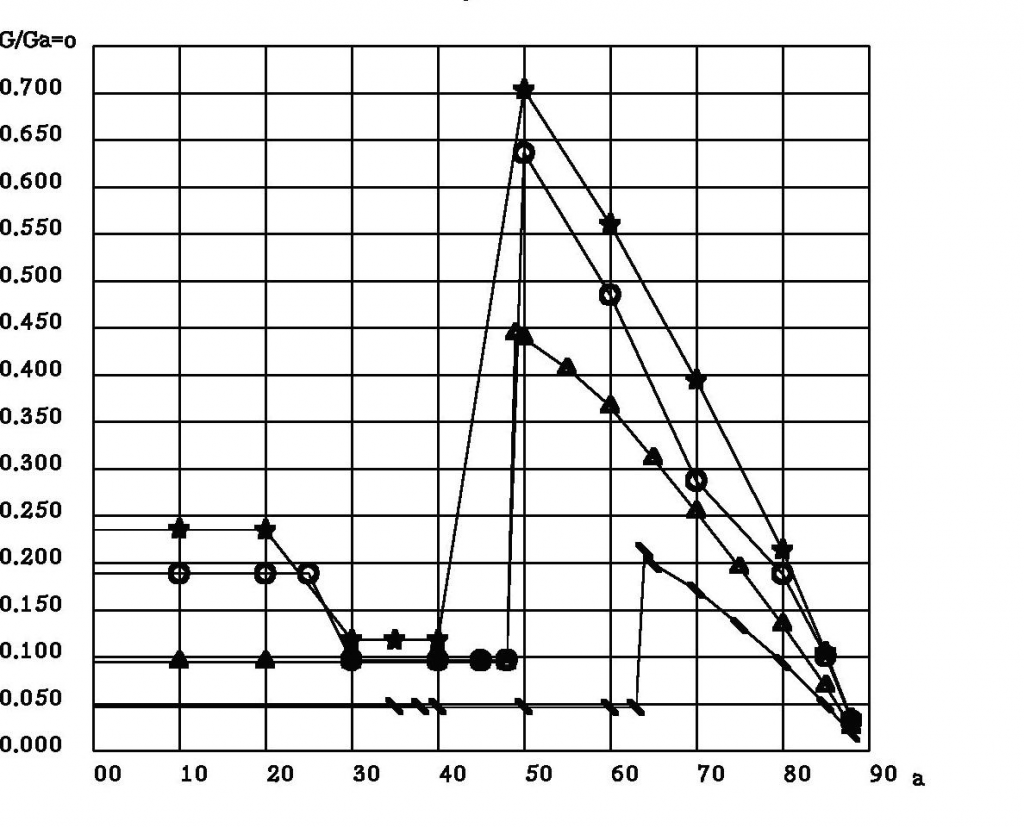
Рисунок 3. Изменение расхода G/Ga=0 в зависимости от угла закрутки a и Pвых/Pо.
‑ Pвых/P0=0,975, a=50o, ‑ Pвых/P0=0,980, a=50o,
‑ Pвых/P0=0,990, a=49o, ‑ Pвых/P0=0,995, a=64o.
Распад вихря появляется в диапазоне изменения угла закрутки 46o ¸ 64o. В эксперименте [4,9] распад вихря в воде наблюдали Harvey (1962) и Sarpkaya (1971) между 40o и 50 o закрутки. Теоретические предсказания [1,4] появления распада находятся в диапазоне углов от 45o (Squire 1960) до 62,5o (Bossel 1967). В [6] осесимметричный распад вихря получен в результате решения полных стационарных уравнений Навье-Стокса для несжимаемой жидкости в диапазоне углов закрутки 44o¸51o.
Изменение локальных параметров закрученного потока воздуха в трубе для Pвых/P0=0,990 в диапазоне углов закрутки a=100¸250, когда распад вихря в потоке отсутствует, и в диапазоне a=460¸890, когда распад вихря, «пузырь», имеет место быть, сильно отличаются. Локальные параметры для Pвых/P0=0,990, угла закрутки a=100 полученные на сетке 500х20 ячеек показаны на рисунке 4
а) б)
Рисунок 4. а) статическое давление, б) профили окружной скорости.
Локальные параметры для Pвых/P0=0,990, угла закрутки a=490 полученные на сетке 500х20 ячеек показаны на рисунке 5. Здесь приведены: а) поле векторов скорости с распадом вихря; б) изменение статического давления вдоль длины канала. Появление «пузыря» сопровождается значительным поперечным положительным градиентом давления; в) профили окружной составляющей скорости.
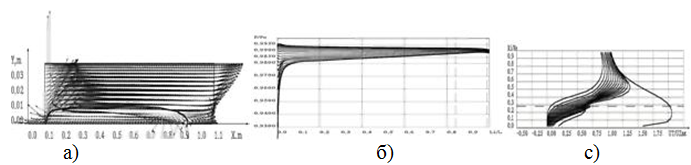
Рисунок 5. а) векторы скорости, б) статическое давление с) профили окружной скорости.
Профили осевой и окружной составляющих скорости для случая угла закрутки a=490 в сечении перед «bubble» сравнивались с экспериментальными данными, приведенными в [8]. Сравнение представлено на рисунках 6 и 7. Черные непрерывные линии – расчет автора.
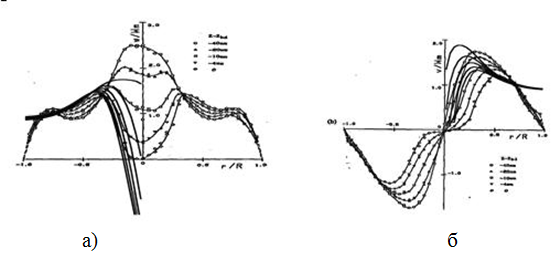
Рисунок 6. а) Профили осевой скорости: б) Профили окружной скорости.
Применение метода Годунова для моделирования осесимметричного распада вихря показало достаточно хорошее согласие с экспериментальными и численными результатами, полученными известными исследователями этого явления.
Литература
- Бэтчелор Дж. Введение в динамику жидкости. ‑ Москва: Мир, 1973.
- Высотина В.Г.//Журнал «Математическое моделирование», 2001, том 13, №10, с.103-119.
- Годунов С.К. и др// ЖВМ и МФ, 1961, т.1., № 3, с.1020‑1050.
- Гупта А., Лилли Д., Сайред Н. Закрученные потоки. – Москва: Мир, 1987.
- Дорфман Л.А. Численные методы в газодинамике турбомашин. – Л.: Энергия, 1974.
- Grabowski W.J., Berger S.AJ. Fluid Mech., vol.76, part 3, pp. 525‑544.
- Faler J.H., Leibovich S. //J. Fluid Mech., 1978, vol.86, part 2, pp.313-335.
- Shigeo Uchida, Yoshiaki Nakamura, Masataka Ohsawa.// Trans.Jap.Soc.Aeronaut. and Space Sci., 1985, 27, №78, pp.206-216.
- Turgut // J. Fluid Mech., 1971, vol.45, part 3, pp. 545-559.[schema type=»book» name=»МОДЕЛИРОВАНИЕ РАСПАДА ВИХРЯ В ТРУБЕ» description=»Моделирование осесимметричного распада вихря в трубе выполнено методом Годунова. Полученные результаты согласуются с экспериментальными данными.» author=»Высотина Вера Гавриловна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-02″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_27.06.2015_06(15)» ebook=»yes» ]

