Введение
В общей проблеме оптимального проектирования и развития систем электроснабжения (СЭС) весьма актуальными являются вопросы оптимальной трассировки сети и структуры этих систем, которые приводят к сложным многоэкстремальным задачам нелинейного дискретного программирования.
Математические модели задач этого рода могут строиться исходя из двух основных методических подходов, затрагивающих и содержательную, и математическую формулировку вопросов, а также характер приложений. Первый подход, который можно считать традиционным, заключается в сведении этих моделей к классу задач, составляющих проблему Штейнера-Вебера по построению сетей минимальной протяжённости. При этом считается заданным лишь «звездное поле» точек питания и потребления и речь идет о поиске кратчайшей связывающей их сети и одновременно генерируются дополнительные узлы разветвления этой сети (рис. 1, 2).
Такая постановка, в её чистом виде, не позволяет непосредственно учитывать планировку крупных населенных пунктов, разветвленность распределительной сети 10 – 0,4 кВ с её неоднородностью распределения нагрузки и несимметрией фазных токов, существующую сеть дорог, наличие естественных препятствий в виде рек, водоёмов и т.п. Конечно, подобные реальные ограничения на искомую электрическую сеть могут быть, в принципе, описаны в виде соответствующих дополнительных условий на размещение генерируемых узлов.
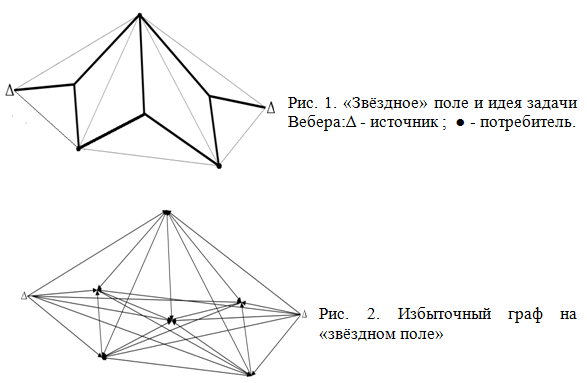
Однако, число этих условий оказывается достаточно большим даже для средних по масштабам сетей, что влечёт за собой весьма трудоёмкие затраты на подготовку конкретных расчетов.
Другой подход, рассматриваемый в данной работе, опирается на первоначальное задание (инженером-проектировщиком) исходной избыточной схемы, которая должна учитывать все фактические ограничения на плане местности и содержать все возможные и сколь угодно многочисленные (но допустимые) связи между отдельными узлами: источниками питания (ТП) и потребителями электрической энергии. Задача заключается в том, чтобы суметь отбросить («отбраковать») ненужные связи и оставить (выделить) лишь оптимальную подсеть, отвечающую наивыгоднейшему потокораспределению.
Методические основы решения задачи
Задача выбора экономически наивыгоднейшей трассировки электрической сети формулируется следующим образом.
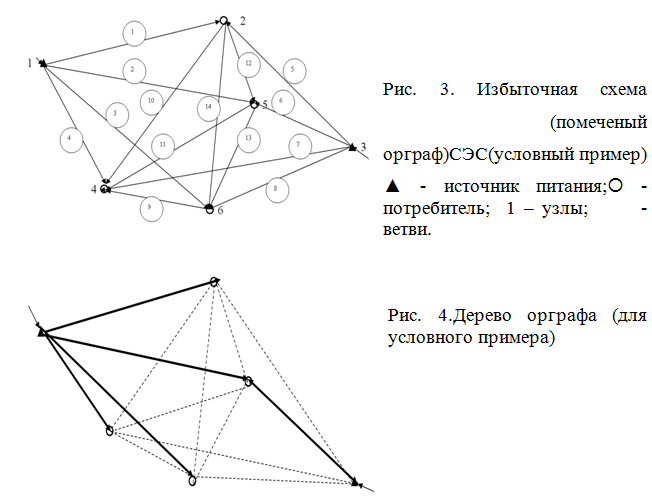
На исходной избыточной схеме сети (рис. 3), построение которой возлагается на проектировщика, заданы размещение по узлам потребителей и источников с известными величинами соответственно нагрузок и мощностей источников питания.
На первом этапе расчёта необходимо выделить на избыточной сети подсеть в виде дерева, соединяющую пункты преобразования и потребления электрической энергии таким образом, чтобы минимизировать суммарные расчетные затраты на строительство и эксплуатацию сети. Для условно принятого примера (рис. 3) выделим дерево графа (рис. 4). Для построения дерева необходимо определить количество ветвей, которые можно «отбраковать».Для условно принятого примера (для матрицы инциденций с размерностью -ветвей и линейно-независимых узлов с размерами ) количество ветвей будет равно:. Таким образом отбрасывается 9 ветвей. При этом следует отметить, что конкретизация выбора убираемых ветвей зависит от принятых критериев оптимальности.
Соответствующая математическая модель строится следующим образом. Пусть известна возможная избыточная схема (в предельном случае — это полный граф) многоконтурной электрической сети с нумерацией:

В данной модели было сделано допущение о предварительном задании величины расхода электроэнергии в системе и уровней напряжения. Практически это означает, что переменная часть эксплуатационных издержек принимается постоянной и, следовательно, решается задача на минимум капиталовложений: ![]() .
.
Система ограничений здесь состоит из условий баланса токов во всех узлах сети (первого закона Кирхгофа) и энергетического баланса для всей сети в целом, которые в матричной форме имеют вид:

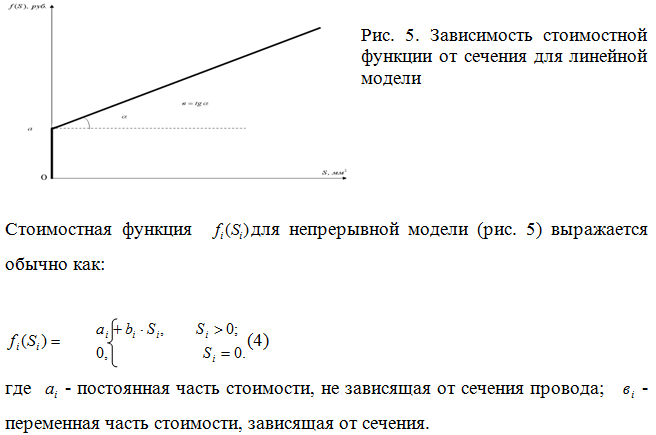

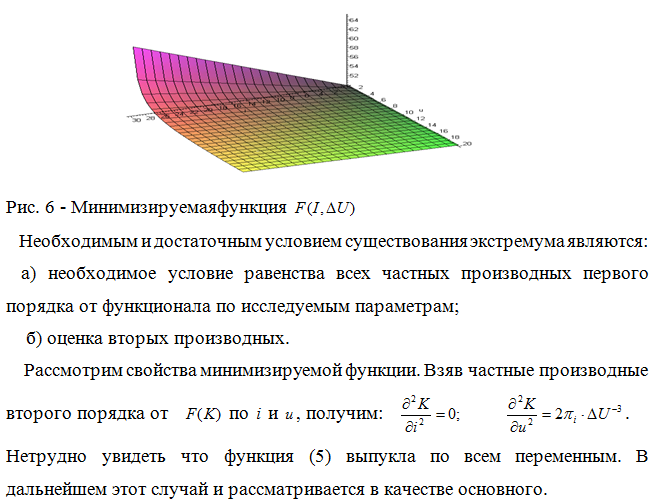



Для простоты изложения в дальнейшем рассматривается линейная зависимость между потерей напряжения и током в ветви , тогда:
![]() , (11)
, (11)
что не меняет сущности приводимых рассуждений.
В данной задаче минимизируемая функция является вогнутой, а допустимая область решений представляет собой выпуклое множество, определяемое системой линейных уравнений первого закона Кирхгофа, и поэтому речь идёт о многоэкстремальной задаче выпуклого программирования. Известно, что базисное решение такой задачи является, с одной стороны, вершиной выпуклого многогранного множества ограничений, с другой стороны – применительно к данной сетевой задаче, — одним из деревьев графа, описываемого матрицей ![]() . Поскольку локальные минимумы здесь достигаются в вершинах (угловых точках), то в нашем случае это будут деревья исходной схемы.
. Поскольку локальные минимумы здесь достигаются в вершинах (угловых точках), то в нашем случае это будут деревья исходной схемы.
Исходя из вышесказанного, и был выбран приближённый метод решения сформулированной задачи, представляющий собой модификацию метода случайного поиска исходного приближения в сочетании с локальной оптимизацией. По существу, он является методом ограниченного перебора деревьев исходной схемы и реализуется таким образом, чтобы можно было находить несколько локальных минимумов. Дерево, соответствующее меньшему из них, принимается за оптимальное.
Каждая итерация начинается с построения дерева начального приближения, удовлетворяющего заданным ограничениям материального баланса в узлах сети. Это дерево находится методом, подобным построению в сетевых транспортных задачах. Такое дерево строится для каждого из узлов схемы, выбираемого поочерёдно в качестве его корня. Для него подсчитывается первоначальное значение F*0. Затем выполняется процедура перебора соседних вариантов деревьев путём замены ветвей этого дерева хордами (участками, не вошедшими в дерево) с целью уменьшения величины F*:
для каждой хорды строится замкнутый контур, далее каждая ветвь, вошедшая в этот контур, замещается хордой путём «проведения» поконтурного расхода , равного расходу на замещаемой ветви дерева*. Вновь полученные расходы служат для вычисления нового значения F*1. Если при этом F*1 < F*0, то осуществляется переход к этому новому дереву и продолжается процедура замены ветвей дерева хордами для него. Когда для одного дерева начального приближения все хорды просмотрены указанным способом, в памяти ПК остаётся дерево с наименьшим значением F* из всех просмотренных вариантов, что означает достижение (на множестве этих вариантов) одного из локальных минимумов задачи оптимизации.
Для принятого условного примера (рис. 3) рассмотрим как изменяются хорды помеченого орграфа. С целью упрощения задачи рассмотрим одноконтурную цепь 1-2-4. Варианты хорд для выделенного дерева графа будут выглядеть следующим образом (рис.8).
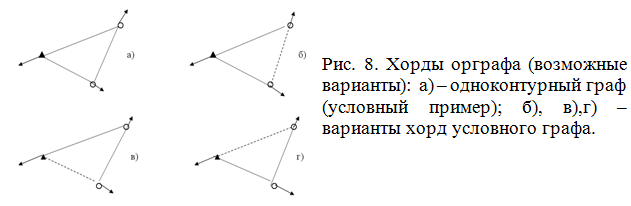
На этом заканчивается одна большая итерация. Следующая итерация начинается с построения нового дерева начального приближения и весь процесс повторяется для него.
Из полученных локальных минимумов выбирается наименьший; вариант дерева, соответствующий ему принимается в качестве оптимального решения поставленной задачи.
Данный метод является приближённым методом и существенно зависит от:
- начального приближения, которое, в свою очередь, связано с порядком перечисления участков исходной избыточной схемы;
- числа перебираемых деревьев для одного начального приближения;
- от того, как организован этот перебор;
- количества взятых начальных приближений.
Библиография
- Аренс, Хайнц, Лейтер, Юрин. Многомерный дисперсионный анализ./ Пер. с нем. и пред. В. М. Шановой и Ю. Н. Тютрина, М., Финансы и статистика, 1985 – 230 с.
- Ашманов С.А. Линейное программирование , М., Наука,1981.-340
- Берсекас Д. П. Условная оптимизация и методы множителей, М., Наука, 1982.-124 с.
- Бенке К. Методика учета неопределенности исходной информации при проектировании схем электрических сетей среднего напряжения. Автореферат.Новосибирск, 1976.[schema type=»book» name=»МАТЕМАТИЧЕСКОЕ ОБОСНОВАНИЕ ВЫБОРА ОПТИМИЗАЦИОННОЙ МОДЕЛИ ТРАССИРОВКИ ЭЛЕКТРИЧЕСКОЙ СЕТИ» description=»Целью исследования является выбор наиболее оптимального метода трассировки электрической сети на её избыточной схеме. Для достижения цели использовались методы теорииматриц, теории графов и состояний, теории цепей и теории функций комплексного переменного. Предложенновыйметодоптимизационноймоделиэлектрическойсети.» author=»Наумов Игорь Владимирович, Ямщикова Ирина Валентиновна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-21″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_25.07.15_07(16)» ebook=»yes» ]

