Введение
В настоящее время действующие нефтепродуктопроводы являются опасными производственными объектами, из которых 39 % эксплуатируются более 30 лет, а 23 % — от 20 до 30 лет. Основные фонды трубопроводного транспорта нефтепродуктов, как и вся транспортная система, стареют. В процессе их эксплуатации постепенно снижается несущая способность собственно трубопроводов. И здесь остро встают вопросы обеспечения надежности и безотказности нефтепроводов.
Одной из главных проблем остается качество изготовления труб. По существующим нормативным документам запас прочности трубопроводов определяется с учетом нагружения трубопровода внутренним давлением при условии однородного распределения напряжений по периметру и длине трубы [1]. В практике эксплуатации трубопроводных систем зафиксированы многократные случаи разрушения трубопроводов при рабочих давлениях ниже допускаемых. Причиной тому, в большинстве случаев, служит наличие в трубопроводе дефектов геометрии трубопроводов: изгибы, стыки, сопряжения труб разных размеров и локальных повреждений металла в проблемных зонах, к которым, прежде всего, следует отнести зоны сварных стыков трубопровода.
Вместе с тем, полый цилиндр является одной из наиболее распространенных геометрических форм элементов конструкций в различных областях техники. Таким образом, решение задач по определению напряженно-деформированного состояния конструкций цилиндрической формы, при наличии зон концентрации напряжений или при сложном характере их нагружения [3, 4] имеет большое научное и практическое значение.
Однако испытания полноразмерных трубных образцов достаточно сложны, требуются специфические условия для экспериментов, лабораторные модели практически невозможно изготовить из всех необходимых марок сталей, в связи с чем возникает необходимость в разработке и испытании образцов с более простой геометрией. На основании экспериментальных исследований [2] установлено, что при осевом растяжении образца с узкой двусторонней выточкой на длине участка этой выточки возникает двухосное напряженное состояние, соответствующее рабочему состоянию стенки цилиндрического сосуда при нагружении внутренним давлением. Это позволяет заменить полномасштабные трубные образцы эквивалентными им с точки зрения напряжённого состояния плоскими образцами.
Использование возможностей современной вычислительной техники и алгоритмов численного анализа, прежде всего метода конечных элементов [5, 6] позволяет исследовать проблему более детально с учетом ее специфических особенностей. Целью подобных численных экспериментов является изучение влияния различных свойств и факторов на распределение напряжений в области дефектов для различных классов сталей, а также влияние различного рода дефектов («шов» в данной работе) на НДС плоских образцов с дополнительными концентраторами, а значит, и на напряжённое состояние в области подобных дефектов в реальных трубопроводах.
Постановка задачи
В работе описан проведенный численный эксперимент исследования напряженно-деформированного состояния в области дефекта плоского образца с двумя боковыми и двумя дополнительными круговыми концентраторами. Исследовано влияние подобного дефекта на напряжённо-деформированное состояние (НДС) образца. В качестве нагружения применяется одноосное растяжение, величина которого при проведении данного численного эксперимента составляла 10 Тс.
Размеры образца без вырезов:
— длина: 300мм;
— ширина: 120мм;
— толщина: 19мм.
Параметры шва:
— длина: 60мм;
— ширина: 10мм;
— толщина: 5мм;
Рассматривается вырез в форме трапеции. Как было показано в работе по исследованию влияния формы выреза на НДС [7], целесообразнее использование дуговых концентраторов, однако более важным является изучение влияния шовного дефекта на плоские образцы в целом.
Параметры дополнительных концентраторов:
— расстояние от оси симметрии образца: 50мм;
— диаметр кругового отверстия: 35мм;
На рис. 1, 2 показана используемая в эксперименте геометрия образца без шва и со швом (грубое приближение).
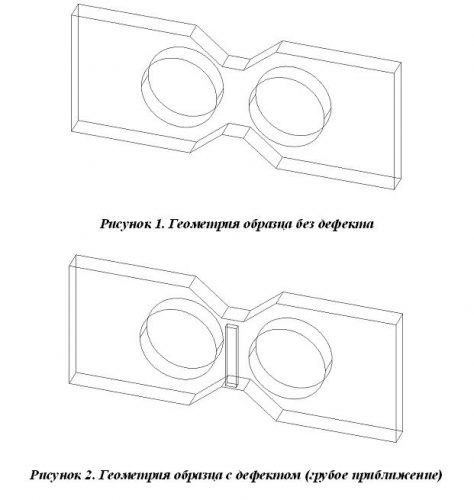
Видно, что дефект, шов, помещён в центральной области для изучения его влияния на НДС плоского образца (в центральной области создаётся двухосное напряжённое состояние). Проведенные исследования изменения состояния в центральной области, показали реальное влияние шва на состояние трубных образцов
Наличие подобного рода дефектов оказывает существенное влияние на распределение напряжений в образце [8]. Как было показано в работе [7], в отсутствии шва наблюдается плоское напряжённое состояние (с концентрацией напряжений возле вырезов), в то время как в его присутствии – объёмное напряжённое состояние, наличие серьёзных градиентов и перераспределение напряжений в центральной области, подобное возникающему в полномасштабных трубных образцах, что позволяет рассматривать плоские образцы как полноценную замену объёмным трубным образцам.
Результаты исследования
Разработан и реализован алгоритм создания адаптивной [9] конечно-элементной (КЭ) сетки [10-13]. Основная идея алгоритма – разбиение объёма образца на несколько областей, для каждой из которых выбирается тип и размер элементов, степень сгущения вблизи границ [14]. Сгущение вблизи выреза и дополнительных круговых концентраторов обусловлено наличием концентрации напряжений в этой области, тогда как сгущение в центральной части пластины и возле дефекта – наличием в этой области интересующих нас точек, в которых наблюдается с определенной точностью двухосное напряженное состояние, а также возникающих серьёзных градиентов напряжений. Вдали от концентратора, возле граней, на которых прикладывается усилие, возможно использование гораздо более крупных КЭ, поскольку здесь наблюдается равномерное напряженное состояние.
На рис. 3 показан пример используемой при проведении расчётов сетки для плоского образца с трапецеидальным вырезом и двумя дополнительными концентраторами и вариант сетки для образца с дефектом (для грубого приближения).

В первом случае возможно улучшение качества сетки с помощью сгущения в области концентрации напряжений (возле вырезов и дополнительных концентраторов). Ввиду наличия круговых вырезов достаточная простота исследуемой области образца нарушается, в связи с чем были задействованы тетраэдральные КЭ (для лучшей аппроксимации геометрии вблизи концентраторов). Стоит также учитывать влияние возможного значительного градиента напряжений в районе концентратора на выбор элемента.
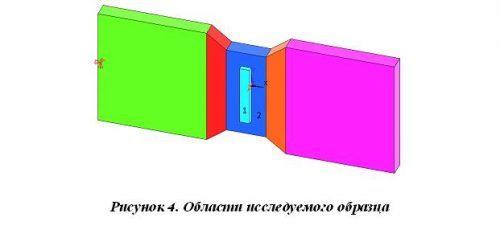
Во втором случае может быть использовано «гибридное» разбиение, в котором присутствуют как шестигранники, так и тетраэдры. Переход от шестигранной сетки к четырехгранной с привлечением пирамидальных элементов был использован для моделирования геометрии на стыке областей с разной сеткой (рис. 4, области 1 и 2). В гибридном «разбиении» используется возможность автоматической стыковки таких областей без необходимости вводить дополнительные ограничения или пропускать срединные узлы элементов и избегать разрывов в искомых функциях. Такая возможность весьма удобна, поскольку для области шва в модели строится упорядоченная сетка, тогда как область плоского образца (без шва) более сложная в геометрическом отношении (особенно в зоне концентраторов), что требует использования тетраэдральных КЭ.
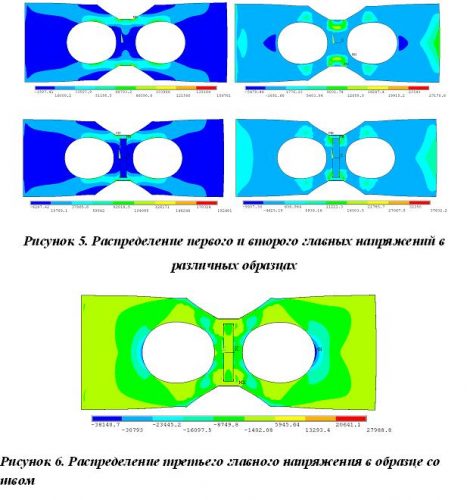
Было исследовано перераспределение напряжений в области дефекта, влияние на размер и форму области двухосного напряжённого состояния. На рис. 5 показано сравнение первого и второго главных напряжений в плоском образце и в присутствии шва (грубое приближение). Распределение третьего главного напряжения, отличного от нуля, как показано на рис. 6, даёт основание говорить об объёмном напряжённом состоянии, в отличие от реализуемого в образце без шва (плоское напряжённое состояние).
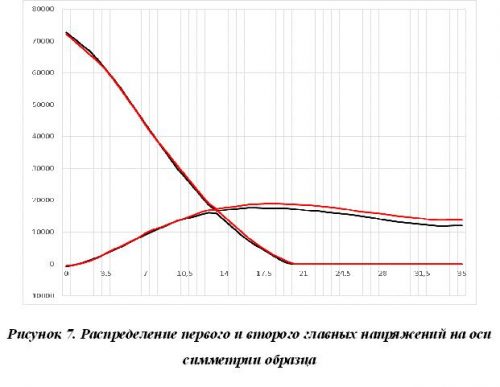
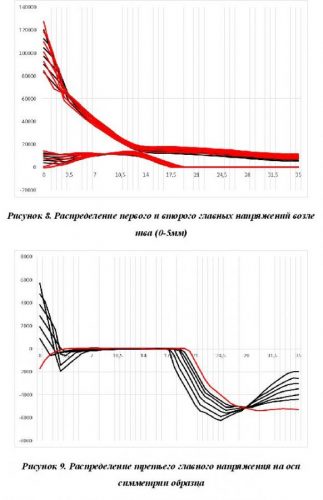
На рис. 7 показано распределение первого и второго главных напряжений на оси симметрии в образце без шва (чёрным цветом) и со швом (красным цветом); на рис. 8 – распределение первого и второго главных напряжений на расстоянии 0-5мм с шагом 1мм от шва (для образцов с дефектом, чёрным цветом) и на этом же расстоянии от оси симметрии для образца без дефекта (красным цветом).
На рис. 9 показано распределение третьго главного напряжения на оси симметрии образца со швом. Видно, что возле центра масс образца и в верхней части его, возле трапецеидального концентратора, третье напряжение отлично от нуля, т.е. наблюдается объёмное напряжённое состояние, перераспределение главных напряжений (поскольку в образце без дефекта реализуется плоское напряжённое состояние с двумя положительными главными напряжениями и третьим, равным нулю).
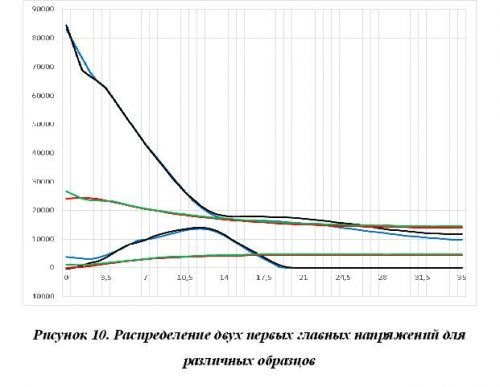
На рис. 10 показано сравнение распределения первого и второго главных напряжений в следующих образцах:
— нет шва, нет дополнительных концентраторов (красным);
— есть шов, нет дополнительных концентраторов (зелёным);
— нет шва, есть круговые концентраторы (синим);
— есть шов, есть круговые концентраторы (чёрным).
Выводы
Задача формирования геометрии компактного плоского образца требует многократного проведения численных экспериментов, для каждого из которых требуется строить свою КЭ модель. Для достижения поставленной цели был разработан алгоритм построения КЭ сетки.
Была разработана программная реализация алгоритма (язык APDL), что позволило в автоматизированном режиме перестраивать геометрию пластины в соответствии с изменениями параметров концентраторов и производить расчет, формируя файлы результатов. Приложение дает возможность оперировать с достаточно малыми шагами изменения геометрии концентраторов (для различных форм концентраторов) и автоматизировать процесс расчета и определения напряженного состояния в центральной области образца, то есть выявлять зависимости НДС от геометрии и формы концентраторов, а также влияние дефектов (типа «шов» в данной работе) на напряжённое состояние.
Показано влияние наличия дефекта «шов» на распределение главных напряжений в образце с дополнительными концентраторами. Разработанное приложение позволяет (при задании необходимой модели поведения материала дефекта) в автоматизированном режиме исследовать НДС вблизи подобных дефектов, получить аналогичные зависимости для широкого спектра отличающихся по форме и размерам локальных дефектов.
Литература
- СНиП 2.05.06–85. Магистральные трубопроводы. Госстрой СССР. – М.: ЦИТП Госстроя СССР, 1985. – 52 с.
- Подхалюзин С.З. Разработка методов повышения работоспособности магистральных трубопроводов: дисс. канд. тех. наук: 05.15.13 / С.З. Подхалюзин. – Москва, 1986. – 160 с.
- Berto, F., Lazzarin, P., Wang, C.H. Three-dimensional elastic distribution of stress and strain energy density ahead of V-shaped notches in plates of arbitrary thickness. Int. J. Fracture 127, 2004. p. 265–282.
- Lazzarin, P., Tovo, R., Blacker T.D. A unified approach to the evaluation of linear elastic stress fields in the neighbourhood of cracks and notches. Int. J. Fract. 78, 1996. p. 3–19.
- Зенкевич О.К. Метод конечных элементов в технике. – М.: Мир, 1975. – 541 с.
- Морозов Е.М., Никишков Г.П. Метод конечных элементов в механике разрушения. – М.: Наука, 1980. – 256 c.
- Царьков А.В, Пащенко В. В. Методика проведения численных экспериментов при исследовании НДС труб под давлением //Региональная научно-техническая конференция. Прикладные проблемы механики. 2014.
- Нейберг Г. Концентрация напряжений. М.: Гостехиздат, 1947, — 105 с.
- Blacker T.D., Stephenson M.B. Paving: a new approach to automated quadrilateral mesh generation. Int. Jou. Num. Meth. Eng. 32, 1991. p. 811-847.
- Бруяка В.А. Инженерный анализ в ANSYS Workbench: учебное пособие. Самара: Самарский Государственный Технический Университет, 2010, — 271 с.
- Жидков А.В. Применение системы ANSYS к решению задач геометрического и конечно-элементного моделирования. Учебно-методические материалы, Нижний Новгород, 2006, — 115 с.
- Морозов Е.М., Муйземнек А.Ю., Шадский А.С. ANSYS в руках инженера: Механика разрушения. М.: ЛЕНАНД, 2010. – 456 с.
- Чигарев А.В., Кравчук А.С., Смалюк А.Ф. ANSYS для инженеров: справочное пособие. М.: Машиностроение-1, 2004. — 512 с.
- Белкин А.Е., Гаврюшин С.С. Расчет пластин методом конечных элементов: учебное пособие. М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. — 232 с.[schema type=»book» name=»ИССЛЕДОВАНИЕ ВЛИЯНИЯ ДЕФЕКТА ТИПА «ШОВ» НА НАПРЯЖЁННО-ДЕФОРМИРОВАННОЕ СОСОТОЯНИЕ В ПЛОСКИХ ОБРАЗЦАХ ТРУБ С ДОПОЛНИТЕЛЬНЫМИ КОНЦЕНТРАТОРАМИ» description=»Предлагается решение задачи исследования влияния дефектов на напряженно-деформированное состояние (НДС) труб магистральных газопроводов с использованием компактных плоских образцов с дополнительными концентраторами в форме круглых вырезов. Разработан алгоритм проведения численного эксперимента и его реализация на языке APDL в среде ANSYS, рассмотрен один из вариантов дефектов – шов, исследовано его влияние на перераспределение напряжений, размер и форму области двухосного напряжённого состояния.» author=»Царьков Андрей Васильевич, Пащенко Василий Васильевич, Зиновьева Ольга Игоревна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-06-17″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.12.2014_12(09)» ebook=»yes» ]

