- Introduction
The roots of the cubic equation can be found by using the Cardano’s formula [3]. Unfortunately it leads to complicated analysis and optimization of the technical systems and physical objects. Nowadays the numerical simulation is widely using, so searching of the new high-speed corresponding methods is relevant.
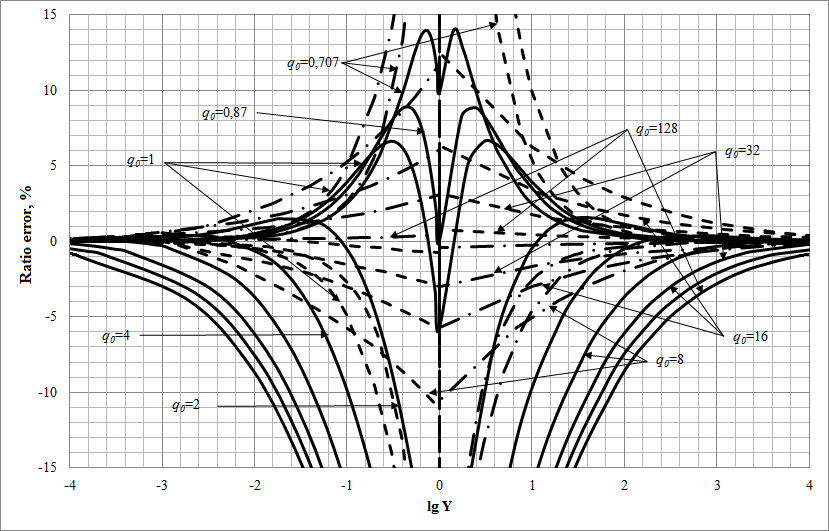
Analysis of a lot of systems leads to the cubic equations with positive coefficients, which roots are laying in the left complex half-plane. This condition evolves from Lyapunov stability [2]. In that case the relatively simple approximate formulas [4] are proposing in this article. There are also the evaluation of these formula’s errors and the method to decrease it.
- Approximate formulas
The ordinary cubic equation is represented as







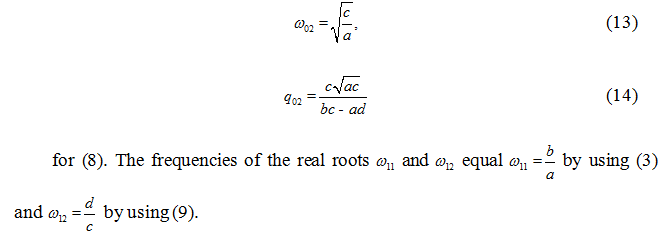


![]()



![]()
- Conclusions
There are considered the relatively simple formulas of approximate finding roots of the cubic equation with the positive coefficients and left half-plane roots in this paper. Inaccuracy estimation of given formulas is made and there are a method of their decrease. The practice worth of this approximate formulas is doubtless. So and have been used for analysis of the amplifiers frequency characteristics influence on the ARC-biquad’s parameters. As for and , it was useful for the analysis of control systems, particularly, in scanning probe microscope. Moreover, there was a program module that implements the described method and gives the opportunity to decrease the modelling computing time.
Acknowledgements
We gratefully acknowledge support from scientists of the NRNU MEPhI and its management. Authors are also thankful to the student of the NRNU MEPhI Kochetkova I.A. for invaluable help with the testing of the program that implements the described method.
References
- Benjamin C. Kuo, F. Golnaraghi, Automatic control systems, eighth ed.,Wiley, New York , 2003.
- Lyapunov A. M. (A. T. Fuller trans.), The general problem of the stability of motion, Taylor & Francis, London, 1992.
- Ronald S. Irving, Integers, polynomials, and rings: a course in algebra, Springer-Verlag, New York, 2004.
- Масленников В. В. Метод приближенного определения корней кубического уравнения с положительными коэффициентами и комплексно-сопряженными корнями // Вестник НИЯУ «МИФИ», том 4. 2015. №2. С. 179–183.[schema type=»book» name=»METHOD OF APPROXIMATE SOLVING OF THE CUBIC EQUATION WITH THE POSITIVE COEFFICIENTS » description=»The relatively simple formulas of approximate finding roots of the cubic equation with the positive coefficients and left half-plane roots are offering in this paper. Inaccuracy estimation of given formulas is made and there are a method of their decrease.» author=»Maslennikov V.V., Dovgopolaya E.A.» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-02″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_27.06.2015_06(15)» ebook=»yes» ]

