1.Введение
Во многих областях машиностроения используются трубчатые теплообменные аппараты (маслоохладители, рекуператоры, подогреватели и охладители). Большинство теплообменников в качестве первичного теплоносителя использует газ, обдувающий трубный пучок. Обдувание происходит, как правило, в поперечном направлении. Возникает потребность в исследовании особенностей обтекания тел различной формы потоком жидкости и определения силового взаимодействия между ними.
В рамках подготовки лабораторного практикума по дисциплине «Механика жидкости и газа», с целью отработки методов экспериментальных и расчётных исследований аэродинамики потока, была проведена работа по восстановлению и исследованию стенда «аэродинамическая труба». Проведено исследование поперечного обтекания цилиндрической трубки потоком воздуха.
Согласно теории [3, с. 13] поперечного обтекания цилиндра зная скорость, можно в любой точке жидкости найти давление, используя теорему Бернулли. Поскольку нам известно распределение скорости по поверхности цилиндра (1), мы можем определить давление на ней:
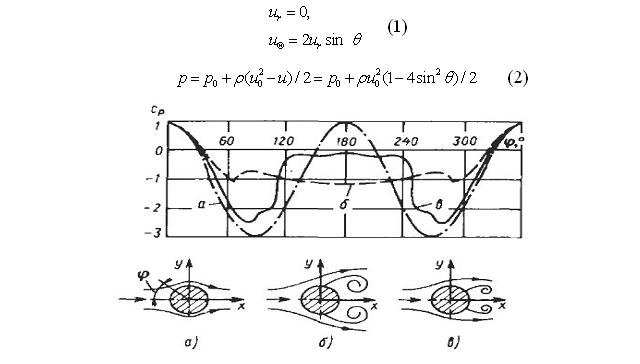
Рис.1. Распределение давления и характер линий тока для круглого цилиндра при различных числах Рейнольдса: а — идеальный, не обладающий вязкостью поток, Re→∞; б — ламинарный пограничный слой в предкритическом состоянии, Re=1,9·105; в — турбулентный пограничный слой в послекритическом состоянии, Re=6,7·105
Здесь давление на бесконечности обозначено p0. Из формулы (2) следует, что давление в лобовой точке (q = 0) превышает давление на бесконечности. Такой же величины оно достигает и в симметричной точке за цилиндром (q = p). При приближении к плоскости миделя (q = ±p /2) давление монотонно падает до величины, меньшей p0. В качестве характеристики, описывающей распределение давления, вводят коэффициент давления(3):
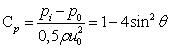 (3)
(3)
Коэффициент давления не зависит ни от радиуса цилиндра, ни от плотности жидкости, ни от скорости потока, что является одним из проявлений общего закона гидродинамического подобия.
Благодаря закону подобия, приведенную выше теорию обтекания цилиндра можно проверить экспериментально, измеряя зависимость коэффициента давления от угла q для какого-то определенного случая радиуса цилиндра, скорости набегающего потока и плотности жидкости или газа, а полученный результат будет относиться к любому случаю обтекания цилиндра.
Однако эксперименты с реальными жидкостями и газами не подтверждают формулу (3). Эксперименты показывают, что значение CP действительно равно единице в передней критической точке (q = 0), где поток разветвляется и уменьшается при приближении к плоскости миделя (q = ±p/2 ). Однако на ней коэффициент давления не падает до значения
CP=-3, как это должно бы было быть в соответствии с формулой (3), и в критической точке за цилиндром (q = p) не возрастает снова до CP=1. Это обусловлено тем, что в реальной жидкости безотрывное обтекание цилиндра, изображенное на рис.1а, невозможно. Линии тока в области p/2 <q <p отрываются от поверхности цилиндра, и в этой области образуются вихри.
2.Описание установки
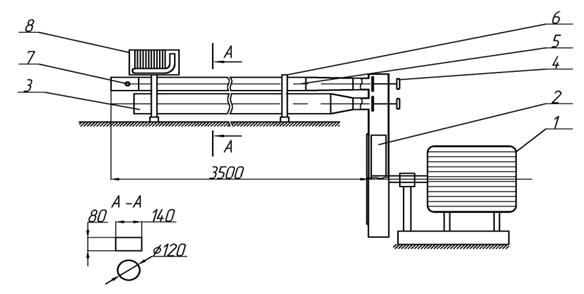
Рис. 2. Аэродинамическая труба: 1 — электродвигатель,
2 — вентилятор, 3 — байпас, 4 — регулирующее устройство,
5 — труба, 6 — опора, 7 — цилиндр, 8 – батарейный манометр
Схема установки, на которой проводились измерения, показана на рис. 2. Электродвигатель 1 вращает вентилятор 2, который нагнетает воздух в трубу 5 и байпас 3. Регулирующее устройство 4 позволяет выставить определённый расход воздуха за счёт распределения потоков между трубой и байпасом. Из основной трубы поток поступает в насадок, в котором установлен металлический цилиндр диаметром 20 мм. В цилиндре предусмотрены 12 отверстий диаметром около 1 мм для измерения значений статического давления потока вокруг цилиндра, сбором показаний служит батарейный жидкостный манометр.
3.Результаты и обработка по формулам
На основе методического руководства [6, с. 9] были произведены необходимые измерения, результаты представлены в таблице 1. При помощи трубка Пито-Прандтля находилось полное и статическое давление потока, выраженное в мм.вод.ст.. Используя формулу (4) было найдено динамическое давление потока, равное разности полного и статического давления не возмущённого потока, из которого была посчитана скорость (5).

Таблица 1
Показания батарейного манометра при различных расходах воздуха
|
Положение точки отбора, град. |
Значение Re,10-5 |
|||||
| 0,67 | 0,99 | 1,18 | 1,40 | 1,56 | 1,67 | |
|
Значение скорости, м/с |
||||||
| 10,70 | 15,13 | 18,08 | 21,40 | 23,92 | 25,57 | |
|
Отклонение жидкости от нулевого уровня в батарейном манометре по точкам отбора, мм H2O |
||||||
| 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| 30 | 3 | 6 | 10 | 12 | 15 | 20 |
| 60 | -7,5 | -15 | -22 | -30 | -37 | -44 |
| 90 | -5,5 | -11 | -16 | -22 | -26 | -32 |
| 120 | -5,5 | -11 | -16 | -22 | -26 | -32 |
| 150 | -5,5 | -11 | -16 | -22 | -26 | -32 |
| 180 | -5,5 | -11 | -16 | -22 | -26 | -32 |
Расход потока через трубу подбирался таким образом, чтоб значение показания манометра в лобовой точке было кратно 10. При анализе абсолютных значений измерений была найдена некая закономерность. Значения, полученные при 10,70 м/с были в 2 раза меньше значений полученных при скорости 15,13 м/с, и в 4 раза при 21,39 м/с. Значения при 18,08 м/с, так же в 2 раза меньше значений при 25,57 м/с. При этом, коэффициенты давления «кратных» режимов численно совпадают. Снятие показаний манометра влечёт за собой погрешность равную половине цены деления шкалы (0,5 мм). При этом она существенно влияет на значения коэффициента давления при малых расходах.
По формуле (3) были вычислены коэффициенты давления Ср, осредненное (с погрешностью в 5%) распределение коэффициента давления по окружности цилиндра представлено на рисунке 4.
Полученные для данных режимов числа Re не превышают значения
Re=1,9·105, что говорит о предкритическом состоянии течения потока, представленном на рис.1б.
4.Постановка расчета в ANSYS
Так же был произведён расчёт в программном комплексе ANSYS CFX. За расчётную модель была взята часть аэродинамической трубы, т.к. расчёт на полноценной модели показал, что поток успевает выровняться после прохождения поворотного колена и, с целью сокращения времени расчётов, в конечную модель был включён только участок трубы перед поперечно обтекаемым цилиндром длинной 0,5 м. Модель была разбита на тетраидальную сетку конечных элементов, количество элементов – 1,3Е+06. В граничных условиях задавалось полное давление на входе и статическое давление на выходе, модель турбулентности – k-Epsilon. В качестве рабочего тела был выбран воздух при 25 градусах Цельсия. Модель течения представлена на рис.3.

Рис.3. Модель течения
Из рис.3 видно, что за цилиндром образуется вихрь, происходит срыв потока, картина схожа с обтеканием цилиндра потоком в послекритическом состоянии (рис.1в).
Были произведены замеры статического давления в характерных точках на поверхности цилиндра и статического давления невозмущённого потока на расстоянии 20 диаметров от цилиндра. По формуле (3) было произведено вычисление безразмерного коэффициента давления. Результаты расчётов показали одинаковые значения безразмерного коэффициента при разных скоростях течения газа. На рисунке 4 представлено сравнение коэффициента давления полученных расчётным путём в ANSYS, экспериментально и теорией распределения давления.
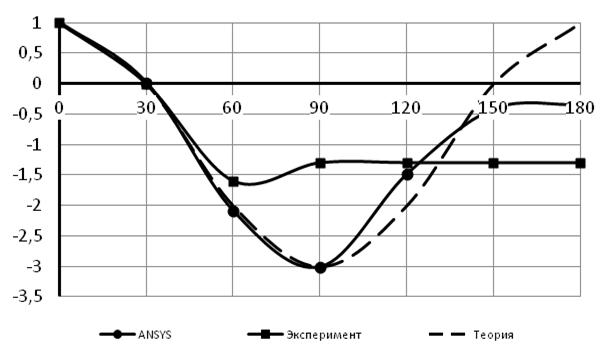
Рис.4. Распределения коэффициента давления по поверхности цилиндра
На рис.6 видно, что экспериментальные и расчётные значения коэффициента давления соответствуют теоретическому обтеканию несжимаемой жидкости на участке от 0 до 30 градусов. Далее наблюдается расхождение, связанное с режимом течения. Данные полученные расчётным путём показывают совпадение с теоретическим идеализированным обтеканием на участке от 0 до 90 градусов. Далее происходит срыв патока и данные расходятся. В эксперименте срыв происходит на 60 градусах.
Выводы
Проведена отладка экспериментального стенда, произведены все необходимые технические работы и проверки работоспособности элементов и точности показаний измерительных приборов.
В ходе постановки экспериментальной задачи большое внимание уделялось методологии проведения эксперимента, а в частности повторяемости измерений, позиционированию измерительного оборудования и исследуемого канала (обтекаемого тела). Результаты измерений хорошо коррелилруют между собой и адекватно отражают физическую модель поведения газа, обтекающего цилиндр.
Были получены значения коэффициентов давлений экспериментальным путём для потока в предкретическом состоянии. Данные полученные экспериментально совпадают с теоретическими [5, с. 106], при данном режиме течения жидкости.
Выполнено моделирование аналогичной задачи в программном комплексе ANSYS CFX, найдено значение коэффициента давления.
На передней, обращенной к потоку, стороне распределение давления в основном соответствует теоретическому распределению давления при обтекании потоком невязкой жидкости, в то время как на обратной стороне вызванное отрывом изменение структуры потока приводит к значительному снижению давления. Эпюра распределения давления относительно плоскости миделя (q = ±p/2 ) становится несимметричной.
Список литературы:
- Абрамович Г. Н. Прикладная газовая динамика. В 2 ч. Ч. 1: Учеб. Руководство: Для втузов.- 5-е изд., перераб. и доп.- М.: Наука. Гл. ред. физ.-мат. лит., 1991. – 600 с.
- Бэтчелор Дж. Введение в динамику жидкости. Пер. с англ.- М.: Мир, 1973. –792 с.
- Грязнова И.Ю., Мартьянов А.И. Экспериментальное исследование закономерностей обтекания цилиндры и крыла воздушным потоком на аэростенде ТМЖ-1М. Электронное учебно-методическое пособие. Нижний Новгород: Нижегородский госуниверситет, 2012. – 60 с.
- Мартынов А.К. Экспериментальная аэродинамика М.:ГИОП, 1950. – 479 с.
- Симиу Э., Сканлан Р. Воздействие ветра на здания и сооружения / Пер. с англ. Б.Е. Маслова, А.В. Швецовой; Под редакцией Б.Е. Маслова.-М.: Стройиздат, 1984.-360 с., ил.- Перевод. Изд.: Wind Effects on Structures / E. Simiu, R. Scanlan(1978).
- Тарасов А.В., Требухин С.А., Вульфов Е.Э. Механика жидкости и газа: Методическое руководство к выполнению лабораторных работ. Ч.2 Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2004. – 21 с.
- Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1974. 712 с.[schema type=»book» name=»РАСЧЁТНОЕ И ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ОБТЕКАНИЯ ЦИЛИНДРА В АЭРОДИНАМИЧЕСКОЙ ТРУБЕ » author=»Соболев Андрей Андреевич, Пяташов Сергей Васильевич, Неволин Александр Михайлович, Седунин Вячеслав Алексеевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-05-06″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 28.02.2015_02(11)» ebook=»yes» ]

