Известно [1, c. 32], что число обусловленности матрицы вычисляется как произведение норм исходной и обратной к ней матрицы. При очень большом числе обусловленности матрицы коэффициентов, решение соответствующей СЛАУ неточно и неустойчиво. В [2] для нахождения приближенного устойчивого решения используется регуляризация СЛАУ. Критерием устойчивости решения считается минимум нормы вектора решения; коэффициент регуляризации подбирается исходя из дополнительных соображений, например, из точности задания свободных членов СЛАУ.
В нашем случае устойчивость решения повышается посредством снижения числа обусловленности матрицы коэффициентов СЛАУ.
Квадратная матрица при решении системы СЛАУ вида


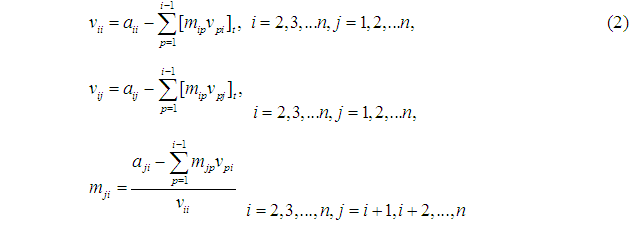

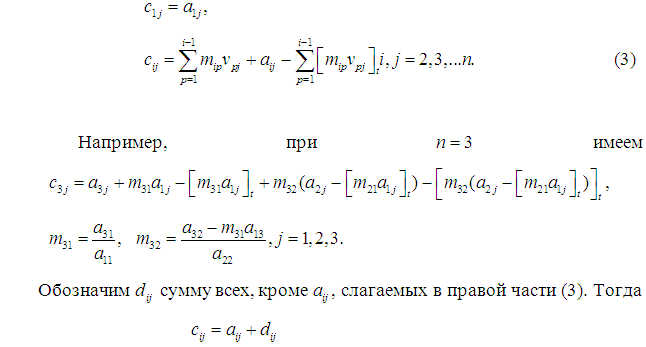




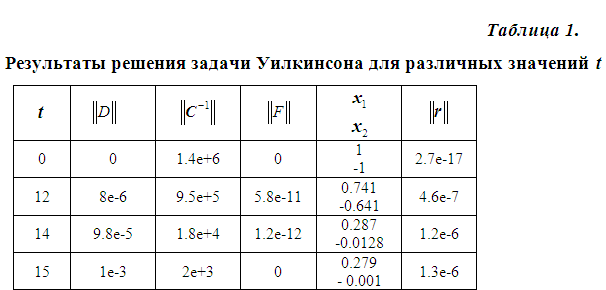

Как следует из таблицы норма матрицы с возрастанием уменьшается и решение СЛАУ с ней становится более устойчивым.
Далее рассмотрим результаты использования предложенной вычислительной схемы для матрицы Гильберта. Ее коэффициенты вычисляются согласно следующим выражениям [1,c.98]

Причиной плохой обусловленности матрицы Гильберта так же, как и матрицы Уилкинсона, является почти линейная зависимость ее строк. Нетрудно проверить, что отношение элементов строк и

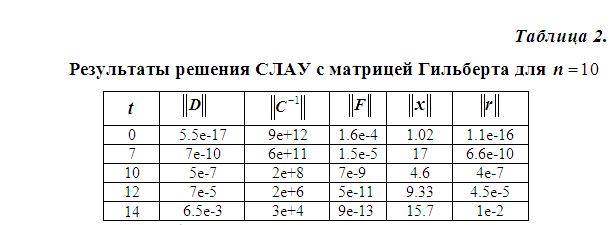
Как следует из таблицы, компромисc между точностью решения и нормой матрицы достигается при . Заметим, что в [4] эта система решалась программой повышенной точности из библиотеки SADEL, тогда как приведенные результаты получены стандартной реализацией метода Гаусса в формате double с изменением ее согласно (3).
Работа выполнена в рамках базовой части государственного задания в сфере научной деятельности проект №3442 «Информационно-алгоритмическое обеспечение систем цифрового управления, автономной высокоточной навигации и технического зрения для перспективных летательных аппаратов: разработка теоретических основ проектирования, алгоритмов, способов эффективной и надежной программной реализации, использование высокопроизводительной вычислительной инфраструктуры для экспериментального моделирования».
Список литературы
1.Дж. Форсайт, К. Моллер Численное решение систем линейных алгебраических уравнений. М.: Мир, 1969, 164 с.
2.Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. . − М.:Наука.Главная редакция физико-математической литературы, 1971. Изд. 2-е.
3.Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. − М.:Наука. Главная редакция физико-математической литературы, 1984. − 320 с.
4.SADEL-PA10. Моделирование и анализ систем и объектов. Тестирование решателей СЛАУ. URL: https://pa10.ru/?page_id=109(дата последнего обращения 20.10.2015)[schema type=»book» name=»ПРИБЛИЖЕННОЕ РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С ПЛОХО ОБУСЛОВЛЕННОЙ МАТРИЦЕЙ КОЭФФИЦИЕНТОВ» description=»Рассматривается возможность получения приближенного решения СЛАУ, у которых матрица коэффициентов плохо обусловлена. Вычислительная схема заключается в предварительной обработке исходной матрицы коэффициентов, в результате которой число обусловленности ее существенно снижается, вследствие чего полученное приближенное решение становится более устойчивым. В основе схемы лежит метод Гаусса. Приведенные результаты вычислительных экспериментов подтверждают возможность получения устойчивого приближенного решения, которое оценивается по величине невязки.» author=»Лутай Владимир Николаевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-24″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_31.10.15_10(19)» ebook=»yes» ]

