- Введение
Обычно, при проектировании конструкций из композиционных материалов, помимо локальных свойств напряженного состояния (таких как распределение напряжений, в опасных зонах, максимальные напряжения и т.д.), необходимо оценить жесткость такой конструкции в целом. Содержание задачи приведения заключается в нахождении приведенных упругих параметров армированной среды, т.е. в отыскании упругих параметров сплошной среды, обладающей той же жесткостью, что и исходная.
Существует довольно обширная литература, в которой изложены различные приближенные подходы к осреднению свойств армированных сред, использующие те или иные допущения. Такие подходы привлекательны простотой, но они не работают в более сложных случаях, например, при наличии иерархии структур, анизотропии упругих свойств компонент и т.д.
Более общий путь решения проблемы осреднения заключается в том, чтобы рассматривать ее как следствие из соответствующих краевых задач для структуры. При таком подходе метод получения макрохарактеристик среды становится нечувствительным к усложнению ее структуры, важно лишь то, что среда обладает геометрической и силовой симметрией.
- Постановка задачи
В качестве модели ВКМ примем некоторую 3-мерную изотропную кусочно-однородную среду, упругие и геометрические свойства которой неизменны в направлении х3 и имеют двоякопериодический характер в плоскости х1х2. Будем полагать, что в среде реализуется такое напряженно-деформированное состояние, при котором компонента деформации е33 не зависит от всех координат, а остальные компоненты деформации — от координаты х3.






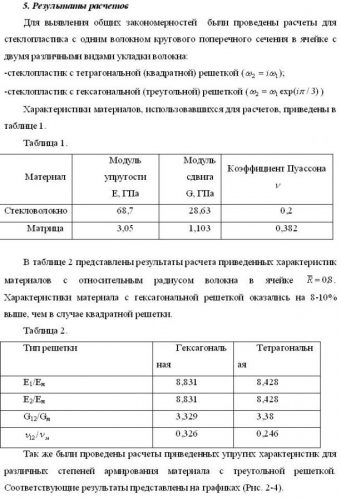
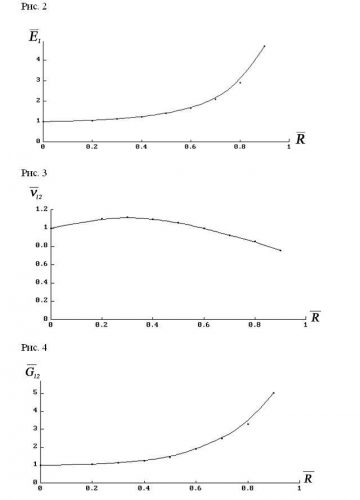
Кроме упомянутых выше материалов с правильными решетками, были проведены расчеты композитов с другими, отличными от правильных, структурами фундаментальной ячейки. Во всех случаях приведенные характеристики таких композитов при одинаковых относительных размерах армирующих волокон лежали между соответствующими значениями для тетрагональной и гексагональной ячеек. Этот факт может быть использован для определения верхней и нижней границ упругих характеристик ВКМ. При этом гексагональная схема укладки армирующих волокон представляется наиболее выгодной, кроме того, она более точно отражает реальную структуру материала.
Литература
- Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. М., Наука, 1966г., 708с.
- Григолюк Э.И., Фильштинский Л.А. Периодические кусочно-однородные упругие структуры. М., Наука, 1992г., 287с.
- Молодцов Г.А. Напряженные элементы конструкций ЛА из композиционных материалов. М., Машиностроение, 1993г., 224с.
- Косачев С.Л. Структурные остаточные напряжения в гибридных волокнистых композиционных материалах. Материалы международного научного семинара «Технологические проблемы прочности» Подольск, 2004г., с.193-198[schema type=»book» name=»ОПРЕДЕЛЕНИЕ ПРИВЕДЕННЫХ УПРУГИХ ПАРАМЕТРОВ РЕГУЛЯРНО АРМИРОВАННОГО ВОЛОКНИСТОГО КОМПОЗИЦИОННОГО МАТЕРИАЛА» author=»Косачев Сергей Леонидович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-06-12″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.12.2014_12(09)» ebook=»yes» ]

