Операторный подход при расчёте напряжённо-деформированного состояния оболочечных конструкций подразумевает исследование качественных свойств решений нелинейных моделей оболочечных конструкций. В работе [1] показано, что для достаточно широкого класса таких моделей в статическом случае строится последовательность линейных операторных уравнений вида
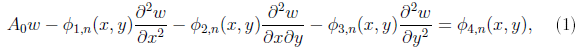
а в динамическом случае
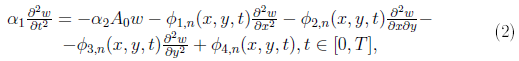
где A0 – линейный оператор (в зависимости от выбранной модели он будет меняться, например, для случая Кирхгофа – Лява это будет αΔ2, где Δ – оператор Лапласа), φi,k – некоторые функции пространства L2(Ω) в статическом случае или L∞[0,T], L2(Ω) (по соответствующим переменным) в динамическом случае.
Этот же метод можно использовать и для нахождения приближенного решения соответствующей нелинейной задачи. При этом на каждом шаге нужно решать соответствующие линейные операторные уравнения.
Последовательность решений {wn}n=1,∞ сходится в пространстве Соболева к функции прогиба w, которая является решением соответствующей нелинейной задачи. В работах [1,2] показано что такие свойства последовательности решений операторных уравнений как единственность, гладкость в зависимости от гладкости начальных условий, скорость сходимости проекционных методов к решению, переносятся на решение соответствующей нелинейной модели.
В данном докладе рассматривается вопрос применения метода Бубнова–Галёркина при решении указанных операторных уравнений при реализации операторного подхода к расчёту напряжённо-деформированного состояния оболочечной конструкции.
Рассмотрим геометрически нелинейную модель оболочечной конструкции – модель Кармана, которая в статическом случае имеет вид
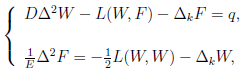
где 
– отражает гауссову кривизну деформированной серединной поверхности оболочки Ω; Δ – оператор Лапласа, 
kx и ky характеризуют кривизну поверхности оболочки Ω вдоль соответствующей оси; q – величина нормальной нагрузки, D – цилиндрическая жесткость, E – модуль Юнга.
Будем считать, что Ω – поверхность, ограниченная кривой G, и граничные условия отвечают либо жесткому, либо шарнирному закреплению краёв оболочки. Решение (w, F), где w – функция прогиба, а F – функция усилий, рассматривается в пространстве Соболева H2(Ω).
При построении операторных уравнений используем метод последовательных нагружений [3]. Представим q в виде суммы
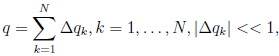
и обозначим через qn такую сумму из ровно n слагаемых. При n=1 функции (w, F) находятся в результате решения системы уравнений
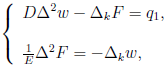
Допустим, что мы нашли решение (wn-1, Fn-1). Тогда wn ищется как решение операторного уравнения
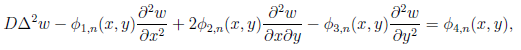
где
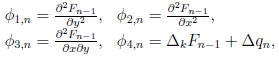
Решения последнего операторного уравнения должны удовлетворять соответствующим нулевым граничным условиям. Функция Fn ищется как решение операторного уравнения вида
В результате возникает последовательность функций {wn}. Отметим, что эта последовательность получается иным способом, чем указано в [1,2]. Но при этом также как в [1] можно показать, что эта последовательность сходится в пространстве Соболева к функции прогиба w, определяемой нелинейной системой Кармана.
Таким образом, решение системы нелинейных уравнений Кармана сводится к решению последовательности операторных уравнений указанного вида. Решение этих уравнений ищется методом Бубнова–Галёркина. В свою очередь, для применения метода Бубнова–Галёркина необходимо иметь линейно независимую систему функций из пространства, в котором действует оператор L. А для качественного анализа получаемого решения, как например в работе [4], нужно иметь ортонормированный базис пространства, в котором действует оператор L, удовлетворяющий граничным условиям задачи.
Проиллюстрируем сказанное на рассматриваемой нелинейной модели Кармана. Для определённости будем считать, что оболочечная конструкция имеет границу, составленную прямыми x=0, y=0 и кривой y=x2+1. Граничными условия зададим нулевые, что соответствует жесткому закреплению краёв оболочки
В качестве ортонормированной системы функций построим ортонормированную систему полиномов, удовлетворяющих граничным условиям. С этой целью введём вспомогательную функцию следующим образом
Определим систему функций
Для построенной таким образом системы проведём процедуру понижения размерности индекса (i,j) à (k) и получившуюся таким образом систему обозначим R. Обозначим усечение системы R до первых k2 элементов через Rk. Из построения очевидно, что для всякого положительного k система Rk будет линейно независимой.
Запишем в явном виде эту систему для k=3.
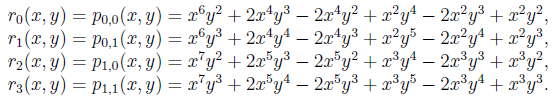
Проведём процесс ортогонализации системы Rk
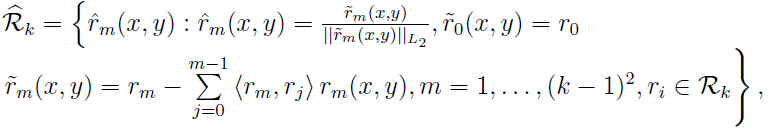
где
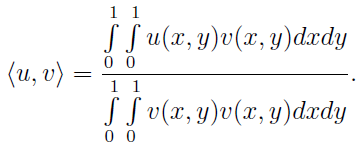
Полученная ортонормированная система удовлетворяет граничным условиям и подходит для применения метода Бубнова–Галёркина. Запишем её в явном виде:
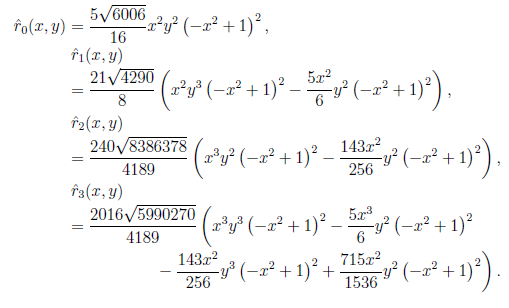
Список литературы
- Кузнецов В. Н. Метод последовательного возмущения параметров в приложениях к расчету динамической устойчивости тонкостенных конструкций : дис. … д-ра техн. наук. Саратов, 2000
- Кузнецова Т. А., Кузнецов В. Н. Ограничные полугруппы операторов и их приложения. Саратов : Изд-во Сарат. ун-та, 2004.
- Петров В. В. Метод последовательных нагружений в нелинейной теории пластинок и оболочек : Изд-во Саратовского университета, 1975. – 118 c.
- Бессонов Л. В. Численная реализация алгоритма спектрального критерия локальной потери устойчивости оболочечной конструкции // Исследования по алгебре, теории чисел, функциональному анализу и смежным вопросам : межвуз. сб. науч. Тр. – Саратов : Изд-во Сарат. ун-та, 2012. – Вып. 7. С. 3–9.[schema type=»book» name=»ОБ ОПЕРАТОРНОМ ПОДХОДЕ ПРИ РАСЧЁТЕ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ОБОЛОЧЕЧНЫХ КОНСТРУКЦИЙ» description=»В работе [1] показано, что для широкого класса нелинейных моделей оболочечных конструкций может быть построена последовательность операторных уравнений, последовательность решений которых сходится в пространстве Соболева к функции прогиба, которая является решением соответствующей модели. При нахождении решений операторных уравнений, как правило, используется метод Бубнова–Галёркина, реализация которого требует построение ортогональной системы функций, удовлетворяющих граничным условиям. В докладе показан способ построения ортонормированного базиса для решения операторных уравнений методом Бубнова–Галёркина для оболочек с произвольной конфигурацией границ.» author=»Бессонов Леонид Валентинович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-02″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_27.06.2015_06(15)» ebook=»yes» ]