- Введение
В математическом анализе важную роль играют специальные функции, которые применяются в различных приложениях и теоретических исследованиях. Среди них особую роль играет гамма-функция Эйлера, которая при задается формулой
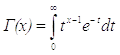 .
.
Важность этой функции определяется тем, что через неё выражается большое число определенных интегралов, бесконечных произведений и сумм рядов.
Усилия многих авторов были направлены на получение различных оценок для гамма-функции.
Так, A. Alsina и M.S Tomas в работе [1] показали, что
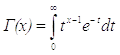
для всех x ∈ [0; 1] и неотрицательных целых .
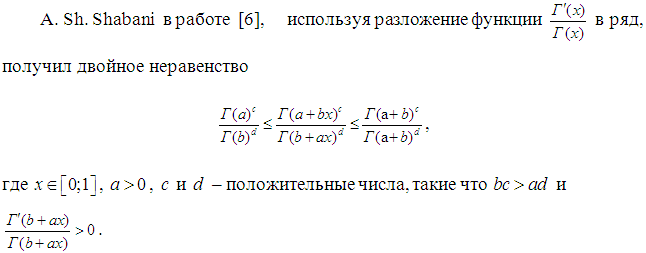
Другие интересные оценки можно найти в работах [2], [3], [5].




- Доказательство основного результата
Доказательство теоремы 1.1 проводятся по схеме, близкой к схеме, рассмотренной в работах [8], [10].

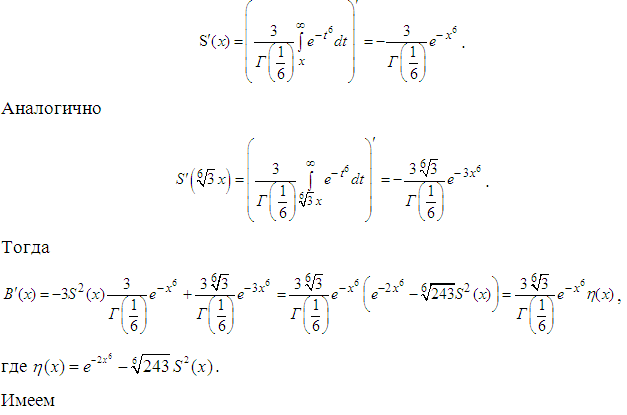



Теорема 1.1 доказана.
Список литературы:
- Alsina A., Tomas M.S. A geometric proof of a new inequality for the gamma function. J. Ineq Pure Appl.Math.6 (2005).
- Alzer H. On some inequalities for the incomplete gamma function, Math. Comp. 66 (1997), no 218, 771-778.
- Baricz A functional inequality for the survival function of the Gamma distribution, J. Inequal. Pure and Appl. Math., 9, 1 (2008), Article 13.
- Natalini P. and Palumbo B. Inequalities for the incomplete gamma function, Math. Inequal. Appl. 3 (2000), no. 1, 69-77.
- Qi F. Monotonicity results and inequalities for the gamma and incomplete gamma functions, Math. Inequal. Appl. 5 (2002), no. 1, 61-77.
- Shabani Sh. Some inequalities for the gamma function, J. Ineq Pure Appl.Math.8(2007).
- Xiao-Li Hu. Two new inequalities for Gaussian and gamma distributions, Journal of mathematical inequalities. Volume 4, Number 4 (2010), 609 – 613.
- Пекельник Н.М., Хаустова О.И., Трефилова И.А. Замечания об одном интегральном неравенстве. Х международная научно-практическая конференция: «Научные перспективы XXI века. Достижения и перспективы нового столетия» №3(10) 2015, часть 9, 72 – 74.
- Пожидаев А.В., Пекельник Н.М., Хаустова О.И., Трефилова И.А. Об оценке четных степеней срезок некоторых интегралов, Наука и мир Международный научный журнал, №1 (17), 2015, том 1, 29 – 34.[schema type=»book» name=»ОБ ОДНОМ НЕРАВЕНСТВЕ ДЛЯ НЕСОБСТВЕННОГО ИНТЕГРАЛА С ПЕРЕМЕННЫМ НИЖНИМ ПРЕДЕЛОМ» description=»В работе рассматривается несобственный интеграл первого рода с переменным нижним пределом , где — гамма- функция Эйлера. Показано, что для и выполняется интегральное неравенство . Дополнительно установлено, что это неравенство сохраняется для при положительных значениях х.» author=»Швец Юлия Владимировна, Миллер Наталья Владимировна, Пунин Роман Вячеславович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-24″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_31.10.15_10(19)» ebook=»yes» ]

