К ОЦЕНКЕ ИЗБИРАТЕЛЬНОГО ВОЗБУЖДЕНИЯ ПРИ РЕНТГЕНОСПЕКТРАЛЬНОМ ФЛУОРЕСЦЕНТНОМ АНАЛИЗЕ

Применительно к оценке относительного «чистого» вклада ε эффекта избирательного возбуждения в работах [8, 9] нами обоснован приближенный подход, в основе которого флуоресцентное излучение мешающего элемента В представлено в виде потока , испускаемого «текущим» элементарным горизонтальным слоем dy (соответственно «вниз» и «вверх») в направлении к поверхности «текущего» элементарного горизонтального слоя dx, в котором рассматривается возбуждение флуоресценции определяемого элемента А, не изотропно, а в направлении плоскости (в пределах угла от ω = 0 до ω = π/2). Так что лучи падающий первичный, флуоресценция элемента В и перпендикуляр к поверхности образца в точке падения первичного луча лежат в этой плоскости. При этом, т. к. поток флуоресценции элемента В реально распространяется (в рассматриваемом случае) по полусфере [1, 2], а мы сосредоточиваем его в названном направлении, то должны – в качестве «компенсации» – отказаться от введения традиционного сомножителя (¹/₂)∙(¹/₄_R²) (полусфера).

В [13] изотропное флуоресцентное излучение «мешающего» элемента представлено в виде ряда фиксированных направлений. Соответственно интеграл по угловой переменной заменен приближенной (квадратурной) формулой с несколькими узлами квадратурной формулы. В [14] установлено, что квадратурная формула, имеющая только один узел, обеспечивает хорошую (< 10% отн. точность). Соответственно меньше 2 % – если 3 узла, меньше 1% – если 4 узла. В [15] построены аналитические выражения для оценки эффекта избирательного возбуждения при РСФА гетерогенных порошковых образцов. Настоящая работа в определённой плоскости является развитием идей работ [13-15].

В работах [7,8] нами были получены следующие формулы.

Величина подвозбуждения «сверху»:

Таблица 1

Сопоставление рассчитанных значений ε^масс для составов С_А(Ni) = 0.1, С_В(Zn) = 0.4, С_Н = 0.5. Содержания даны в долях единицы. Значения массовых коэффициентов ослабления взяты из приложения III монографии [3].

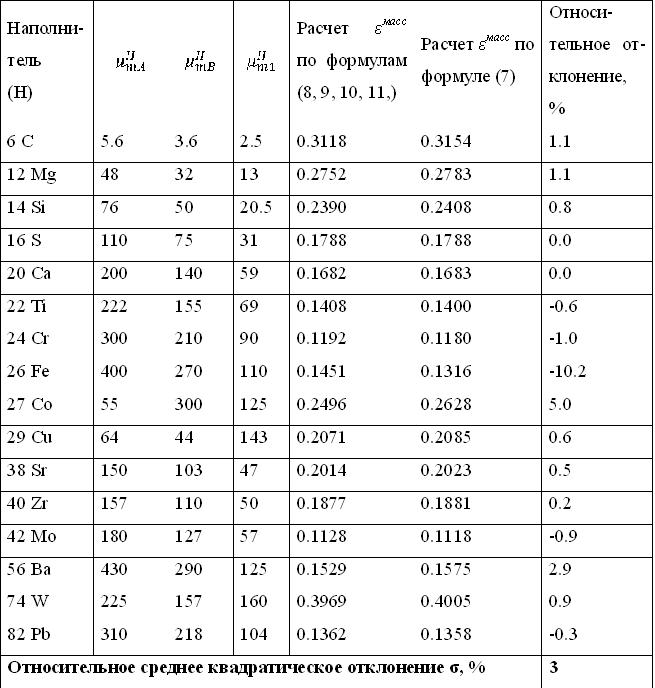
Результаты расчёта по формуле (5) для ненасыщеных образцов состава работы [9] приведены в табл. 2. Значение эффективного угла ω_эфф=32⁰ для этого расчёта получено приравниванием формулы [соотношения] (6) результату расчета ε^масс для состава С_А(Y) = 0.01, С_В(Mo) = 0.1, С_Н(SiO₂) = 0.89 массивного образца по формулам (8, 9, 10, 11). Длина волны монохроматического первичного излучения λ₁=1 Å, углы φ=ψ=45⁰.

По аналогии с работой [5], в которой градуировка РСФА плёночных образцов выполнена с использованием массивных образцов и формулы (8) [5], угол ω_эфф в случае плёночных образцов планируется устанавливать путём оценки ε^масс для соответствующих массивных образцов и применять найденное значение ω_эфф при РСФА с использованием формулы (5). Предварительные расчеты для ненасыщенных образцов подтвердили устойчивость и работоспособность формулы (5). Ниже приведен пример расчёта по формуле (5) для состава работы [9].

Таблица 2

Рассчитанные значения ε₁, ε₂ (сложением с учётом коэффициента 2МС_В) и ε^масс для состава С_А(Y) = 0.01, С_В(Mo) = 0.1, С_Н(SiO₂) = 0.89. m – поверхностная плотность образца.

m	ε₁	ε₂	ε	m	ε₁	ε₂	ε
0.01	0.035	0.036	0.071	0.25	0.290	0.473	0.763
0.02	0.066	0.070	0.136	0.26	0.292	0.479	0.770
0.03	0.093	0.103	0.196	0.27	0.293	0.484	0.777
0.04	0.118	0.134	0.251	0.28	0.294	0.489	0.783
0.05	0.139	0.163	0.302	0.29	0.295	0.494	0.789
0.06	0.158	0.191	0.349	0.3	0.296	0.498	0.794
0.07	0.175	0.217	0.392	0.31	0.297	0.501	0.798
0.08	0.190	0.241	0.431	0.32	0.298	0.505	0.802
0.09	0.204	0.264	0.468	0.33	0.298	0.508	0.806
0.1	0.215	0.286	0.501	0.34	0.299	0.510	0.809
0.11	0.226	0.306	0.532	0.35	0.299	0.513	0.812
0.12	0.235	0.325	0.560	0.36	0.300	0.515	0.815
0.13	0.243	0.342	0.585	0.37	0.300	0.517	0.817
0.14	0.250	0.358	0.609	0.38	0.300	0.519	0.819
0.15	0.256	0.373	0.630	0.39	0.301	0.521	0.821
0.16	0.262	0.387	0.649	0.4	0.301	0.522	0.823
0.17	0.267	0.400	0.667	0.41	0.301	0.523	0.824
0.18	0.271	0.412	0.684	0.42	0.301	0.525	0.826
0.19	0.275	0.423	0.698	0.43	0.301	0.526	0.827
0.2	0.278	0.433	0.712	0.44	0.301	0.527	0.828
0.21	0.281	0.443	0.724	0.45	0.302	0.527	0.829
0.22	0.284	0.451	0.735	0.46	0.302	0.528	0.830
0.23	0.286	0.459	0.745	0.47	0.302	0.529	0.831
0.24	0.288	0.466	0.754	0.48	0.302	0.529	0.831

Рисунок 2 иллюстрирует качественное согласие зависимости ε=f(m), построенной по данным табл. 2, с приведённой в работе [9].

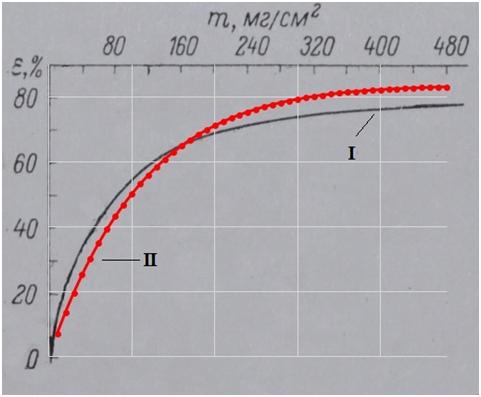
Рисунок 2. Сопоставление зависимости ε(m) настоящей работы (кривая I) и работы [3] (кривая II).

Выводы

Применительно к оценке относительного «чистого» вклада ε^масс эффекта избирательного возбуждения обоснован лучший, по сравнению с работой [8], подход для случая массивных образцов. Интегрирование по самому углу в пределах от 0 до π/2 позволило получить более точную формулу для оценки ε^масс. И при этом также не включающую угол ω.
Результаты расчета ε^масс для массивных образцов широкоизменяющегося состава согласуются с расчетом по формуле В.Ю.Залесского [3], Г.В.Павлинского и Н.Ф.Лосева [4, 5] в пределах 3%. Расчеты в случае ненасыщенных образцов также показали эффективность приближения для оценки вклада ε.
Построенное приближение для оценки вклада ε^масс (как и формула В.Ю.Залесского, Г.В.Павлинского и Н.Ф.Лосева) совершенно симметрично относительно массовых коэффициентов ослабления первичного μ_m₁ и флуоресцентного μ_mA излучения. (Поменяв μ_m₁ и μ_m_А в формуле для расчета ε^масс местами, мы ничего не изменим). Этот вывод вполне закономерен, так как вклад ε^масс избирательного возбуждения в одинаковой мере зависит от ослабления как первичного (μ_m₁), так и флуоресцентного (μ_m_А) излучения.
Простота реализации создает возможность обобщения развиваемого подхода для оценки величиныε на случай РСФА пленок на подложке, в т. ч. когда используется не только флуоресценция пленки [20], но и флуоресценция подложки [21].

Литература

Блохин М.А. Методы рентгеноспектральных исследований. М.: Физматгиз, 1959. 386 с.
Блохин М.А. Физика рентгеновских лучей. Издание 2-е, переработанное. М.:ГИТТЛ, 1957. 518 с.
Биркс Л.С. Рентгеновский микроанализ с помощью электронного зонда: пер. с англ. М.: Металлургия, 1966. 216 с.
Борходоев В.Я. Дополнительное возбуждение рентгеновской флуоресценции аналита в ненасыщенном слое с помощью подложки // Аналитика и контроль. 2015. Т. 19, № 1. С. 40-44.
Вершинина Н.В., Дуймакаев Ш.И., Чирков В.И., Вершинин А.С. Рентгеноспектральный флуоресцентный анализ многокомпонентных пленок способом теоретических поправок // Заводская лаборатория. 1983. Т. 49, № 12. С. 23 – 25.
Двайт Г. Б. Таблицы интегралов и другие математические формулы: пер. с англ. Издание четвертое. М.: Наука, 1973. 228 с.
Дуймакаев. Ш.И. Потькало М.В. Оценка избирательного возбуждения при рентгеноспектральном флуоресцентном анализе с представлением «мешающего» излучения в виде потока, испускаемого элементарным горизонтальным слоем образца в определённом «эффективном» направлении // Евразийский Союз Учёных. 2014. №8, С. 12-17.
Дуймакаев. Ш.И. Потькало М.В. К расчёту избирательного возбуждения при рентгеноспектральном флуоресцентном анализе с представлением «мешающего» излучения в виде потока, испускаемого элементарным горизонтальным слоем образца. // Евразийский Союз Учёных. 2014. №9, С. 133-136.
Залесский В.Ю. К расчету избирательного возбуждения при использовании вторичных рентгеновских спектров // Оптика и спектроскопия. 1964. Т.17, вып. 4. С. 576-582.
Лосев Н.Ф. Количественный рентгеноспектральный флуоресцентный анализ. М.: Наука, 1969. 336 с.
Мазурицкий М.И., Дуймакаев Ш.И., Скибина Л.М.. Методы РЭМ и РСФА для исследования и контроля морфологии поверхности металлополимерных пленок. // ПОВЕРХНОСТЬ. Рентгеновские, синхротронные и нейтронные исследования. 2014. № 8, с. 38 – 45.
Павлинский Г.В., Лосев Н.Ф. К оценке избирательного возбуждения рентгеновской флуоресценции в случае смешанного первичного излучения // Журнал технической физики. 1969. Т. 39, № 9. С. 1664 – 1675.
Rossiger and H.-J. Thomas, Quantitative XRF Analysis of Surface Layers: Procedure for the Determination of Thickness and Composition // X-Ray Spectrometry. 1990. V. 19, P. 211-217.
Rossiger., Validity of a Simple Approximation for Enhancement Calculations // X-Ray Spectrometry. 1992. V. 21, P. 245-247.
Финкельштейн А.Л. К расчёту интенсивности вторичной флуоресценции для порошковой среды при рентгенофлуоресцентном анализе. // Заводская лаборатория. Диагностика материалов. 1995. Т.61, №9. С. 17-21.[schema type=»book» name=»К ОЦЕНКЕ ИЗБИРАТЕЛЬНОГО ВОЗБУЖДЕНИЯ ПРИ РЕНТГЕНОСПЕКТРАЛЬНОМ ФЛУОРЕСЦЕНТНОМ АНАЛИЗЕ» description=»Развивая идеи предыдущих работ, применительно к оценке относительного «чистого» вклада εмасс эффекта избирательного возбуждения обоснован приближенный подход, в котором предпринята попытка отказа от определения ωэфф в случае массивных образцов. Построено приближение для оценки вклада εмасс Результаты моделирования подтвердили корректность и эффективность данного подхода.» author=»Дуймакаев Шамиль Исхакович, Потькало Максим Валерьевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-11″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.05.2015_05(14)» ebook=»yes» ]

euroasia

Похожие записи