Рассмотрение качественных признаков экономических систем, как правило, сопровождается изучением количественной стороны хозяйственных процессов при помощи методов математической статистики. Задача количественных исследований состоит в получении численной оценки состояния экономического процесса.
Исследования с использованием количественных методов являются основным инструментом получения информации для планирования и принятия решений. Основное преимущество количественных исследований состоит в том, что появляется возможность снижения риска принятия неправильных решений и выбора неточных параметров планирования.
Большинство исследований, связанных с использованием количественных методов в экономике – это построение моделей планирования, прогнозирования и принятия решений. Цель моделирования понять и изучить качественную и количественную природу явления, отразить существенные для исследования черты в пригодной для использования в практической деятельности форме.
В абсолютном большинстве случаев с той или иной дискретностью и формой представления, явления и процессы характеризуются некими измеряемыми или описываемыми параметрами.
Сведения об исследуемом процессе могут быть получены в виде статистических данных определенного перечня произвольно выделенных параметров, соответствующих математической модели. В процессе обработки этих сведений могут быть оценены информативность и значимость части параметров, и сформировано осознание недостаточности или избыточности первоначального перечня параметров. При этом производится и предварительная оценка достоверности и прогностической ценности математической модели.
Различают детерминированные и стохастические математические модели. В детерминированных моделях все параметры, оказывающие влияние на ответные реакции объекта исследования, однозначно определены и их значения известны в момент принятия решения. Стохастические модели предполагают наличие элемента неопределенности, учитывают возможное вероятностное распределение значений факторов и параметров, определяющих развитие ситуации.
Следует отметить, что детерминированные модели, с одной стороны, являются более упрощенными, поскольку не позволяют достаточно полно учитывать элемент неопределенности. С другой стороны, они позволяют учесть многие дополнительные факторы, зачастую недопустимые стохастическим моделям. Никакая модель не может учесть абсолютно все факторы. Профессионально разработанная модель отличается тем, что позволяет учесть наиболее существенные из них.
Очевидно, что разделение моделей на детерминированные или стохастические вполне условно, так как даже простейшие детерминированные модели можно рассматривать как стохастические при учете влияния на конечный результат случайных ошибок измерения или влияния случайных возмущений на сам процесс.
Сложность создания математической модели обычно состоит в огромном числе параметров влияния и отклика, большом числе связей между ними. Задача заключается не только в том, чтобы создать адекватное математическое описание изучаемого процесса, т.е. его модель, но и разработать методику работы с нею. С громоздкими многопараметрическими моделями трудно проводить исследования, поэтому исследователь вынужден при формализации реального процесса отбрасывать многие, реально или якобы менее существенные связи, загрублять математическое описание.
Наличие влияния заданных факторов на изучаемый процесс, отображаемый наблюдаемой статистической совокупностью экономических данных, устанавливается методами математической статистики.
В качестве примера рассмотрим оценку модели множественной регрессии, построенную с целью прогнозирования расходов бюджета Российской Федерации согласно статистическим данным показателей с 1992 года по 2015 год (таблица 1):

Таблица 1
Статистические данные по расходу бюджета РФ с млрд. рублей
|
Год |
Расход бюд
жета, y |
Расходы на обще
государственные вопросы x1 |
Расходы на национа
льную оборону x2 |
Расходы на национа
льную безопас ность и право охрани тельную деятельность x3 |
Рас
ходы на нацио нальную эконо мику x4 |
Расходы на жилищ
но – комму нальное хозяйство x5 |
Расходы на социаль но – культур ные мероп риятия x6 |
| 1992 | 6000 | 900 | 860 | 350 | 4700 | 900 | 1400 |
| 1993 | 57700 | 13000 | 7200 | 4200 | 9800 | 13000 | 14300 |
| 1994 | 230400 | 59100 | 28500 | 18100 | 10500 | 59100 | 55700 |
| 1995 | 486100 | 57700 | 49600 | 27200 | 11900 | 65200 | 129100 |
| 1996 | 652700 | 79200 | 63900 | 39200 | 17200 | 88600 | 188400 |
| 1997 | 839500 | 97900 | 81400 | 59000 | 29000 | 112600 | 270500 |
| 1998 | 842100 | 75200 | 65100 | 45400 | 31100 | 96800 | 245700 |
| 1999 | 1258 | 78,6 | 115,6 | 74,6 | 46,3 | 127,3 | 367 |
| 2000 | 1960,1 | 129 | 191,7 | 132,5 | 72,9 | 199,8 | 536,4 |
| 2001 | 2419,4 | 131,5 | 247,7 | 183,9 | 111 | 196 | 727,6 |
| 2002 | 3422,3 | 189,1 | 295,4 | 240,4 | 149 | 221,9 | 1356,8 |
| 2003 | 3964,9 | 682,5 | 355,7 | 304 | 183,2 | 254,1 | 1175,5 |
| 2004 | 4669,7 | 778,7 | 430 | 381,6 | 223 | 291,7 | 1465,5 |
| 2005 | 6820,6 | 754,3 | 581,8 | 585,2 | 764,2 | 471,4 | 3642 |
| 2006 | 8375,2 | 827,4 | 683,4 | 714,1 | 948,9 | 631,7 | 4546,4 |
| 2007 | 11378,6 | 1171,3 | 834 | 864,3 | 1558 | 1102,3 | 5822,3 |
| 2008 | 13991,8 | 1291 | 1043,6 | 1092,1 | 2258,6 | 1153,2 | 7122,1 |
| 2009 | 16048,3 | 1313,8 | 1191,2 | 1245,9 | 2782,1 | 1006,1 | 8479,6 |
| 2010 | 17616,7 | 1440,6 | 1279,7 | 1339,4 | 2323,3 | 1071,4 | 10133,8 |
| 2011 | 19994,6 | 1357 | 1517,2 | 1518,6 | 2793,4 | 1195 | 11245,9 |
| 2012 | 23174,7 | 1437,9 | 1814,1 | 1929,2 | 3273,6 | 1075 | 13215,2 |
| 2013 | 25290,9 | 1525,9 | 2105,5 | 2159,3 | 3281,7 | 1052,7 | 14678 |
| 2014 | 27611,7 | 1640,4 | 2480,7 | 2192,9 | 4543,1 | 1004,7 | 15154,2 |
| 2015 | 29741,5 | 1848,2 | 3182,7 | 2072,2 | 3774,4 | 979,9 | 17151,5 |
Согласно предпосылкам модели, случайные ошибки характеризуются постоянным разбросом или постоянной дисперсией, и данную дисперсию необходимо оценить, так как дисперсия – это характеристика влияния случайных факторов модели. Несмещенная оценка дисперсии случайных ошибок имеет вид





Проведенный расчет показал, что модель в целом значима, однако не все оценки параметра значимы. Такая ситуация является одним из признаков наличия в модели мультиколлинеарных факторов. В случае мультиколлинеарности оценки параметров модели становятся неустойчивыми.
Полученный вывод проверили, отбросив первые два и последние три наблюдения, и построили модель по «усеченной» выборке. В полученной модели оценки параметров существенно не изменились.
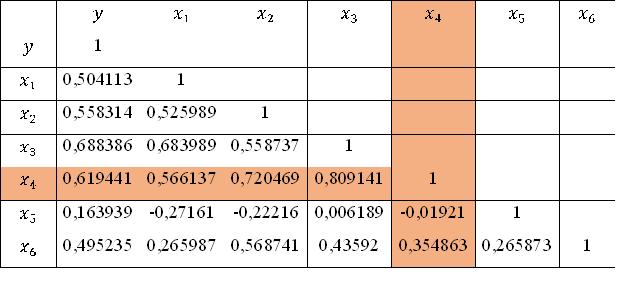
Далее проверили присутствие в модели мультиколлинеарных факторов. Для этого построили матрицу парных коэффициентов корреляции с помощью процедуры «корреляция» пакета анализа и получили таблицу 2.
Таблица 2
Матрица парных коэффициентов корреляции

Список литературы
- Бунтова Е.В. Способы анализа результатов наблюдений методами математической статистики // Инновации в науке. Новосибирск.- 2017. №1(62) С.42-50.
- Бабешко Л.О. Основы эконометрического моделирования: учебное пособие. Издание 2-е, исправленное.-М.: КомКнига, 2006.- 432 с.
- Доугерти К. Введение в эконометрику: учебник, 2-е издание, перевод с англ.-М.:ИНФРА-М.2004.-418 с.
- Ефремова Е.А. Этапы эконометрического моделирования // Экономика и менеджмент инновационных технологий. 2016. № 6 [Электронный ресурс]. URL:
- Слуцкин Л.Н. Анализ стабильности модели линейной регрессии во времени // Прикладная эконометрика. 2007. Выпуск №2.[schema type=»book» name=»ИСПОЛЬЗОВАНИЕ МЕТОДОВ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ ПРИ ПОСТРОЕНИИ ЭКОНОМИЧЕСКИХ МОДЕЛЕЙ ПРОГНОЗИРОВАНИЯ» description=»В работе представлено место и значимость использования методов математической статистики при построении моделей прогнозирования экономических показателей.» author=» Бунтова Елена Вячеславовна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-04-12″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.03.2017_03(36)_часть 1″ ebook=»yes» ]

