- Основные положения. Предлагаемая вычислительная технология решения краевых задач ориентирована на класс областей, представляющих собой объединение однородных подобластей, каждая из которых составлена из конечного числа прямоугольников с ориентацией по координатным линиям. Область может быть конструкцией, составленной из различных материалов (схема представлена в табл. 1, ее ячейки пронумерованы в соответствии с типом материала) или однородной ступенчатой областью, разбитой на непересекающиеся простые подобласти. В области решается какая-нибудь краевая задача для уравнения математической физики. Система координат в общем случае не обязана быть декартовой, тем не менее её ортогональность предполагается. В криволинейной системе область составлена из «криволинейных прямоугольников», и иллюстрация в табл. 1 в этом случае представляет собой развертку в осях криволинейной системы координат. На границах раздела подобластей ставятся условия непрерывности решения и непрерывности потока по нормали. На внешних границах ставятся обычные внешние граничные условия.
Таблица 1.
Схема неоднородной области клетчатой структуры.
| 1 | 1 | 2 | 2 |
| 3 | 4 | 2 | 4 |
| 3 | 3 | 2 | 0 |
Для приведения множества разнообразных областей к единому универсальному типу все границы раздела сред продолжаются до пересечения с границей окаймляющего прямоугольника (пунктирные линии в табл. 1), тогда в каждом случае получается кусочно-однородная область клетчатой структуры. Здесь натуральные числа обозначают принадлежность клетки к конкретной подобласти (например, это номер материала), 0 соответствует пустой клетке, лежащей вне области. Область покрывается регулярной прямоугольной сеткой, согласованной с границами подобластей.
Следующий важный шаг к универсализации технологии – это отказ от аппроксимации дифференциального уравнения на фиктивных (помеченных пунктиром) границах. Здесь точно так же, как и на реальных границах, ставятся условия баланса потоков, которые в силу полного совпадения соседних сред в действительности оказываются условиями равенства левой и правой первых производных, т. е. условиями гладкости. Их можно рассматривать в качестве вполне естественных «мягких» граничных условий. Они оказываются также естественными и в случае применения метода декомпозиции областей, когда сложная ступенчатая область разбивается на непересекающиеся более простые подобласти, обычно прямоугольники, и в результате возникают фиктивные внутренние границы сопряжения подобластей.
- Разностная аппроксимация. Предполагается, что во внутренних узлах клеток дифференциальные уравнения аппроксимируются разностной схемой на шаблоне, не более чем 3-точечном в каждом координатном направлении. Например, это может быть классическая схема второго порядка точности на 5-точечном шаблоне типа «крест» или компактная схема четвертого порядка точности на 9-точечном шаблоне типа «ящик». В основном целесообразно ориентироваться на компактные схемы четвертого порядка точности, поскольку рамки выбранного 3×3-точечного шаблона такую точность в качестве максимально возможной допускают. Известно, что на таком шаблоне существуют схемы четвертого порядка точности по пространственным переменным для уравнения Пуассона, для уравнения теплопроводности и для уравнения колебаний не только в декартовых координатах, но и в произвольной криволинейной ортогональной системе координат [2]. При этом по времени для уравнения теплопроводности порядок точности второй, а для уравнения колебаний – четвертый. В косой системе координат, когда имеются смешанные производные, на таком шаблоне для указанных уравнений не существует аппроксимаций выше второго порядка по пространству. Именно поэтому мы ограничиваемся ортогональными системами координат.
Пусть, например, внутри подобластей решение удовлетворяет уравнению теплопроводности с постоянными в пределах подобласти теплофизическими характеристиками


Разобьем слоистый пакет на части по границам раздела сред (и по фиктивным границам) и применим технологию [4], аналогичную известному методу распараллеливания прогонки, или же преобразуем задачу непосредственно локальным применением метода исключения Гаусса к обычной 3-точечной прогонке. В первом случае вначале независимо для каждого слоя решается по три вспомогательные задачи, затем из системы граничных условий находятся значения решения на границах слоев, после чего осуществляется сборка решения отдельно по каждому слою по явным простым формулам. Во втором случае сначала все граничные условия преобразуются в короткие, а затем следует классическая прогонка, сквозная по всем слоям.
После осуществления горизонтальной и вертикальной прогонки (первого и второго дробного шага) из граничных условий находится решение на гранях клеток на следующий момент времени, а затем с помощью специальных формул замыкания [3] вычисляется решение в углах клеток.
- Примеры расчетов. С применением описанной технологии по схемам различных порядков точности решались краевые задачи для уравнений различного типа. На последовательности сгущающихся сеток апостериорно оценивался практически наблюдаемый порядок точности, который обнаружил хорошее согласование с теоретическими ожиданиями.
Решалась задача для уравнения теплопроводности в составной области c отношением коэффициентов теплопроводности 1:100. Результаты по схемам различных порядков точности и их анализ приведены в работе [1].
Решалась задача Дирихле для волнового уравнения в единичном квадрате. Линия раздела сред совпадала с границей нижней левой четверти квадрата. В ней квадрат фазовой скорости (или модуль Юнга) а в остальной области . В центре нижней правой четверти квадрата задавалось сосредоточенное финитное гладкое начальное возмущение. На рисунке 1 изображены изолинии на момент времени и 3D-графики численных решений на различные моменты времени, полученные по компактной схеме четвертого порядка точности. Сплошные изолинии получены на детальной сетке 40Х40, а точками отмечены соответствующие результаты, полученные на более грубой сетке 20Х20 В табл. 2 приведена экспериментальная оценка порядка точности на сгущающихся сетках. Коэффициент убывания погрешности при дроблении сетки в два раза по временной и по обеим пространственным переменным был близок к , где – теоретический порядок точности.
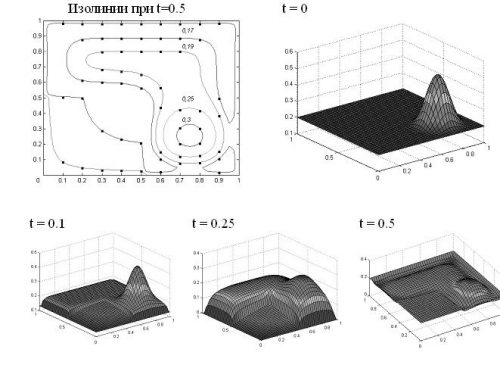
Рисунок 1. Развитие колебаний кусочно-однородной мембраны.
Таблица 2.
Погрешность в С-норме для схем различного порядка точности
|
Порядок точности |
Погрешность на сетке с шагом h | Погрешность на сетке с шагом h/2 |
Коэффициент убывания погрешности |
| 1 | 0.0609983 | 0.030879 | 1.9754 |
| 2 | 0.0198652 | 0.004979 | 3.9898 |
| 3 | 0.0053901 | 0.000678 | 7.9501 |
| 4 | 0.0038146 | 0.000240 | 15.8944 |
Рассматривалась задача о течении вязкой несжимаемой жидкости в сложной каверне (малая каверна на дне большой). Область разбивалась на три подобласти по линиям и.
На рис. 2 изображена карта изолиний функции тока, полученная по схеме четвертого порядка точности на сетке 20х20, в плоской сложной каверне, верхняя граница которой движется с единичной скоростью влево, а остальные участки границ твердые и неподвижные. В таблице 2 приведены относительные нормы ошибок для разных схем на сетках 10х10 и 20х20.

Рис. 5. Изолинии функции тока при числе Рейнольдса Re=100.
Таблица 3.
С-норма относительной ошибки для схем различного порядка точности
| Порядок точности | 1 | 2 | 3 | 4 |
| Сетка 10х10 | 0.234 | 0.107 | 0.017 | 0.0015 |
| Сетка 20х20 | 0.123 | 0.036 | 0.003 | 0.0001 |
Список литературы:.
- Ичетовкин Д.А., Паасонен В.И. Численное исследование высокоточных схем в областях клетчатой структуры // Вычислительные технологии. 2010. Т.15. № 6. С. 81-86.
- Паасонен В.И. Компактные схемы для систем уравнений второго порядка с конвективными членам // Вычислительные технологии. 1998. Т.3. № 1. С. 55-66.
- Паасонен В.И. О применении компактных схем для уравнения колебаний в кусочно-однородных средах // Вычислительные технологии. 2010. Т. 15. № 5. С. 92-98.
- Паасонен В.И. Сходимость параллельного алгоритма для компактных схем в неоднородных областях // Вычислительные технологии. 2005. Т. 10. № 5. С. 81-89.[schema type=»book» name=»ВЫСОКОТОЧНЫЕ РАЗНОСТНЫЕ МЕТОДЫ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ С ДЕКОМПОЗИЦИЕЙ ОБЛАСТЕЙ » author=»Паасонен Виктор Иванович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-06-13″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.12.2014_12(09)» ebook=»yes» ]

