Одним из важнейших направлений исследования математических дисциплин является изучение их истории, позволяющей представить основополагающие структурные части математики в развитии и взаимодействии как единого целого. Наименее исследованным с исторической точки зрения является комбинаторный анализ, в частности, одна из его ветвей – аддитивная теория разбиений. Под разбиением числа n на слагаемые, которые принято называть частями, понимают невозрастающую неупорядоченную последовательность натуральных чисел с суммой членов равной n.
Свой вклад в развитие аддитивной теории разбиений внес Джон Фредерик Вильям Гершель (John Frederick William Herschel) (1792-1871), английский астроном и физик.
Работая в области символического исчисления, Дж. Гершель заинтересовался проблемой подсчета разбиений числа. В 1850 г. он опубликовал статью [1], в которой получил формулу для подсчета разбиений числа на частей. Его метод был довольно трудным, однако до некоторой степени предвосхитил более простой способ подсчета разбиений, который позднее продемонстрировал А. Кэли.
Будучи хорошо знакомым с исчислением конечных разностей, ученый применил его и для подсчета разбиений.
Указанную работу можно разделить на две части. В первой, подготовительной, он получил при помощи конечных разностей ряд необходимых для дальнейшего изложения уравнений, во второй показал получение формул для нахождения количеств разбиений на 1, 2, 3, 4, 5 частей.
В самом начале Гершель ввел обозначения:
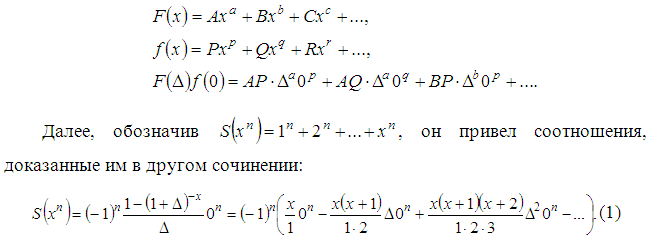

Еще одно важное соотношение имеет вид:
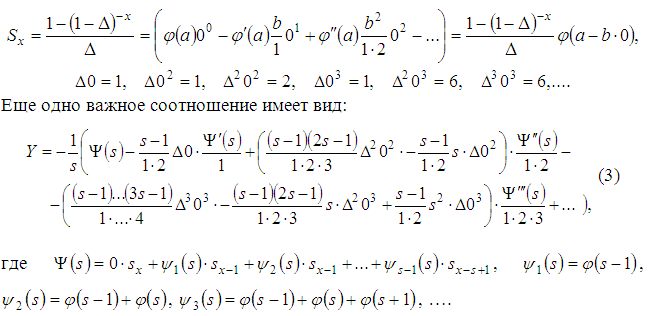









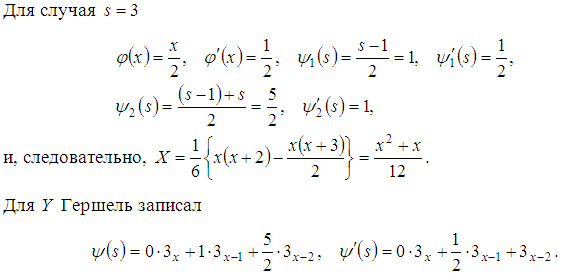
Отсюда, учитывая уравнение (3) он получил
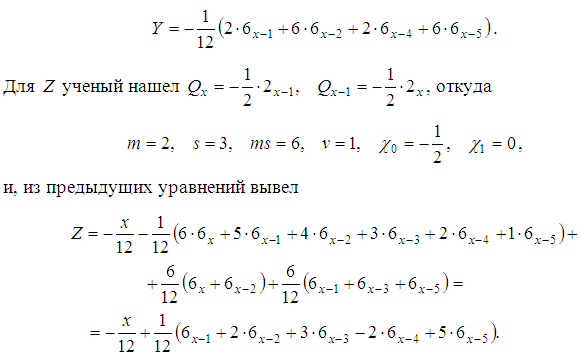
Затем он нашел

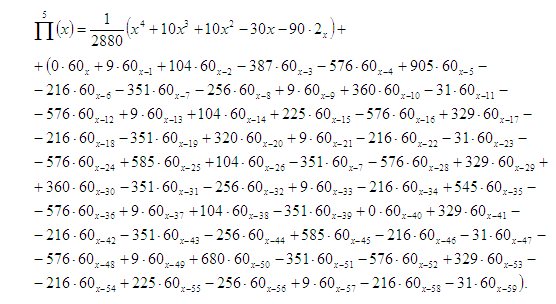

В заключении статьи Гершель отметил, что полученные им результаты аналогичны опубликованным Морганом и Г. Варбуртоном (для частей разбиения до четырех включительно).

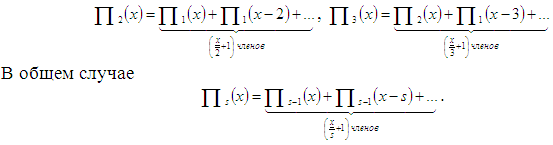
Список литературы:
- Herschel, J.F.W. On the Algebraic Expression of the number of Partitions of which a given number is susceptible / J.F.W. Herschel // Philosophical Transactions of the Royal Society of London. – 140. – Part. II. – 1850. – P. 399-422.
- Herschel, J.F.W. Philosophical Transactions of the Royal Society of London. – Т. 108. – 1818. – P. 144-168.[schema type=»book» name=» ИССЛЕДОВАНИЯ ДЖ. ГЕРШЕЛЯ ПО АДДИТИВНОЙ ТЕОРИИ РАЗБИЕНИЙ » description=»В статье рассматривается способ подсчета разбиений натурального числа, предложенный английским ученым Дж. Гершелем.» author=»Белокопытова Наталья Николаевна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-23″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_31.10.15_10(19)» ebook=»yes» ]

