В современных динамичных рыночных условиях достаточно частым колебаниям подвержены запасы ресурсов, объемы спроса, прибыль от производства товаров и услуг, изменяется технология производства. Происходящие изменения оказывают определенное влияние на значение прибылей фирм (чем больше коэффициент чувствительности, тем существеннее влияние данного параметра на конечный финансовый результат деятельности фирм), поэтому следует оперативно пересчитывать ее значение и в случае необходимости проводить соответствующую корректировку планов развития фирм с использованием коэффициентов чувствительности.
Коэффициент чувствительности представляет собой значение частной производной величины целевой функции фирмы по определенному параметру, вычисленный во внутренней точке множества устойчивости целевой функции относительно данного параметра:
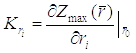, (1)
где 
– некоторый параметр экономической системы, 
– внутренняя точка множества устойчивости целевой функции фирмы относительно данного параметра.
В экономической литературе [1, c. 82-90; 2, с. 246-252] различают следующие коэффициенты чувствительности:
– коэффициент чувствительности относительно изменения некоторого элемента вектора правых частей, экономический смысл которого состоит в извлечении дополнительной прибыли при увеличении запаса данного ресурса на единицу или при увеличении спроса на соответствующий товар на единицу;
– коэффициент чувствительности целевой функции фирмы по ценовым коэффициентам, экономический смысл, которого заключается в извлечении дополнительной прибыли при увеличении удельного дохода от реализации продукции на единицу;
– коэффициент чувствительности целевой функции по элементам матрицы ограничений, экономический смысл которого означает получение дополнительной прибыли при уменьшении на единицу затрат -го ресурса при производстве единицы -го продукта.
Следует отменить, что при изменении технологии производства изменяется и удельная прибыль от производства единицы товара, поскольку изменяются затраты на закупку ресурсов. В этом случае необходимо произвести комплексное исследование на чувствительность и устойчивость как по элементам матрицы ограничений, так и по ценовым коэффициентам.
Многие экономические задачи можно описать (точно или в первом приближении) задачами линейного программирования, математическая модель которых в каноническом виде выглядит следующим образом:
При решении задачи симплекс-методом получаем оптимальное решение задачи:
По формулам (6), (7) пересчитываем значения столбца «Решение» оптимальной симплекс-таблицы и, в случае необходимости, доводим ее до оптимальной двойственным симплекс-методом.
Коэффициент чувствительности целевой функции по ценовым коэффициентам для базисных переменных определяется из приведенного вектора правых частей 
(столбец «Решение» оптимальной симплекс-таблицы) по порядковому номеру переменной в базисе; для небазисных переменных — 0 [3, с. 134-135].
При изменении ценовых коэффициентов переменных в оптимальной таблице следует изменить:
относительные оценки небазисных переменных:
Если происходит изменение ценовых коэффициентов небазисных переменных, то значение целевой функции остается прежним, и тогда достаточно пересчитать только относительные оценки этих переменных. В случае недопустимого изменения вектора ценовых коэффициентов измененную таблицу доводим до оптимальной симплекс-методом.
В случае изменения элемента технологической матрицы максимальная прибыль равна [3, с. 140-142]:
Столбцы небазисных переменных, которые не входят в В–¹ пересчитываем методом Гаусса.
Если измененная таблица и недопустима, и не оптимальна, временно удаляем ограничения, для того, чтобы выполнялось условие допустимости и далее доводим ее до оптимальной симплекс-методом. Добавляем временно удаленные ограничения и недопустимую симплекс-таблицу доводим до оптимальной двойственным симплекс-методом.
Если 
– частное изменение элемента небазисной подматрицы матрицы ограничений, то в оптимальной симплекс-таблице изменяется относительная оценка этой переменной:
. (14)
Методом Гаусса пересчитывается столбец, соответствующий этому элементу. В случае недопустимого изменения новая симплекс-таблица доводится до оптимальной симплекс-методом.
Приведем условный пример. Фирма может выпускать два вида продукции, прибыль от реализации которой, соответственно, 
. Для ее производства используются два вида ресурса, запасы которых, соответственно, 
Технологическая матрица производства имеет вид:
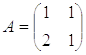
Определить оптимальный план производства и исследовать его на чувствительность при изменении запасов ресурсов, удельной прибыли от производства товаров, технологии производства.
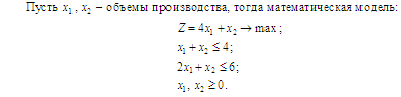
Решим задачу симплекс-методом (табл. 1).
Таблица 1
| Б | Z | X1 | X2 | S1 | S2 | Реш. | bi/aij |
Ком. |
| Z | 1 |
—4 |
-1 | 0 | 0 | 0 |
— |
не опт. |
| S1 | 0 |
1 |
1 | 1 | 0 | 4 | 4 | X1 → Б |
|
S2 |
0 |
2 |
1 | 0 | 1 | 6 |
3 |
Б → S2 |
| Z | 1 | 0 | 1 | 0 | 2 | 12 |
— |
опт. |
| S1 | 0 | 0 | 1/2 | 1 | -1/2 | 1 | — | |
| X1 | 0 | 1 | 1/2 | 0 | 1/2 | 3 | — |
Получаем неоптимальную таблицу и доводим ее до оптимальной симплекс-методом (табл. 2).
Таблица 2
| Б | Z | X1 | X2 | S1 | S2 |
Реш. |
| Z | 1 | 0 | -1/2 | 0 | 3/2 | 9 |
| S1 | 0 | 0 | 1/2 | 1 | -1/2 | 1 |
| X1 | 0 | 1 | 1/2 | 0 | 1/2 | 3 |
Доведя таблицу 2 до оптимальной, получим: Zmax = 10 – максимальная прибыль; X1 = 2, X2 = 2 – объемы производства; S1 = S2 = 0 – ресурсы расходуются полностью.
Исследование на чувствительность по элементам матрицы ограничений a13, a23, a14 и a24 не имеет экономического смысла, так как эти коэффициенты не входят в состав технологической матрицы.
Рассмотрим изменение элемента a21 (затраты второго ресурса для производства единицы первого продукта).
Измененная матрица базиса примет следующий вид:
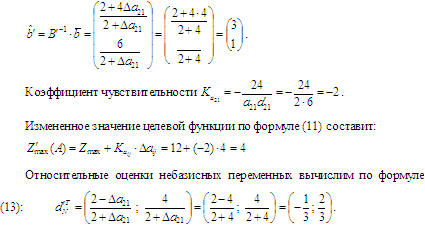
Используя метод Гаусса, пересчитываем, столбцы небазисных переменных x2 и S2, которые не входят в B¯¹. В результате измененная таблица симплекс-таблица имеет вид (табл. 3).
Таблица 3
| Б | Z | x1 | x2 | S1 | S2 |
Реш. |
| Z | 1 | 0 | -1/3 | 0 | 2/3 | 4 |
| S1 | 0 | 0 | 5/6 | 1 | -1/6 | 3 |
| x1 | 0 | 1 | 1/6 | 0 | 1/6 | 1 |
Доведя таблицу 3 до оптимальной симплекс-методом, получим: Zmax = 26/5 – максимальная прибыль, X1 = 2/5, X2 = 18/5 – объемы производства, S1 = S2 = 0 – ресурсы расходуются полностью.
В заключение отметим, что использование данной методики позволяет максимально учесть влияние рассмотренных в статье экономических переменных на целевую функцию фирм (деятельность которых можно описать математической моделью линейного программирования) и обеспечить тем самым достижение предельной коммерческой выгоды.
Список литературы:
- Федосеев В.В., Гармаш А.Н., Дайитбегов Д.М., Орлова И.В., Половников В.А. Экономико-математические методы и прикладные модели: учеб. пособие. М.: ЮНИТИ. — 391 с., 1999 – 391 с.
- Бережная Е.В, Бережной В.И. Математические методы моделирования экономических систем : учебное пособие. – М.: Финансы и статистика, 2005. –432 с.
- Сергеев П.В., Полянский А.В., Солошенко Р.В. Применение методов линейного программирования экономической теории и практике (учеб. пособие). – Изд.-во Курской государственной сельскохозяйственной академии, Курск 2015. –170 с.[schema type=»book» name=»ИСПОЛЬЗОВАНИЕ КОЭФФИЦИЕНТОВ ЧУВСТВИТЕЛЬНОСТИ ДЛЯ КОРРЕКТИРОВКИ ПЛАНОВ РАЗВИТИЯ ФИРМ» description=»В статье анализируется влияние изменения экзогенных и эндогенных переменных на целевую функцию фирм, деятельность которых можно описать моделью линейного программирования. Рассмотрены примеры корректировки планов их развития с учетом изменения запасов ресурсов, рыночного спроса, удельной прибыли от реализации товаров, технологии производства.» author=»Сергеев Петр Владимирович, Полянский Андрей Владимирович, Ковпак Оксана Владимировна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2016-12-20″ edition=»euroasia-science_28.04.2016_4(25)» ebook=»yes» ]