При необходимости определения местоположения внутри помещений, где применение глобальных систем навигации (GSM, GPS, ГЛОНАСС) невозможно или затруднено, чаще всего применяются системы Wi-Fi позиционирования. Их распространённость вызвана популярностью стандарта IEEE 802.11 (известного как Wi-Fi) при построении беспроводных локальных вычислительных сетей.
Методы Wi-Fi позиционирования можно подразделить на две группы – методы, основанные на построении модели распространения сигнала, и методы, базирующиеся на идеях теории классификации. Вторую группу методов в свою очередь зачастую разделяют на две категории – детерминистские методы и вероятностные методы. Детерминистские методы используют методы группы ближайшего соседа, вероятностные применяют теорему Байеса.
Если судить по имеющимся публикациям [2, 4, 5], методы первой группы обладают значительной погрешностью – их средняя точность составляет порядка 10 метров. В то же время применение методов второй группы позволяет добиться точности до нескольких метров [1, 3]. На практике основными методами, применяемыми при решении задачи локального позиционирования с использованием Wi-Fi сетей, являются:
- Модель Мотли-Кинана;
- Модифицированный метод k-ближайших соседей;
- Наивный байесовский классификатор.
Модель Мотли-Кинана, описанная ими в работе [4], является классической моделью распространения Wi-Fi сигнала


Экспериментальная оценка точности представленных методов производилась в демонстрационном зале компании ООО «НИИ СОКБ», план которого представлен на рисунке 1.
В качестве позиционируемого устройства был выбран смартфон LG Nexus 4, работающий под управлением операционной системы Android 4.4.
Обучающая выборка была сформирована на основании измерений уровней мощности Wi-Fi сигнала в опорных точках с шагом 4 метра. В каждой опорной точке производилось по пять измерений в четырёх направлениях.
Тестовая выборка формировалась с использованием данных того же устройства, полученных при аналогичных измерениях с разницей сутки. При этом количество точек измерений при формировании тестовой выборки было расширено с помощью тестовых точек.
Точность методов оценивалась по двум параметрам:
- Средняя ошибка позиционирования;
- Максимальная ошибка позиционирования.
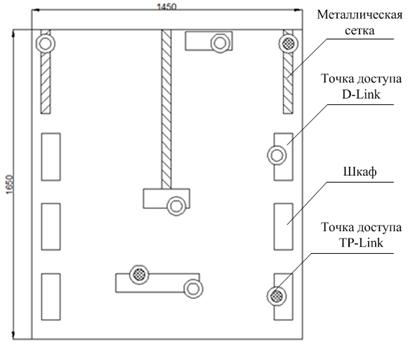
Рисунок 1. План объекта испытаний
Исследовались следующие методы:
- Модель Мотли-Кинана (базовая и модернизированная);
- Модифицированный метод k-ближайших соседей.
В рамках исследования для моделей Мотли-Кинана варьировался коэффициент, учитывающий распространение сигнала в окружающей среде; для метода k-ближайших соседей изменялись метрики расстояния и количество ближайших соседей. Результаты исследования представлены на рисунках 2 и 3.
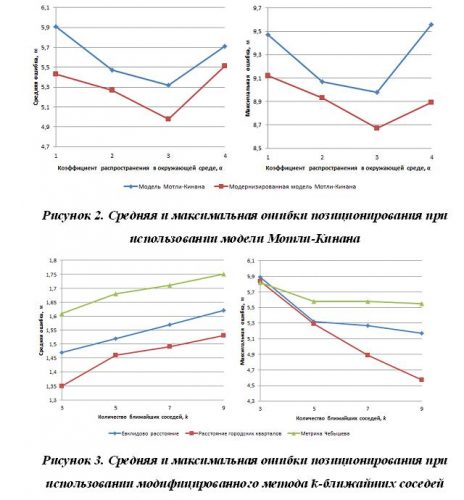
Очевидно, что наилучшие результаты с точки зрения минимизации значений ошибок каждого из методов получены при следующих настройках:
- Модернизированная модель Мотли-Кинана: α = 3.
- Модифицированный метод k-ближайших соседей: расстояние городских кварталов, k = 7.
Так как в рамках исследования метода k-ближайших соседей не были найдены настройки, при которых одновременно минимизируются как средняя, так и максимальная ошибка, то для определения наилучших результатов использовался следующий эмпирический критерий: минимальная средняя ошибка при условии, что максимальная ошибка не превышает значения 5 м.
В таблице 1 приведены общие результаты исследования точности рассмотренных методов позиционирования. Для модели Мотли-Кинана и модифицированного метода k-ближайших соседей в таблице указаны значения, полученные при использовании оптимальных настроек.
Таблица 1.
Результаты исследования точности существующих методов Wi-Fi позиционирования

Как следует из таблицы 1, ошибка позиционирования при использовании модели распространения сигнала приблизительно вдвое больше, чем при применении вероятностных методов. Из этого можно сделать вывод о том, что применение методов, основанных на построении модели распространения сигнала, для решения задачи позиционирования объектов с высокой точностью вряд ли возможно. Это обусловлено тем, что такие модели не учитывают реальную интерференционную картину Wi-Fi покрытия, на которую влияют как значительное переотражение сигналов, так и наложение их частотных спектров.
В свою очередь вероятностные методы позволяют получить приемлемую точность как с точки зрения средней, так и с точки зрения максимальной ошибок позиционирования. Именно эту группу методов можно рекомендовать для использования при построении высокоточных систем локального позиционирования.
Список литературы:
- A probabilistic approach to WLAN user location estimation. / Roos T., Myllymaki P., Tirri H., Misikangas P., Sievanen J. // International Journal of Wireless Information Networks. 2002. V. 9, N. 3. P. 155-164.
- Chen Y., Kobayashi H. Signal strength based indoor geolocation. // Proceedings of the IEEE International Conference on Communications. New York, USA. 2002. V. 1, P. 436-439
- Evennou F., Marx F. Advanced integration of Wi-Fi and inertial navigation systems for indoor mobile positioning. // EURASIP Journal on Advances in Signal Processing. 2006. P. 1-11.
- Motley A.J., Keenan J.M.P. Personal communication radio coverage in buildings at 900 MHz and 1700 MHz. // Electronics Letters. 1988. V. 24, N. 12, P. 763-764.
- Аверин И.М., Семенов В.Ю. Позиционирование пользователей с использованием инфраструктуры локальных беспроводных сетей. // Труды IV Всероссийской конференции «Радиолокация и радиосвязь». Москва, 2010. C. 474-479.[schema type=»book» name=»ЭКСПЕРИМЕНТАЛЬНАЯ ОЦЕНКА ТОЧНОСТИ СУЩЕСТВУЮЩИХ МЕТОДОВ WI-FI ПОЗИЦИОНИРОВАНИЯ ОБЪЕКТОВ» author=»Ассур Олег Сергеевич, Филаретов Геннадий Фёдорович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-06-14″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.12.2014_12(09)» ebook=»yes» ]

