Использование автоматизированного проектирования для разработки сложных конструкций, узлов и отдельных деталей позволяет уменьшить время расчетных операций, производить инженерный анализ элементов [1], увеличить производительность создания чертежей и повысить качество конструкторско-технологической документации [2].
Инструментом автоматизации решаемых пользователем задач являются пакеты прикладных программ, практически полностью освобождая исследователя от необходимости знать, как выполняет компьютер те или иные функции и процедуры по обработке информации.
В настоящее время имеется широкий спектр пакетов прикладных программ, различающихся по своим функциональным возможностям и способам реализации. В данной статье приведена последовательность расчета и произведен анализ результатов соединения деталей в системе АРМ WinMachine c использованием расчетного блока АРМ Joint [3].
|
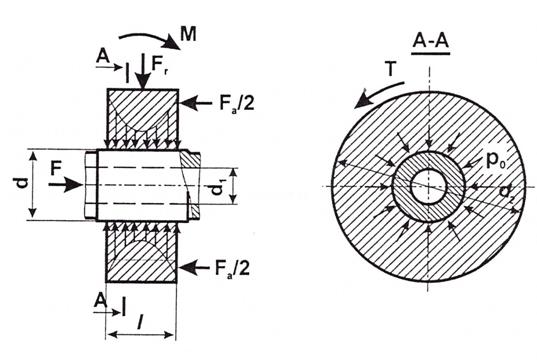
Рис. 1 — Расчет соединения с натягом по критерию несдвигаемости |
Соединения деталей при передаче вращения широко используются при проектировании деталей осесимметричной формы, которые состоят из двух или нескольких более мелких деталей. После сборки соединение должно обеспечить работу узла как единого целого. Соединение считается работоспособным, если приложенные внешние нагрузки воспринимаются им без разрушения в контакте, а возможные при этом перемещения остаются упругими.
По характеру сборки такие соединения выполняются за счет:
— использования сил трения (соединения с натягом, конические соединения, соединения коническими кольцами, клеммовые соединения);
— применения вспомогательных деталей (шпонок, штифтов, и т.п.);
— зацепления (шлицевое соединение).
Каждый из представленных типов имеет свои преимущества, недостатки и особенности, что, в конечном итоге, и определяет область его эффективного применения. Методы расчета каждого типа соединения существенно различаются.
Проанализируем соединения, воспринимающие внешнюю нагрузку за счет сил трения, создаваемых в контакте собранных деталей вследствие натяга. С помощью натяга обычно соединяют детали с цилиндрическими и коническими (реже) поверхностями контакта. Натяг достигается за счет разности посадочных размеров вала и сопряженного с ним отверстия.
Любой вид внешней нагрузки, приложенной к соединению, может быть приведен к совокупности следующих четырех силовых факторов, действующих к лежащей на оси соединения точке симметрии:
— результирующая сила , приложенная в направлении оси вращения;
— результирующий момент вращения ;
— суммарная радиальная сила ;
— суммарный момент изгиба .
Пример такого соединения для общего случая нагружения приведен на рис.1. Кривая распределения давления , возникающего на поверхности контакта вследствие натяга, рассчитана методами теории упругости [3].
Несущая способность соединения зависит как от величины, так и от характера внешней нагрузки. Например, при приложении осевой силы натяг может быть недостаточным, что приведет к сдвигу поверхностей в контакте. Для соединения это недопустимо, поэтому критерием расчета его несущей способности является отсутствие сдвига, т.е. критерий несдвигаемости. Такой же критерий используется в случае приложения момента вращения.
При расчете соединения с натягом двух деталей цилиндрической формы по критерию несдвигаемости, для того чтобы обеспечить отсутствие сдвига, необходимо, чтобы сила трения в контакте была больше, чем внешняя результирующая сдвигающая нагрузка.
Сила трения определяется по формуле,

Из неравенств (3)-(4) видно, что несущая способность соединения с натягом при заданных материалах и геометрии деталей прямо пропорциональна коэффициенту трения , поэтому результат расчета во многом зависит от правильности его выбора. Между тем задача выбора сложна, так как значение коэффициента трения зависит от многих факторов, и, прежде всего от:
— технологии сборки;
— вида материала;
— чистоты обработки поверхности и наличия погрешности формы;
— давления в контакте;
— наличия на поверхности смазки.
Обычно при расчете соединений используют среднее значение коэффициента трения. Для определения числовых значений трения можно воспользоваться данными табл.1, в которой приведены значения коэффициента трения в случае соединения с валом, изготовленным из стали.
Таблица 1 — Усредненные значения коэффициентов трения при расчете посадок с натягом
| Способ сборки соединения | Сталь | Чугун | Алюминиевые и магниевые сплавы | Латунь | Пластмассы |
|
Механический |
0,06÷0,13 | 0,07÷0,12 |
0,02÷0,06 |
0,05÷0,10 |
0,6÷0,5 |
|
Тепловой |
0,14÷0,16 | 0,07÷0,09 |
0,05÷0,06 |
0,05÷0,14 |
— |
Неравномерность распределения давления, зависящее от длины контакта, фактической геометрии деталей в соединении и погрешностей формы поверхностей сопряжения, может быть скомпенсирована за счет правильного выбора коэффициента запаса сцепления, который можно принимать равным =1,2÷1,4.
В случае переменного нагружения при выборе рекомендуется уменьшить значения ввиду ослабления натяга с течением времени.
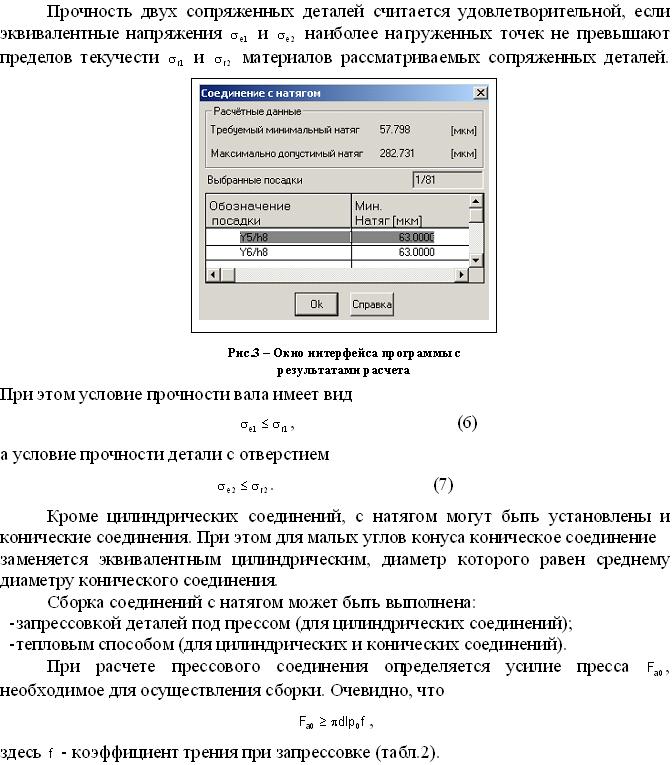
Таблица 2 — Средние значения коэффициента
трения при запрессовке
| Материал деталей соединения | |
| Сталь-сталь | 0,20 |
| Сталь-чугун | 0,14 |
| Сталь-бронза, латунь | 0,10 |
| Чугун-бронза, латунь | 0,08 |
|
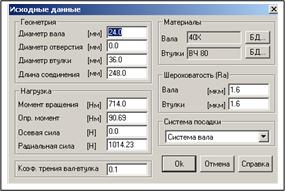
Рис.2 – Окно интерфейса программы с исходными данными |
Расчет соединения с натягом в модуле APM Joint позволяет учесть все перечисленные выше факторы, влияющие на прочность соединения [4, 5]. Для расчета, например, цилиндрического соединения в модуле APM Joint в окне «Исходные данные» задаются следующие значения (рис.2):
-геометрические параметры: диаметры вала, отверстия и втулки, а также длину соединения;
-силовые факторы, нагружающие соединение: момент вращения, опрокидывающий момент, осевую и радиальную силы;
-коэффициент трения в контакте вала с втулкой;
-материалы деталей;
-параметры шероховатости сопрягаемых поверхностей.
Указывается диапазон выбора посадок из списка «Система посадки»: все возможные, система отверстия или система вала (в примере расчета, предположим, выбирается система отверстия).
В процессе расчета программа вычисляет минимально требуемый максимально допустимый натяги, после чего производится подбор всех возможных посадок из указанного диапазона с расчетом минимальной и максимальной сил запрессовки для каждой из них. Для заданного соединения программой было подобрано посадки в системе отверстия, которые удовлетворяют условиям несдвигаемости. Некоторые результаты расчета представлены на рис.3 и в табл.3.
Таблица 3 — Результаты расчета
| Обозначение посадки | Мин. натяг [мкм] | Макс. натяг [мкм] | Мин. сила запрессовки [Н] | Макс. сила запрессовки [Н] |
| Y5/h8 | 63.00 | 105.00 | 120960.62 | 232862.59 |
| Z5/h8 | 73.00 | 115.00 | 147603.93 | 259505.83 |
| Z7/h8 | 73.00 | 127.00 | 147603.93 | 291477.81 |
| ZB5/h8 | 136.00 | 178.00 | 315456.79 | 427358.69 |
| ZB6/h8 | 136.00 | 182.00 | 315456.79 | 438016.01 |
| ZB8/h8 | 136.00 | 202.00 | 315456.79 | 491302.63 |
| ZC5/h8 | 188.00 | 230.00 | 454002.00 | 565903.90 |
Литература
- С.Г. Кондрашева, Д.А. Хамидуллина, В.А. Лашков, Вестн. Казан. технол. ун-та, 19, 193-198 (2011).
- В.М. Борисов, В.А. Лашков, С.В. Борисов, Вестн. Казан. технол. ун-та, 11, 401-405 (2010).
- В.В. Шелофаст, Основы проектирования машин. АПМ, Москва, 2005. 472 с.
- В.В. Шелофаст, Т.Б. Чугунова, Основы проектирования машин. Примеры решения задач. АПМ, Москва, 2007.240 с.
- А.А. Замрий, Проектирование и расчет методов конечных элементов в среде АРМ Structure3D. АПМ, Москва, 2010. 376 с.[schema type=»book» name=»ПРИМЕНЕНИЕ СИСТЕМЫ APM JOINT НА ПРИМЕРЕ РАСЧЕТА СОЕДИНЕНИЯ С НАТЯГОМ» description=»Рассмотрены виды соединения деталей. Приведены зависимости для расчета соединения с натягом по критерию несдвигаемости при различных нагрузках. Получены результаты расчета соединения с натягом в модуле APM Joint для расчета цилиндриче-ского соединения.» author=»Каратаев О. Р., Мухаметзянова А. А.» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-04-20″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 28.03.2015_03(12)» ebook=»yes» ]