Понятие «кратномасштабный анализ» было сформулировано в 1986 году С. Малла и И. Мейером для дискретных вейвлетов. Кратность декомпозиции сигналов с использованием дискретного вейвлет-преобразования равна двум. При использовании непрерывного вейвлет-преобразования возможен кратномасштабный анализ сигналов с кратностью меньше двух. Сокращение времени вычислений для непрерывного вейвлет-преобразования сигналов большой выборки достигается вычислением в частотной области с применением быстрого преобразования Фурье [1, 2].
Для определения средних размеров городской застройки фотографическое изображение размером 512х512 пикселей разлагается на 100 уровней и строится гистограмма распределения суммарной интенсивности J, приходящейся на каждый уровень разложения. Вычисления проверены на изображениях простых объектов, имеющих практически одинаковые размеры (рисунок 1), и на изображениях фракталов (рисунок 2). В обоих случаях в распределении интенсивности в зависимости от уровня разложения объектов присутствуют пиковые значения интенсивности, соответствующие характерным размерам элементов изображения.
Рисунок 1. Изображение простых объектов и распределение
интенсивности в зависимости от уровня разложения изображения
Для распределения интенсивности в зависимости от уровня разложения изображения фрактала характерны пиковые значения, соответствующие предфракталу n-го поколения и равноотстоящие друг от друга. Уровень пиковых значений определяется типом фрактала. Средний размер объектов (элементов изображения) D вычисляется по формуле
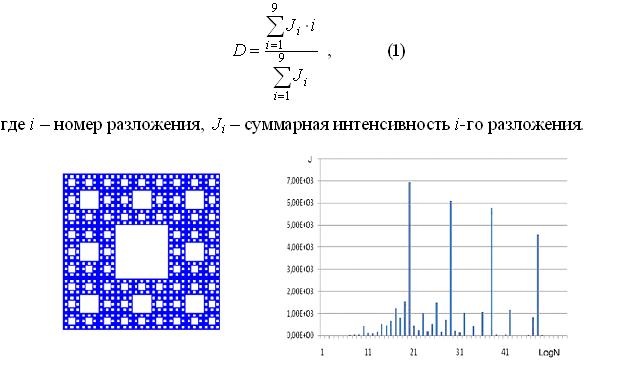
Рисунок 2. Изображение фрактала (ковра Серпинского) и распределение интенсивности в зависимости от уровня разложения изображения
Вычисление по формуле (1) дает средний размер объектов в логарифмическом масштабе. Основание логарифма вычисляется из соотношения
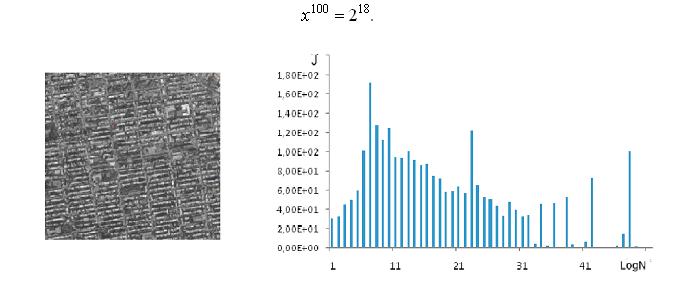
Рисунок 3. Изображение части города Нью-Йорк (США) и распределение интенсивности в зависимости от уровня разложения изображения
Средний размер объектов в масштабе изображения определяется выражением
![]()
На рисунке 3 представлено изображение фрагмента фотоснимка города Нью-Йорк (США), полученного с космического спутника, и распределение интенсивности в зависимости от уровня разложения данного изображения. В распределении интенсивностей явно выделяются пики, соответствующие предфракталу n-го поколения. Вычисления среднего размера сооружений, представленных на фотоснимке, дают результат, равный 115 метрам.
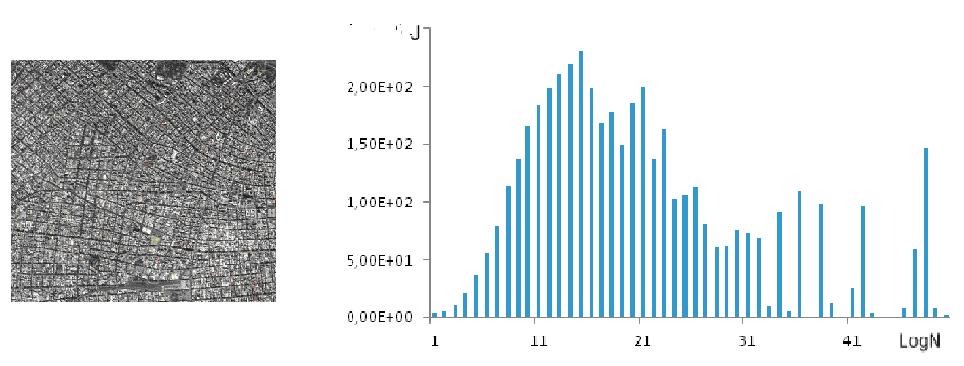
Рисунок 4. Изображение части города Буэнос-Айрес (Аргентина) и распределение интенсивности в зависимости от уровня разложения изображения
Аналогичные вычисления для города Буэнос-Айрес (рисунок 4) дают средний размер сооружений, равный 91 метру.
Список литературы
- Желтов П.В., Семенов В.И., Шурбин А.К. Применение непрерывного быстрого вейвлет-преобразования для обработки изображений. / Materiali VIII miedzynarodowej naukowi-praktycznej konferncji. Przemysl: Nauka i studia, 2012. С. 65-69.
- Семенов В.И. Свидетельство о государственной регистрации программы для ЭВМ № 2010616103. Непрерывное сверхбыстрое вейвлет-преобразование. Зарегистрировано в Реестре программ для ЭВМ 16 сентября 2010 г.[schema type=»book» name=»ПРИМЕНЕНИЕ БЫСТРОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ ДЛЯ АНАЛИЗА РАЗМЕРОВ ОБЪЕКТОВ НА ИЗОБРАЖЕНИИ» description=»Представлены результаты анализа размеров элементов городской застройки, полученные посредством непрерывного быстрого вейвлет-преобразования космических снимков городского ландшафта. По сравнению с прямым численным интегрированием скорость вычисления увеличивается на несколько порядков за счет вычисления в частотной области.» author=»Семенов Владимир Ильич, Чучкалов Сергей Иванович, Шурбин Александр Кондратьевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-25″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_31.10.15_10(19)» ebook=»yes» ]

