PID-регуляторы, описанные выше, имеют плохие показатели качества при управлении нелинейными и сложными системами, а также при недостаточной информации об объекте управления. Характеристики регуляторов в некоторых случаях можно улучшить с помощью методов нечеткой логики, нейронных сетей и генетических алгоритмов. Перечисленные методы называют «soft-computing», подчеркивая их отличие от «hard-computing», состоящее в возможности оперировать с неполными и неточными данными. В одном контроллере могут применяться комбинации перечисленных методов (фаззи- PID, нейро- PID, нейро-фаззи- PID регуляторы с генетическими алгоритмами).
Основным недостатком нечетких и нейросетевых контроллеров является сложность их настройки (составления базы нечетких правил и обучения нейронной сети) [1].
Нечеткое управление (управление на основе методов теории нечетких множеств) используется при недостаточном знании объекта управления, но наличии опыта управления им, в нелинейных системах, идентификация которых слишком трудоемка, а также в случаях, когда по условию задачи необходимо использовать знания эксперта. Примером может быть доменная печь или ректификационная колонна, математическая модель которых содержит много эмпирических коэффициентов, изменяющихся в широком диапазоне и вызывающих большие затруднения при идентификации. В то же время квалифицированный оператор достаточно хорошо управляет такими объектами, пользуясь показаниями приборов и накопленным опытом.
PID -регуляторы с нечеткой логикой в настоящее время используются в коммерческих системах для наведения телекамер при трансляции спортивных событий, в системах кондиционирования воздуха, при управлении автомобильными двигателями; для автоматического управления двигателем пылесоса и в других областях.
Поскольку информация, полученная от оператора, выражена словесно, для ее использования в PID -регуляторах применяют лингвистические переменные и аппарат теории нечетких множеств, который был разработан Л. Заде [Zadeh] в 1965 году. Основная идея этой теории состоит в следующем. Если в теории четких множеств некоторый элемент (например, температура 500 C) может принадлежать множеству (например, множеству «температура горячей воды Tгоряч.») или не принадлежать ему, то в теории нечетких множеств вводится понятие функции принадлежности, которая характеризует степень принадлежности элемента множеству. При этом говорят, например, «температура 500 C принадлежит множеству Tгоряч. со степенью принадлежности 0,264″. Функцию принадлежности можно приближенно трактовать как вероятность того, что данный элемент принадлежит множеству.
В 1974 году Мамдани [Mamdani] показал возможность применения идей нечеткой логики для построения системы управления динамическим объектом, а годом позже вышла публикация, в которой описывался нечеткий PI-регулятор и его применения для управления парогенератором. С тех пор область применения нечетких регуляторов постоянно расширяется, увеличивается разнообразие их структур и выполняемых функций.
Нечеткая логика в PID-регуляторах используется преимущественно двумя путями: для построения самого регулятора и для организации подстройки коэффициентов PID -регулятора. Оба пути могут использоваться в PID -контроллере одновременно [2].

Рисунок 2 – Структура нечеткого PI –регулятора
Одна из наиболее распространенных структур нечеткого PI-регулятора) показана на рисунке 2. На вход регулятора поступает ошибка е и вычисляется ее производная по времени de/dt . Далее обе величины сначала подвергаются операции фаззификации (преобразования в нечеткие переменные), затем полученные нечеткие переменные используются в блоке нечеткого логического вывода для получения управляющего воздействия на объект, которое после выполнения операции дефаззификации (обратного преобразования нечетких переменных в четкие) поступает на выход регулятора в виде управляющего воздействия u.
Для применения методов нечеткой логики прежде всего необходимо преобразовать обычные четкие переменные в нечеткие. Процесс такого преобразования называется фаззификацией (от английского «fuzzy»- «нечеткий»). Он иллюстрируется рисунком 3. Диапазон изменения переменной e разбивается на множества (подмножества) NL, NM, NS, Z, PS, PM, PL, в пределах каждого из которых строится функция принадлежности переменной e каждому из множеств. На рисунке 2 функции принадлежности имеют треугольную (наиболее распространенную) форму, хотя в общем случае они могут быть любыми, исходя из смысла решаемой задачи Количество множеств также может быть произвольным.
Для нечетких множеств существует общепринятая система обозначений: N — отрицательный (Negative); Z — нулевой (Zero); P — положительный (Positive); к этим обозначениям добавляют буквы S (малый, Small), М (средний, Medium), L (большой, Large). Например, NL — отрицательный большой; NM — отрицательный средний (Negative Medium); PL — положительный большой. Количество таких переменных (термов) может быть любым, однако с увеличением их количества существенно возрастают требования к опыту эксперта, который должен сформулировать правила для всех комбинаций входных переменных.
Если величина ошибки e на входе нечеткого регулятора (рис. 2) равна e1 (рис.3), то соответствующее значение нечеткой переменной будет равно PS со степенью принадлежности подмножеству PS , равной μ(e1)=0,82 , или равно PM со степенью принадлежности μ(e1)=0,18. Степень принадлежности ошибки e1 другим множествам (Z, PL, NS и др.) равна нулю. Таким образом, величина ошибки e1 оказалась преобразованной в нечеткие переменные.
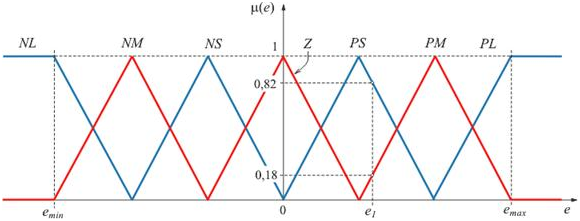
Рисунок. 2. Деление области изменения переменной e на множества NL, NM, NS и т.д. с функциями принадлежности μ(e) треугольной формы
Для выполнения функции регулирования над нечеткими переменными должны быть выполнены операции, построенные на основании высказываний оператора, сформулированных в виде нечетких правил. Совокупность нечетких правил и нечетких переменных используется для осуществления нечеткого логического вывода, результатом которого является управляющее воздействие на объект управления[3].
Список литературы:
- Аверкин А.Н., Батыршин И.З. и др. Нечеткие множества в моделях управления и искусственного интеллекта. М.: Наука. Гл. ред. физ-мат. лит., 1986. — 312 с.
- Батыршин И.З. Основные операции нечеткой логики и их обобщения. Казань: Отечество, 2001. — 100 с.
- Борисов В.В., Круглов В.В., Федулов А.С. Нечеткие модели и сети. М.: Горячая линия — Телеком, 2007. -284 с.[schema type=»book» name=»Нечеткая логика в PID -регуляторах» author=»Юрошева Татьяна Александровна, Козонова Марина Анатольевна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-30″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.04.2015_04(13)» ebook=»yes» ]

