Основой разработки сетецентрических информационных систем является методы и инструментарий информационной логистики, клиент-серверная и сервисно-ориентированная архитектуры, а также возможности глобальной сети, сетевых и Web-технологий.
Сетецентрическими называют системы, программное обеспечение (ПО), методы управления и прочие сферы, функционирующие в сетевой среде. Реализация распределенных многопользовательских информационных систем основывается на базе сетевой инфраструктуры, которая дает возможность интегрировать различные проблемно-ориентированные информационные системы, сервисы и информационные ресурсы, а также организацию общей точки доступа к ним различных групп пользователей, при этом, учитывая их полномочия и решаемые задачи информационной безопасности.
Одной из основных проблем качественного построения и стабильного функционирования информационных систем на всех стадиях их жизненного цикла является сбалансированность компонентов с учетом архитектурных, технологических решений и ресурсных характеристик сетевой и серверной среды, а также возможностей масштабирования. Решение задач данного типа, без развитых средств моделирования, затруднительно. Использование имитационного моделирования позволяет решать задачи анализа эффективности функционирования и синтеза сложных динамических систем [1- 3].
Математические модели являются основой для современных систем имитационного моделирования, из множества моделей широкое распространение получил аппарат сетей Петри [2–5]. Наличие различных классов сетей Петри позволяет осуществить на их основе моделирования сложных систем, представляя их в математическом (формализованном) виде, дающем возможность производить качественный анализ данных систем. Анализ сетей Петри и их реализация в виде компьютерной имитационной модели помогает получить важную информацию о структуре и динамическом поведении моделируемой системы и оценить возможные варианты организации системы с целью нахождения наиболее эффективных решений.
Рассматриваемый класс распределенных информационных систем и информационных сред реализуется на базе сетевых технологий и технологий Интернет в архитектуре «клиент-сервер».
Модель такой архитектуры описывает процессы функционирования и взаимодействия клиентской и серверной подсистем. В общем случае, моделируемая информационная среда содержит некоторое множество клиентов и «серверный кластер», при этом каждый клиент может обращаться с запросами к одному или более серверам, а каждый сервер серверного кластера взаимодействует с множеством клиентов и другими серверами.
Базовая модель в виде сети Петри
На текущий момент моделей, реализующих системы, подобного типа рассмотрены в [1, 2], но они не учитывают ряд особенностей межсетевого взаимодействия. Данное обстоятельство влияет на характеристики и качество модели.
Базовая модель сетецентрической информационной системы, реализованной на базе сетевых технологий и технологий Интернет в архитектуре «клиент-сервер», представлена в виде сети Петри на рис. 1.
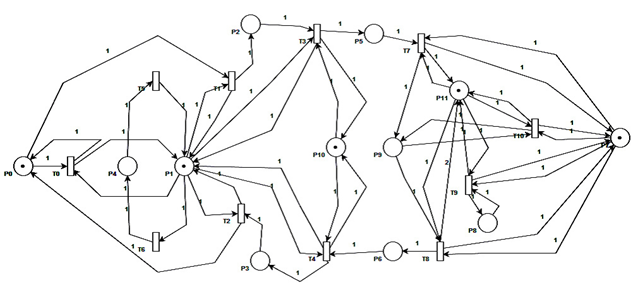
Рисунок 1. Взаимодействие компонентов сетецентрической
информационной системы
Спецификация позиций сети Петри для модели информационной системы в архитектуре клиент-сервер.
Зададим сеть Петри в виде:
![]() (1)
(1)
где P – множество позиций; T – множество переходов; I – входная функция; O – выходная функция; μ0 – начальная маркировка.
- конечное множество позиций: P={p0, p1, p2, p3, p4, p5, p6, p7, p8, p9, p10, p11}.
- конечное множество переходов: T={ t0, t1, t2, t3, t4, t5, t6, t7, t8, t9, t10}.
- множество входных позиций перехода:
I={I(t0), I(t1), I(t2), I(t3), I(t4), I(t5) ,I(t6), I(t7) ,I(t8), I(t9) ,I(t10) }.
I(t0)={p0, p1}, I(t1)= {p0, p1}, I(t2)={p1, p3}, I(t3)={p1, p2, p10}, I(t4)={p1, p6, p10}, I(t5)={p4}, I(t6)={p1}, I(t7)={p5, p7, p11}, I(t8)={p7, p9, p11}, I(t9)={p7, p8, p11}, I(t10)={ p7, p9, p11}.
- множество выходных позиций перехода:
O = {O(t0), O(t1), O(t2), O(t3), O(t4), O(t5), O(t6), O(t7), O(t8), O(t9), O(t10)}.
O(t0)={p0, p1}, O(t1)={p1, p2}, O(t2)={p0, p1}, O(t3)={p1, p5, p10}, O(t4)={ p1, p3, p10}, O(t5)={p1}, O(t6)={p4}, O(t7)={p7, p9, p11}, O(t8)={p6, p7, p11}, O(t9)={p7, p8, p11}, O(t10)={p7, p9, p11}.
- начальная маркировка:
μ0 = {1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1}
На основе приведенного описания состояний и переходов построена сеть Петри. Исходными данными для моделирования является начальная маркировка сети Петри. Формально, маркировка µ сети Петри -это функция, отображающая множество позиций P в множество неотрицательных чисел N [1-4]:
μ = P → n (2)
При начальной маркировке выполнены условия в позициях p0, p1, p7, p10 и p11, т.е. пользователь готов к началу сеанса, клиент и сервер находятся в режиме ожидания, а монитор безопасности готов открыть сессию для начала работы.
Полный анализ сети Петри проведем на основе рассмотрения ее динамических свойств, таких как достижимость, ограниченность, активность, обратимость, а также достижимость тупиковой разметки.
Таблица 1.
Спецификация элементов динамической модели
| Обозн.
элемента |
Описание |
Обозн.
элемента |
Описание |
| p0 | Информация о каждом приложения «клиента». Наличие поля ID в цвете маркера позволяет отличать данные различных клиентов при моделировании, а ids в поле Data – наборы данных. | t0 | Моделирует работу проблемной системы на стороне клиента, работа перехода определяется логикой «клиента». При срабатывании перехода происходит формирование набора записей Data, в зависимости от внешних условий или внутренних вычислений в переходе. |
| p1 | Информация о программном модуле «клиента», реализующий активный клиентский процесс. | t1 | Моделирует формирование запроса «клиента» к «серверу» |
| p2 | Информационные сообщения сформированные «клиентом» для передачи серверной подсистеме. (при передаче маркер несет в себе информацию о «клиента», инициировавшего передачу, в поле ID и при необходимости, устанавливается ненулевое значение ids в Data. | t2 | Моделирует процесс обработки «клиентом» сообщений, поступивших от «сервера» |
| p3 | Сообщения, поступающие «клиенту» от «сервера» | t3 | Реализует процесс передачи сообщений «клиента» серверной подсистеме |
| p4 | Программный модуль из библиотеки «клиента» | t4 | Реализует процесс передачи «клиентам» сообщений, сформированных «сервером» |
| p5 | Сообщения, поступившие от «клиентов» к «серверу» | t5 | Моделирует процесс смены состояния «клиента» из пассивного состояния в активное |
| p6 | Информационные сообщения, сформированные «сервером» для «клиентов» (маркер содержит непустое поле ID, определяющее получателя данного сообщения) | t6 | Моделирует процесс смены состояния «клиента» из активного состояния в пассивное |
| p7 | Программный модуль из библиотеки «серверной подсистемы», соответствующий активному процессу | t7 | Моделирует процесс приема сервером поступающих от «клиентов» сообщений и их первичной обработки |
| p8 | Программные модули из библиотеки «серверной подсистемы» | t8 | Выполнение процесса формирования «сервером» сообщений для «клиентов» |
| p9 | Информация о каждом серверном приложении | t9 | Моделирует работу внутрисистемных процессов серверной подсистемы по обработке запроса «клиента» с номером ID |
| p10 | Ресурсные возможности сетевой инфраструктуры для работы с клиентом с номером ID (например, пропускная способность канала) | t10 | Моделирует работу функциональной подсистемы проблемной системы, реализованной на серверном кластере |
| p11 | Спецификации вычислительных ресурсов серверного кластера (характеристика архитектуры и производительности кластера) |
В данной сети Петри все маркеры характеризуются цветом (ID, Data). При этом ID определяет идентификатор клиента (целое число), Data – непосредственно полный набор данных передаваемой информации между «клиентом» и «сервером» в парах:
– Data = list of (ids, key, value), где: ids – идентификатор набора данных в подсистеме клиента (целое число); key – название ключевого значения (строковый тип); value – значение поля (двоичный набор данных).
Время выполнения каждого перехода может быть определены фиксированными величинами, что фактически означает независимость продолжительности обработки запроса от сложности решаемой задачи, или рассматриваться в виде случайной величины. При этом наличие переходов t9 и t10 в модели позволяет учитывать загруженность сетевой инфраструктуры.
Достижимость. Маркировка μn достижима из маркировки μ0, если существует последовательность запусков, приводящих от μ0 к μn. Построенная сеть Петри является достижимой. Дерево достижимости представляет все достижимые маркировки сети Петри, а также – все возможные последовательности запусков её переходов [2,5-7]. Граф достижимости разметок представлен на рисунке 2.

Рисунок 2. Граф достижимости разметок динамической модели
сетецентрической информационной системы
Ограниченность. Сеть Петри называется k – ограниченной, или просто ограниченной, если для любой маркировки, достижимой от маркировки μ0, количество фишек в любой позиции не превышает некоторого числа k, то есть μ(р) ≤ К для любого р и любой маркировки μ, принадлежащей R(μ0). Представленная сеть не накапливает маркеров больше 3 в позициях p1 и p9
Активность. Сеть Петри активна (маркировка μ0 активна), если независимо от достигнутой μ0 маркировки, для любого перехода существует последовательность дальнейших запусков, приводящая к его запуску. Сеть является активной, т.к. ни один переход сети не является тупиковым.
Обратимость. Сеть Петри обратима, если для любой маркировки μ из R(μ0) маркировка μ0 достижима от μ. Построенная сеть не является обратимой, т.к. маркировка μ0 недостижима из любой маркировки μÎR(μ0). Достижимость тупиковой разметки делает дальнейшее срабатывание любого перехода в данной сети невозможным. Разработанная сеть Петри не имеет тупиковых разметок.
Построенная сеть Петри представляет собой модель информационного взаимодействия и имеет строгое математическое описание, позволяющее провести анализ взаимодействия трех субъектов информационных отношений: пользователя с клиентом и клиента с сервером.
В ходе исследования разработанной сети были выявлены основные статические и динамические свойства, на основании которых можно сделать вывод, что построенная сеть Петри является достижимой, ограниченной (со значением k = 3) и активной. При этом она является необратимой и имеет тупиковую разметку.
Выполнением сети Петри управляют количество и распределение фишек в сети. Переход запускается удалением фишек из его входных позиций и образованием новых фишек, помещаемых в его выходные позиции.
Переход запускается только в том случае, когда он разрешен. Запуск перехода в целом заменяет маркировку μ сети Петри на новую маркировку μ’, определяемую следующим соотношением:
![]() (3)
(3)
Запуски осуществляются до тех пор, пока существует хотя бы один разрешенный переход. Когда не останется ни одного разрешенного перехода, выполнение прекращается [4].
На основе предложенной сети Петри для моделирования сетецентрических многопользовательских информационных систем в программной инструментальной системе Pipe 3.0 разработаны компьютерные модели, которые позволяют анализировать проектные решения с учетом параметров информационной среды (характеристик информационной системы, состава и архитектуры серверного кластера, емкости используемых каналов передачи данных и т.д.). Такой анализ позволяет дать оценку масштабированных вариантов проектных решений сбалансированных относительно основных компонент рассматриваемой информационной системы.
Список литературы:
- Зыбарев Ю.М., Чернев С.П. Спецификация функциональной модели информационного портала сетями Петри. Эл. журнал Исследовано в России, 2003.
- Ломазова И. А. Вложенные сети Петри: моделирование и анализ распределенных систем с объектной структурой. М.: Научный Мир, 2004. 208 с.
- Зыбарев Е.Ю., Зыбарев Ю.М. Сети Петри как язык спецификации дискретных систем. Сборник трудов «Теория вычислений и языки спецификаций». – Новосибирск: изд-во ИМ СО РАН, 1995. – С. 186-201.
- Bernard P. Zeigler, Tag Gon Kim, Herbert, Theory of Modeling and Simulation. 2 edition, Academic Press, 2007.
- Jensen K. Coloured Petri Nets – Berlin a. o.: Springer- Verlag, 1996.
- Громов, Ю.Ю. Использование теории возможностей при оценке живучести сетевых информационных структур / Ю.Ю. Громов, А.А. Долгов, М.А. Хорохорин, Ю.В. Минин // Информация и безопасность. – Воронеж: Изд. ВГУ. – 2014. – № 1. Том 17. – С. 62-67. (65)
- Елисеев, А.И. Исследование структур сетевых информационных систем на основе толерантности в отношении достижимости вершин графа / А.И. Елисеев, Ю.Ф. Мартемьянов, В.Е. Подольский, В.Н. Шамкин // Приборы и системы. Управление, контроль, диагностика. – 2012. – №3 – С. 60-62. (101)[schema type=»book» name=»Моделирование взаимодействия клиента с сервером в информационной системе» description=»рассматриваются вопросы моделирования информационных систем, реализуемых в архитектуре «клиент-сервер», на основе сетей Петри. Построенная сеть Петри представляет собой модель информационного взаимодействия, обладающую строгим математическим описанием, которое позволяет проводить анализ взаимодействия между пользователем и клиентом, а также клиентом и сервером. Исследования динамической модели сетецентрической системы позволяют определить основные статические и динамические свойства, на основе которых можно сделать выводы о функционировании системы.» author=»Яковлев Алексей Вячеславович, Васюкова Екатерина Олеговна, Пеливан Михаил Анатольевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-26″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_31.10.15_10(19)» ebook=»yes» ]

