Экспериментальные данные, как правило, представляют собой изменение значения некоторого параметра во времени. При этом визуально выявить информативные признаки крайне сложно. В лучшем случае можно визуально оценить статистические характеристики процесса, дисперсию и математическое ожидание.
Если исследуемый процесс обладает, какой либо закономерностью или рядом закономерностей то последние будут тесно связаны с автокорреляционной составляющей процесса. Для того чтобы автокорреляционные составляющие процесса визуализировать предельно наглядно лучше всего представить исследуемый процесс в корреляционном поле. Таким образом, различные состояния технической или биологической системы, генерирующей исследуемый процесс, будут визуально отображаться в различные геометрические фигуры. Это может упростить диагностику.
В связи с ограниченными способностями исследователя к восприятию информации необходимо создать информационную модель. Информационная модель берет на себя роль устройства согласования ограниченных способностей исследователя с огромным потоком информации поступающей от исследуемого объекта. При этом согласование потока информации происходит путем подавления шумов и случайных флюктуаций, изменения масштаба, различного вида кодирования информационного потока данных и. т. д. [1]. В процессе этого модель избавляется от малозначительных избыточных данных. В результате получается изображение более точно и наглядно отображающее важнейшие свойства исследуемого процесса.
Для этих целей при обработке данных используется определенная совокупность моделей различного уровня [3].
ХМЭ М1М М2М …МnМ МФ,
Где Х – исследуемый объект;
М1М = Ф1 {МЭ} — математическая модель первого уровня;
МnМ — математическая модель n-го уровня;
МФ = Y { МnМ} — физическая модель;
МЭ = j {Х} — совокупность экспериментальных данных.
Преобразование j неизоморфно, а преобразования Ф1,Ф2,Ф3,…, Фn могут быть как изоморфными, так и неизоморфными [5]. Исследуемый процесс, как правило, представлен последовательностью цифровых отсчетов. Для выборки одного кадра достаточен размер векторов 10000 отсчетов. Для примера, из базы медицинских данных возьмем реализации векторов двух процессов ЭЭГ диагностически соответствующих двум группам пациентов, рисунок-1.
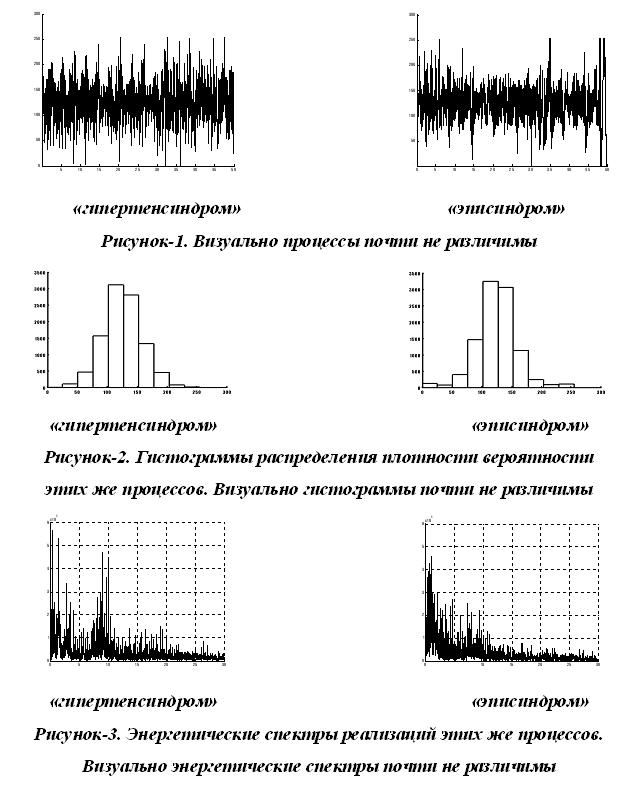
Очевидно, что для визуализации информативных признаков необходимо построить информационную модель. Поэтому для каждого вектора строится матрица измерений размером n x n. В нашем случае 100 х 100 отсчетов.
Человек способен визуально воспринимать объекты только в трех измерениях. Поэтому информационная модель должна включать в себя инструменты снижения размерности признакового пространства до трех измерений.
Но для сокращения размерности экспериментальных данных хотя бы одно из преобразований должно быть не изоморфным [3].
Именно с моделями сигналов, не изоморфными по отношению к входному сигналу, и связанно сокращение избыточности. Наглядным примером служит не изоморфный характер преобразований в процессах выделения информации из сигналов. Как уже отмечалось в [2,4], существует возможность отображения многомерной информации в пространстве низкой размерности.
Для реализации методов визуализации необходимо произвести отображение многомерной информации о исследуемых процессах в пространство, размерность которого не превышает р£ 3, т.е. размерности, которая доступна восприятию зрительным аппаратом человека.
Пусть Xi — i-мерный вектор описывающий объект исследования в i- мерной системе координат. Необходимо произвести ортонормированное преобразование системы координат с наименьшими потерями информативности.
В результате, исследуемый объект будет представлен новым p- мерным вектором Zp в новой p-мерной системе координат, причем p<<i, т.е. произвести сжатие статистической информации.
X — матрица реализаций вектора Xi размером n x n, где n = i0,5;
Σ — матрица ковариации размером n x n, вычисленная из матрицы X;
Z = ;
характеристическое уравнение матрицы Σ:

Ф — называется матрицей собственных векторов
Λ — называется матрицей собственных значений
Для описанных матриц имеют место следующие соотношения:
ФтФ = I (3)
ФтΣФ =Λ (4)
(Фт)т = Ф (5)
Ф-1=Фт (6)
Отсюда можно сделать следующие выводы:
- Можно найти такое линейное преобразование координат, что в новой системе координат ковариационная матрица будет иметь диагональный вид, и таким образом можно получить некоррелированные случайные величины, а в случае нормальных распределений — независимые случайные величины.
- Собственные значения инвариантны ко всем линейным невырожденным преобразованиям.
- Матрица такого линейного преобразования представляет собой транспонированную матрицу собственных векторов матрицы Σ. Так как собственные векторы есть векторы, максимизирующие d2(Z,0,Σ), то фактически в качестве новых координатных осей можно использовать главные компоненты распределения. Преобразование является ортонормированным и удовлетворяет (3), значит, при этом преобразовании сохраняется евклидово расстояние:
XтФФтX = XтX (7)
Реализация метода в программном пакете MATLAB достаточно проста, так как пакет имеет встроенные средства вычисления.
Кроме того пакет MATLAB имеет широкие возможности для визуализации полученных данных на экране монитора. С помощью MATLAB могут быть написаны, а затем реализованы на C++ программы для Windows предназначенные для практического применения. С помощью этих программ можно осуществлять мониторинг реальных процессов в сложных технических системах и приборах медицинской диагностики. Ниже приводятся примеры применения метода для визуализации экспериментальных процессов изображенных на рисунке 1 в двухмерном и трехмерном корреляционном поле главных компонент. Для каждого вектора строится матрица измерений размером n x n. Из матриц измерений вычисляются ковариационные матрицы размером n x n. В нашем примере используется размер матриц 100 х 100 отсчетов.
Используя встроенные средства MATLAB, вычисляются:
- pc – матрица образованная векторами, – главными компонентами;
- latent – вектор, элементами которого являются собственные числа;
- explained – вектор, элементами которого являются процентные доли общей дисперсии, объясняемые главными компонентами.

Далее строятся диаграммы рассеяния объектов в корреляционном поле главных компонент в пространстве образованном двумя первыми главными компонентами.
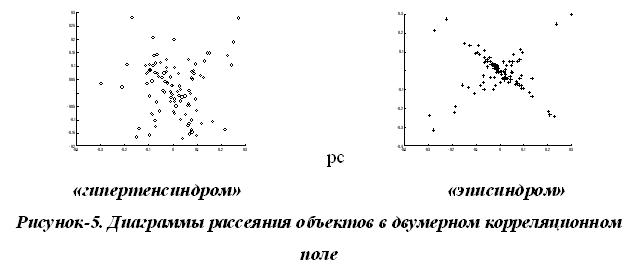
Информативные признаки, отличающие два экспериментальных процесса, уже четко визуально различимы и позволяют поставить диагноз. Аналогично строятся диаграммы рассеяния объектов в корреляционном поле главных компонент в пространстве образованном тремя первыми главными компонентами.
Информативные признаки, отличающие два экспериментальных процесса, также четко визуально различимы и позволяют поставить диагноз более точно, так как трехмерную геометрическую модель можно рассматривать с разных сторон.

Для визуального анализа данных по трехмерным диаграммам рассеяния, используются стереопары, которые можно вращать в пространстве средствами MATLAB для улучшения информативности. Показаны стереопары процессов на рисунке 1. Стереопары получаются путем поворота фигуры в горизонтальной плоскости на небольшой угол.
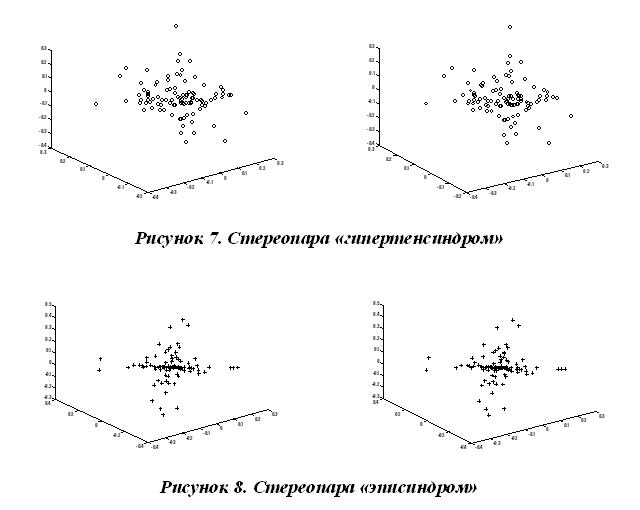
Информативные признаки, отличающие два экспериментальных процесса, также четко визуально различимы и позволяют поставить диагноз еще точнее, так как трехмерную геометрическую модель можно рассматривать, с разных сторон на экране 3D монитора. Для улучшения информативности визуализированное изображение можно вращать в пространстве и наблюдать в разных ракурсах. Представленный метод достаточно универсален и может применяться как для визуального представления данных одной выборки, так и в динамике в виде видео файла, состоящего из последовательности выборок, следующих с частотой кадров монитора или 3D телевизора используемого для вывода изображения.
Список литературы
- Александров В.В., Шеповальников А.Н., Шнейдеров B.C. Машинная графика электроэнцефалографических данных. — Л.: Наука, 1979, —152 с.
- Айвазян С.А., Бухштабер В.М., Енюков И.С, Мешалкин Л.Д. Прикладная статистика: Классификация и снижение размерности. — М.: Финансы и статистика, 1989, — 607 с.
- Галустов Г. Г. Теоретические и аппаратные основы, анализ и синтез сложных сигналов диагностических систем. // Диссертация на соискание ученой степени доктора технических наук — Таганрог. 1991 г.
- Галустов Г.Г., Мелешкин С.Н. Метод главных компонент в задачах снижения размерности признакового пространства биомедицинских данных с целью их визуализации // Материалы международной научной конференции «Цифровые методы и технологии», ч. 1.-Таганрог: Изд. «Антон», ТРТУ, 2005.- с. 34-37.
- Гастев Ю.А. Гомоморфизмы и модели: логико-алгебраические аспекты моделирования. — М.: Наука, 1975, — 150 с.
- Фуканага К. Введение в статистическую теорию распознавания образов: Пер. с англ. М.: Наука. 1979 г., 368 с.
- The design and analysis of pattern recognition experiments. — Bell SystemTech. J. 41, Chapter 5, p. 723-744[schema type=»book» name=»МЕТОД ВИЗУАЛИЗАЦИИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ В ТРЕХМЕРНОМ КОРРЕЛЯЦИОННОМ ПОЛЕ» author=»Мелешкин Сергей Николаевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-04-20″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 28.03.2015_03(12)» ebook=»yes» ]

