Одной из важнейших задач развития научных основ конструирования и технологии изготовления изделий различного назначения является создание адекватных математических моделей, описывающих поведение и состояние конструкций и их отдельных элементов в процессе их производства,испытаний, транспортировки, хранения и эксплуатации.
Нарастающая сложность конструкций изделий различного назначения приводит к серьезным экономическим потерям в производстве и эксплуатации. Анализ отказов изделий и их составных частей позволяет утверждать ,что одной из основных причин снижения их надежности, полных или частичных отказов являются процессы , происходящие в соединениях разнородных материалов под действием внешних и внутренних дестабилизирующих факторов . При этом основными являются статические, динамические и тепловые воздействия,возникающие на всех стадиях жизненного цикла изделия: технологические операции в производстве,испытания , хранение, транспортировка и эксплуатация [1,с.10; 2,с.8].
Анализ конструктивных особенностей современных изделий приборостроения и их составных частей показывает,что большинство из них предоставляет собой гетерогенные структуры ,сочетающие в себе материалы с различными физико-механическими свойствами , обеспечивающими требуемую надежность и безопасность изделия в заданных режимах эксплуатации [3,с. 3].
Для исследования процессов ,происходящих в структурах этих изделий под действием внешних факторов, необходима разработка математических моделей и комплексов проблемно-ориентированных программ для проведения вычислительных экспериментов, позволяющих адекватно описывать процессы и напряженно — деформированное состояние (НДС) на всех этапах их жизненного цикла [4,с. 147].
Рассмотрим это на примере микросборок прямоугольного типа, имеющих широкое практическое применение в приборостроении и изделиях радиоэлектроники . На одной или нескольких гранях внутри микросборки размещаются платы с резистивными элементами, обеспечивающие требуемые выходные параметры микросборки . Эти микросборки представляют собой многослойные гетерогенные системы, которые в процессе их изготовления и эксплуатации подвергаются тепловым и механическим воздействиям .Для проверки герметичности при изготовлении они подвергаются технологической опрессовке внешним избыточным давлением, под действием которого происходит деформация граней корпуса и плат с резистивными элементами, что вызывает изменение их выходных электропараметров.
Для анализа НДС таких микросборок и их элементов предложены различные модели, позволяющие моделировать их состояние при технологический опрессовке корпусов и научно-обоснованно определять предельно допустимое давленние с учетом их конструктивных особенностй [5,с.102;6,с.87;7,с.191]. Аналогичные исследования проведены и при тепловых технологических и эксплуатационных воздействиях на микросборки [4,с.146]. Вопросы моделирования и исследования динамических процессов, происходящих в микросборках при вибрационном воздействии а настоящее время исследованы недостаточно.
Рассмотрим внешнее динамическое воздействие на микросборку .Типовая конструкция микросборки прямоугольного типа показана на рис.1. Микросборка крепится к изделию винтами в четырех точках и имеет габаритные размеры корпуса по осям x,y,z соответственно a×b×H,где a×b— размеры в плане; H-высота корпуса микросборки.На основании корпуса (рис.1б) расположена плата,имеющая толщину h и размеры в плане aп×bп. Плата крепится к основанию паяным или клеевым швом толщиной hш. Материал платы характеризуется модулем Eп и коэффициентом Пуссона νп ,а материал шва модулем сдвига Gш и коэффициентом Пуссона νш .
В общем случае считается, что грани корпуса микросборки изготовлены из различных материалов, механические свойства которых характеризуются модулями упругости Еj и имеют толщины hj, где j = 1,2 ,…, 6 – номер грани. Для определённости будем считать, что j = 6 соответствует крышке корпуса, j = 1 – основанию с платой, j = 2…5 – боковым стенкам корпуса.
Считается , что на плату со стороны корпуса изделия в направлении z действует гармоническая вибрация, при которой в процессе эксплуатации возможны резонансные явления, возникающие в элементах микросборки (крышка,боковые стенки , основание , плата,шов).
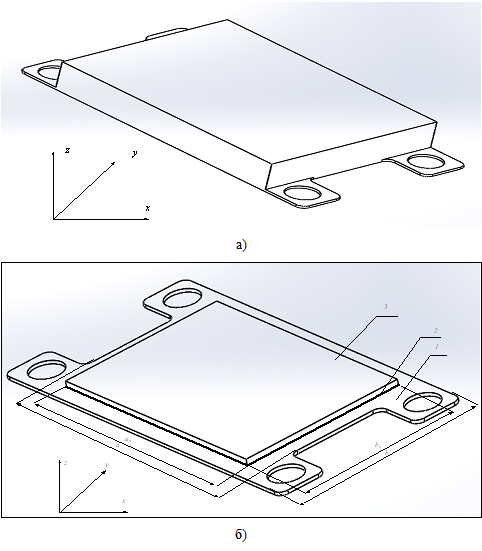
Рисунок 1.Конструкция микросборки;а-обший вид;б-основание с платой:
1-основание, 2-шов, 3-плата
В качестве адекватной молели, позволяющей исследовать динамические процессы в элементах микросборки, используется пространственная модель микросборки в виде гетерогенной структуры с использованием метода конечных элементов, реализованного в программном комплексе ANSYS аналогично [7,с.88].Такая модель позволяет учитывать взаимное влияние граней корпуса, реальные размеры плат и их места расположения на гранях ,а также влияние физико-механических характеристик применяемых материалов плат ,шва и граней корпуса . Кроме этого модель позволяет учитывать наличие внутри корпуса нескольких многослойных плат, в том числе расположенных на разных гранях корпуса, что может приводить к отсутствию симметрии в конструкции микросборки и усложнению ее НДС. Предложенная модель является пространственной и наиболее общей по сравнению с расчетными моделями, представленными в [2,с.148;6,с.192].
На основании предложенной модели были исследованы динамические характеристики различных типоразмеров микросборок рассматриваной конструкции . Установлено, что формы колебаний микросборок, их собственные частоты и места расположения наиболее нагруженных зон их элементов, где возможно возникновение и развитие дефектов, существенно зависит от массогабаритных размеров микросборок и особенностей их конструктивного исполнения.
В качестве примера приведем некоторые результаты численного моделирования динамических характеристик для микросборки, имеющей следующие размеры: a× b× H=(36×24×5) мм . Плата расположена в центре основания и крепится к нему клеем ВК -9 .Корпус изготовлен из сплава 29НК (Еj=1,4.105 МПа , νj=0,3 при j=1,2,. ..,6) ; плата –из ситалла (Еп=9,693.105 МПа , νп=0,25),а свойства шва характеризуется модулем сдвига Gш=1000МПа. Толщины элементов микросборки приняты следующими: hj=0,4мм(при j=1,2,..,6);h =0,6мм;hш=0,1мм. Рассмотрены два варианта микросборки:
-I вариант: плата имеет размеры aп×bп =(30×20) мм;
-II вариант: плата имеет размеры aп×bп =(15×10) мм.
В таблица для рассматриваемых микросборк приведены значения первых десяти резонансных частот и указаны наиболее нагруженные резонирующие элементы микросборки ,соответствующие каждой частоте.
Таблица 1.
Собственные частоты fj и резонирующие элементы микросборки
| Номер частоты j |
Микросборка I |
Микросборка II |
||
| fj (Гц) | Элемент | f j(Гц) | Элемент | |
| 1 | 3252 | крышка | 3210 | крышка |
| 2 | 5234 | крышка | 4028 | крышка и основание с платой |
| 3 | 5671 | основание с платой | 5181 | крышка и основание с платой |
| 4 | 7362 | крышка | 6286 | крышка и основание с платой |
| 5 | 8478 | крышка | 7301 | крышка и основание с платой |
| 6 | 10010 | крышка | 8454 | крышка |
| 7 | 10125 | основание с платой | 8769 | крышка и основание с платой |
| 8* | 10938 | крышка и основание с платой | 9953 | крышка |
| 9 | 12852 | крышка и основание с платой | 11944 | основание с платой |
| 10 | 12910 | крышка | 12339 | крышка и основание с платой |
Анализ анимационной картины деформаций элементов конструкций микросборок показал :
— резонансов боковых стенок микросборок в рассматриваемом диапазоне частот не наблюдается;
-спектр резонансных частот элементов микросборки является достаточно плотным;
— основными резонирующими элементами являются крышка и основание с платой;
— основными формами колебаний крышка и основание с платой являются их изгибные колебания по оси z;
— на частотах, отмеченных звездочкой (*), наблюдаются изгибно- крутильные колебания всей микросборки относительно оси x: для микросборки I f* =f8= 10938 Гц, а для микросборки II изгибно- крутильные колебания имеют место на более высокой частоте f* =f14 = 14967 Гц;
— значения резонансных частот элементов микросборки и соответствующие им формы колебаний наиболее нагруженых элементов существенно зависит от размеров платы, установленной на основании. При увеличении размеров платы величины резонансных частот уменьшаются,т.к. приведенная жесткость основания с платой уменьшается;
— наиболее опасными являются резонансные явления, возникающие в основание с платой,т.к. в этом случае возможно возникновение и развитие дефектов в виде микротрещин в клеевых (или паяных)швах,а также ухудшение метрологических характеристик микросборки из -за повышенной деформации резистивных элементов, расположенных на поверхности платы;
— собственные частоты и соответсвующие им формы колебаний зависят от способа крепления микросборки к ответной части изделия.
На рис.2 для микросборки II показаны первые пять форм колебаний,характеризующиеся вертикальными прогибами в направлении оси z (рис.1).Боковые стенки корпуса на рис.2 условно не показаны.
Анализ НДС элементов микросборки на резонансных частотах проводился по эквивалентным напряжениям,которые определялись по критерию Мизеса при действующем ускорении,равном 10 g , где g -ускорение свободного падения. Флажками на рис.2 показаны точки элементов микросборки, в которых достигаются максимальные эквивалентные напряжения (max σ) при резонансе на различных формах колебаний.
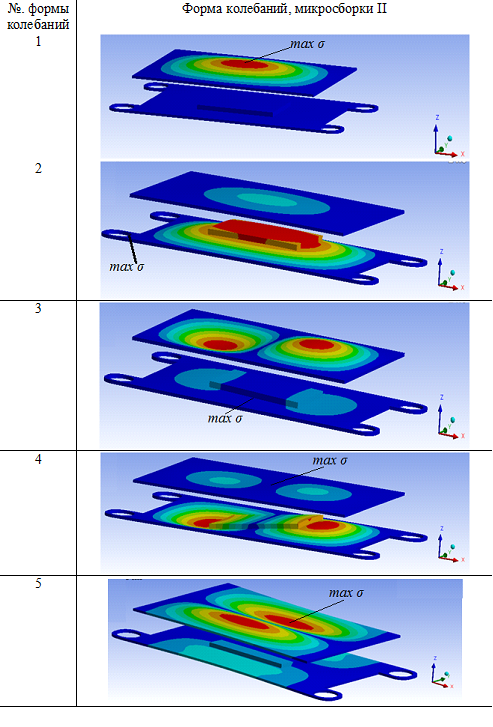 Рисунок 2.Формы колебаний для микросборки II
Рисунок 2.Формы колебаний для микросборки II
Численное моделирование НДС,проведенное для различных типоразмеров микросборок,показало:
— наиболее нагруженными элементами микросборки в зависимости от внешнего частотного воздействия являются крышка, основание, плата и шов, соединяющий плату с основанием ;
— НДС существенно зависит от геометрических размеров корпуса и платы , а также частоты внешнего воздействия ;
— положение наиболее нагруженной точки конструкции существенным образом определяется формой колебаний , реализуемой в элементах конструкции при динамическом воздействии.
С точки зрения обеспечения надежности микросборки при эксплуатационных динамических воздействиях наибольший интерес предоставляет анализ НДС платы,шва и основания микросборки. Это анализ позволяет определить зоны возможного образования латентных дефектов уже на ранних этапах конструкторский разработки микросборок и принять соответствующие конструкторско-технологические решения, обеспечивающие вибропрочность конструктивных элементов и микросборки в целом.
Обобщая проведенный анализ ,укажем на то,что разработка и применение математических моделей и программно — ориентированных вычислительных комплексов, позволяет на ранних этапах конструирования и разработки технологических процессов изготовления обеспечивать требуемую надежность и виброустойчивость проектируемых конструкций . Выбор расчетной математической модели и её уровня сложности (одномерная,двумерная, трехмерная, учет гетерогенности и других конструктивных особенностей) определяется свойствами и требуемой точностью анализа НДС проектируемой конструкции.
Список литературы
- Литвинов, А. Н., Литвинов М.А., Смогунов В.В. Прикладные модели механики гетерогенных структур изделий приборостроения: монография.-Пенза: Изд-во пенз.гос.ун-та. — 2009.-320с.
- Литвинов, А. Н. Моделирование динамических процессов в изделиях приборостроения: монография .- Пенза : Изд-во ПГУ, 2011. — 196 с.
- Хади,О. Ш., Литвинов А.Н. Моделирование напряженно-деформированного состояния корпусов микросборок в процессе их изготовления и эксплуатации. Динамика и прочность(глава 1). Избранные труды всеросс.научн. конф. по проблемам науки и технологий. –М.:РАН,2013.-С.3- 26.
- Литвинов А.Н., Хади О. Ш. , Юрков Н.К. Моделирование напряженно-деформированного состояния слоистых структур РЭС при технологических и эксплуатационных воздействиях. Известия вузов. Поволжский регион .Технические науки :Изд-во ПГУ,2014.-№4.- С.146-157.
- Hadi A. Sh., Litvinov A.N. Study of layer structures in the devices of instrument engineering for increasing safety in the process of their operational lifetime, ISJ theoretical & applied Science . 2015.-N 04 (24),-p.101-107.
- Литвинов А.Н., Хади О. Ш. Оценка точности приближенного метода определения допустимого давления для корпусов микросборок. Актуальные проблемы современного машиностроения : сборник трудов Междунар.научно-практ. конф. Юрга: Изд-во Юрг. гос.ун-та,2014.-С.191-194.
- Хади,О. Ш., Литвинов А.Н. Исследование НДС микросборок при технологической опрессовке в программном комплексе ANSYS. Инженерные исследования и достижения-основа инновационного развития: Материалы IV Всеросс. научно- практ. конф. Рубцовск : Изд-во Рубцовский индустриальный институт,2014.-С.87-94[schema type=»book» name=»ДИНАМИКА МИКРОСБОРОК ПРЯМОУГОЛЬНОГО ТИПА» description=»Рассматриваются микросборки замкнутого типа,имеющие прямоугольную форму и подверженные динамическому нагружению. Выполнено математическое моделирование форм собственных колебаний и определены собственные частоты колебаний элементов микросборок,имеющих различные типоразмеры .Дан анализ динамической виброустойчивости микросборок.» author=»Хади Одей Шакер, Литвинов Александр Николаевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-28″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.04.2015_04(13)» ebook=»yes» ]

