Под понятием туннелирование или нарушенное полное внутреннее отражение (НПВО) понимается способность квантовых частиц проникать сквозь потенциальные барьеры, высота которых превышает кинетическую энергию частиц, и преодолевать тем самым абсолютно запрещенную для них по законам классической механики подбарьерную область. [1].
Особый интерес к эффектам туннелирования возник с появлением метаматериалов, электромагнитные или механические параметры которых непрерывно распределены внутри среды по заданному закону, контролируемому технологией изготовления.
Такие материалы привлекли внимание благодаря возможности их применения для контроля над электромагнитным излучением на субволновых расстояниях. Ряд таких задач решается в оптике с использованием тонких диэлектрических плёнок, показатель преломления которых изменяется в направлении поперек пленки (так называемые градиентные фотонные барьеры). Особое внимание уделяется при этом процессам отражения и пропускания волн тонкими слоями неоднородных материалов, размеры слоев и масштабы неоднородности которых соизмеримы с длиной волны.
Проблемы распространения волн в средах с непрерывным пространственным изменением показателя преломления составляют обширную область математической физики – оптике градиентных сред. Выбирая направление изменение градиента за ось z, можно представить их диэлектрическую проницаемость в виде
![]()
Здесь n0 –значение показателя преломления на границе среды z=0; U – некоторая безразмерная, дважды дифференцируемая функция, определяющая пространственный профиль показателя преломления. Рассматривая распространение электромагнитной волны, падающей из вакуума нормально к границе z= 0 в направлении z, можно выразить компоненты волнового поля Ex и Hy через вспомогательную функциюΨ:
![]()
Функция Ψ определяется волновым уравнением, следующим из уравнений Максвелла:
![]()
Отражение и пропускание электромагнитных волн градиентным диэлектрическим барьером конечной толщины зависит от нелокальной дисперсии, определяемой формой профиля U(z) и шириной барьера d. Чтобы представить такую зависимость в явной форме, нужно использовать гибкую модель U(z), допускающую точное решение уравнения (3) без каких-либо допущений о малости или медленности изменений полей и параметров среды. В электродинамике слоистых сред известны точно решаемые модели, описывающие монотонную зависимость U2(z) от одного параметра – характерной длины L:
Используем модель U2 с двумя свободными параметрами L1 и L2, представляющая вогнутый профиль показателя преломления (рис. 1):

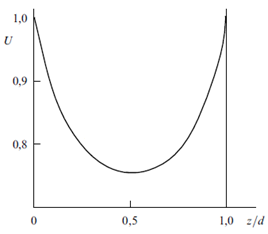
Рисунок 1. Нормированный профиль показателя преломления (4), U(z)
Безразмерная величина Q, определяемая из условий непрерывности полей на задней границе барьера z = d представляет вклад обратной волны в поле внутри барьера, переменная η – фазовая длина пути:

Зависимость волнового числа от частоты (дисперсия) описывается формулой волноводного типа, при этом величина Ω (10) играет роль частоты отсечки. Следует подчеркнуть, что появление критической частоты в неоднородном барьере определяется не свойствами материала барьера, а геометрическими параметрами – формой профиля U(z) и шириной барьера d. Когда эффекты неоднородности ослабевают (L1, L2→∞), эта нелокальная дисперсия уменьшается, частота отсечки надает до нуля и формула для волнового числа (10) принимает вид q = kn0.
Нелокальная дисперсия барьера отделяет область высоких частот (u<1, U2> 0), соответствующую режиму распространения, от низкочастотной области (u>1, U2< 0), связанной с режимом туннелирования. Этот режим рассматривается ниже в процессе решения волнового уравнения (6); причем функцию Ψt для туннелирующего поля можно получить из (6), делая там замену q→ip, N→iN_, N_ = :
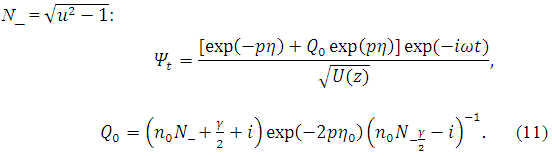
Величина Q0 получается из Q (7) при этой же замене.
Подставив (11) в (2), найдем компоненты ноля Ех и Ну внутри барьера в режиме НПВО. Условия непрерывности этих компонент на границах барьера дают явные выражения для коэффициента отражения R и функции пропускания Т.
Данное решение описывает простой случай НПВО в единичном фотонном барьере. Для оптимизации таких эффектов рассмотрим туннелирование через систему m смежных одинаковых слоев. Используя условия непрерывности полей на границах между смежными слоями, можно найти поле в каждом слое; присвоив номер m = 1 слою на дальней стороне системы, получим рекуррентную формулу для параметра Qm, соответствующего m-му слою(m≥ 1):


![]()
При этом сдвиг фазы туннелирующей волны не накапливается в процессе распространения, а формируется на границе. С увеличением числа барьеров (m≥ 1, tm→ 1) модуль функции пропускания уменьшается по закону ехр (–2mpη0), а фаза, как видно из (16), при tm→ 1 стремится к постоянному значению ϕm, не зависящему от числа барьеров (рис. 2, кривая 1). При этом «Фазовое время» τ также стремится с ростом m к постоянному значению (рис. 2, кривая 2). При этом в системе неоднородных фотонных барьеров возникает парадокс Хартмана: скорость туннелирования v = md/τ должна повышаться с ростом ширины барьера md, достигая при m = 10 значения v = c; дальнейший рост привел бы к сверхсветовым значениям (v>c). Более того, вблизи частоты отсечки возможно появление «отрицательного времени» туннелирования τ< 0.
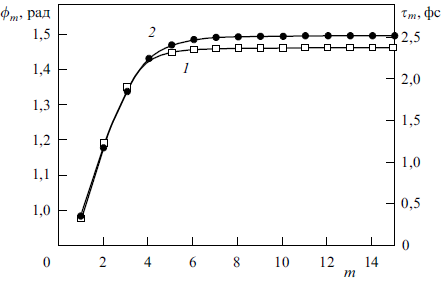
Рисунок 2. Зависимость фазы ϕm (кривая 1) и фазового времени τm (кривая 2) волны, туннелирующей через систему градиентных слоёв (4) U(z), от числа слоёв.
Таким образом, расчет времени туннелирования по формуле (9) приводит к возникновению в теории НПВО сверхсветовых скоростей и отрицательных времён. Однако эти проблемы не возникают, если связывать время туннелирования с групповой скоростью волны в барьере vg. Определив vg через поток энергии Р и плотность энергии W(z) и найдя Р и W(z) для туннелирующего поля (10), видно, что внутри барьера vg(z) = P/W(z) < с. Значения vg(z) для неоднородного барьера удобно сравнить со скоростью переноса энергии в поле, сформированном внутри однородного слоя диэлектрика с показателем преломления n0 при интерференции прямой и обратной волн. Эта скорость vg0, зависит от n0 и не зависит от z:
![]()
Для простоты анализа выше рассматривался режим НПВО в градиентном слое без подложки. При учете влияния подложки эффекты нелокальной дисперсии остаются в силе, хотя зависимость от параметров подложки приводит к усложнению формул. Так, граничные условия на поверхности однородной подложки, толщина которой значительно больше длины туннелирующего импульса, а показатель преломления равен w, приводят вместо (11) к другому выражению, описывающему вклад обратной волны:
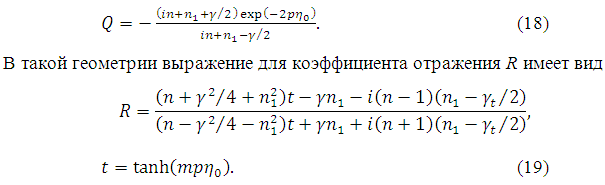
При n = 1 формула (19) переходит в (14).
Как видно из (19), система из нескольких градиентных пленок может быть эффективным отражателем.
Заключение
Использование эффектов туннелирования волн весьма перспективно как в прикладных задачах градиентной нанооптики (тонкослойные фильтры и поляризаторы, рефлекторы и безотражательные покрытия), так и при решении принципиальных вопросов, связанных с оптимизацией процессов переноса энергии волнами различных спектральных диапазонов. Другое важное направление формируется при обобщении оптических эффектов НПВО на нелокальные квантово-механические процессы туннелирования электронов через потенциальные барьеры. Общность концепций НПВО для различных волновых полей начинает привлекать внимание и при анализе динамики частиц в атомной физике.
Исследование выполнено при поддержке ДВФУ, проект № 14-08-2/3-20_и
Список литературы:
- Гольданский В. И.Туннельные явления в химической физике / В.И. Гольданский, Л.И.Трахтенберг, В.Н.Флёров // М.: Наука, 1986. — 296 с
- Шварцбург А.Б.Парадоксы нанооптики метаматериалов / А.Б. Шварцбург// В мире науки.-2014,- № 10.- С. 37-45.
- Шварцбург А.Б. Резонансное туннелирование сверхкоротких электромагнитный импульсов в градиентных метаматериалах: парадоксы и перспективы / А.Б. Шварцбург, Н.С. Ерохин // УФН 181. – 2011, — №11. – С. 1212-1217.
- Шварцбург А.Б. Нанооптика градиентных электрических плёнок / А.Б. Шварцбург, М.Б. Агранат, О.В. Чефонов // «Квантовая электроника». – 2009, — №10. – С. 948-952.
- Шварцбург А.Б. Туннелирование электромагнитных волн – парадоксы и перспективы / А.Б. Шварцбург // УФН 177. – 2007, — №1. – С. 43-58.[schema type=»book» name=»БЕЗОТРАЖАТЕЛЬНОЕ ТУННЕЛИРОВАНИЕ СВЕТА ЧЕРЕЗ ГРАДИЕНТНЫЕ ФОТОННЫЕ БАРЬЕРЫ» description=»Рассмотрены процессы туннелирования света через одиночные и многослойные градиентныефотонные барьеры. Показана зависимость от нелокальной дисперсии отражения и пропускания электромагнитных волн градиентным диэлектрическим барьером.» author=»Туркин Дмитрий Геннадиевич, Волокитин Егор Игоревич, Шевель Владислав Валерьевич, Силина Наталья Николаевна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-26″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_31.10.15_10(19)» ebook=»yes» ]

