В настоящее время использование волоконно-оптических датчиков (ВОД), в различных сферах деятельности человека чрезвычайно высоки. Рассмотрим основные особенности и преспективы их использования: При анализе взаимодействия симметричного четырехчастотного излучения выберем некоторый контур, отражающий нормированную зависимость поглощения от частоты.
Рассмотрим особенности взаимодействия четырехчастотного колебания с контуром при дифференциальном анализе.
Будем считать, что амплитуды составляющих входного колебания, равны А1вх = А2вх = А3вх = А4вх = 1. Частоты составляющих попарно симметричны относительно несущих частот ∆ɛ1 и ∆ɛ2каждого из каналов, которые в свою очередь симметричны относительно средней обобщенной расстройки четырехчастотного входного колебания ∆ɛ0и равны:
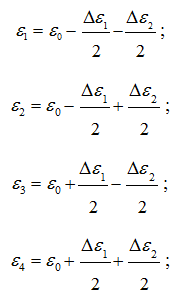
где Δε1- расстройка между несущими,
Δε2-расстройка между частотами составляющих четырехчастотного сигнала относительно несущих частот.
Спектр сигнала представлен на рисунке 1:
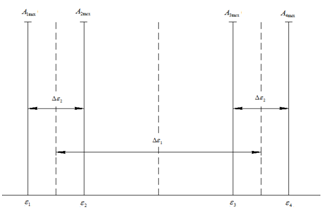
Рис 1 — Спектр четырехчастотного сигнала на входе контура.
Обобщенная амплитудно-частотная характеристика Гауссового контура, на вход которого подается четырехчастотный сигнал, можно определить с помощью следующего выражения и представленная на рисунке 2:
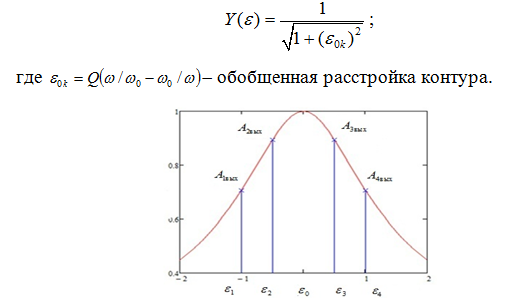
Рис 2 — АЧХ Гаусcова контура со спектром выходного
четырехчастотного сигнала
Из рисунка 2 видно, что значения амплитуд составляющих выходного четырехчастотного сигнала А1вых , А2вых , А3вых , А4выхзависят от значений АЧХ контура на соответствующих значениях обобщенной расстройки составляющих входного четырехчастотного сигнала ε1, ε2, ε3, ε4, причем А1вых=А1вхY1 ,А2вых=А2вхY2, А3вых=А3вхY3 , А4вых=А4вхY4 .Определим уравнение контура по Гауссу, зависимостей амплитуд составляющих выходного четырехчастотного сигнала от обобщенной расстройки:
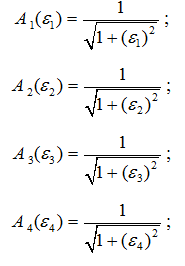
Производя математические преобразования получим:
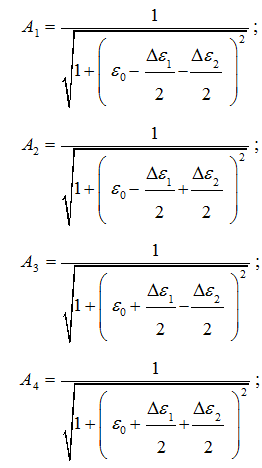
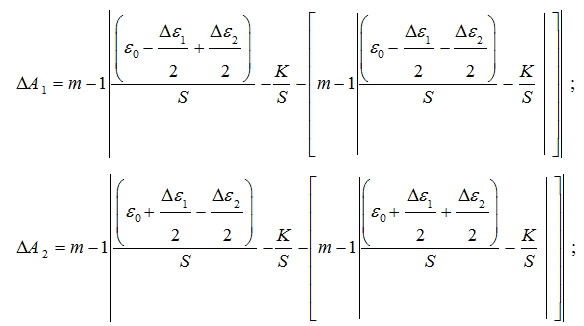
Следовательно, разности амплитуд между составляющими выходного четырехчастотного сигнала, ∆Авых , определяются выражениями вида:
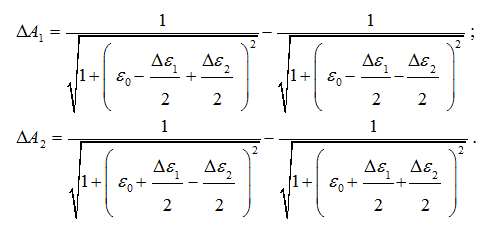
Рассмотрим амплитудно-частотную характеристику, выходную амплитуду и разность амплитуд сигнала, для треугольного контура, на вход которого подается четырехчастотный сигнал, определим эти значения с помощью следующего выражения и представленная на рисунке 3:
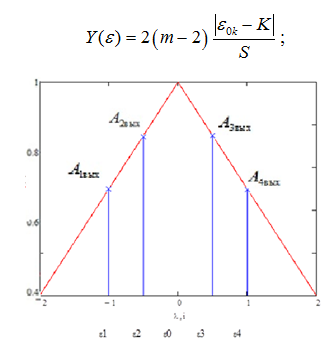
Рис 3 — АЧХ треугольного контура со спектром
выходного четырехчастотного сигнала
Запишем уравнения, треугольного контура, зависимостей амплитуд составляющих выходного четырехчастотного сигнала от обобщенной расстройки:
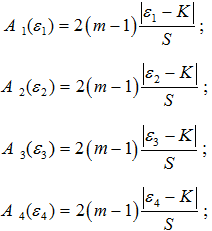
Разности амплитуд между составляющими выходного четырехчастотного сигнала, определяются выражениями вида:
Рассмотрим амплитудно-частотную характеристику, выходную амплитуду и разность амплитуд сигнала, для вогнутого контура, на вход которого подается четырехчастотный сигнал, можно определить с помощью следующего выражения и представленная на рисунке 4:
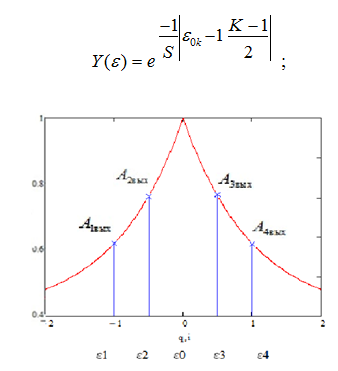
Рис. 4- АЧХ вогнутого контура со спектром
выходного четырехчастотного сигнала
Уравнения, вогнутого контура, зависимостей амплитуд составляющих выходного четырехчастотного сигнала от обобщенной расстройки представлена видом:
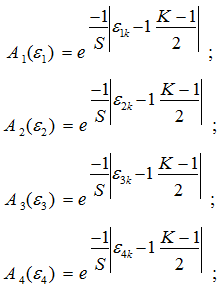
Разности амплитуд между составляющими выходного четырехчастотного сигнала определяются выражениями вида:
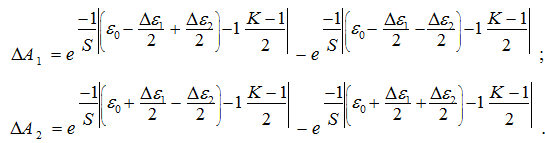
Анализируя полученные выражения следует, что разности амплитуд составляющих четырехчастотного сигнала зависят от средней обобщенной расстройки (ε0), расстройки несущих частот (∆ε1) и от разностных частот между составляющими четырехчастотного сигнала (∆ε2) .
Рассмотрим зависимость разности амплитуд составляющих выходного четырехчастотного сигнала от значения средней обобщенной расстройки четырехчастотного сигнала ∆Авых(ε0) при разных значениях расстройки между частотами ∆ε2.Результаты расчетов зависимости ∆Авых(ε0)для разных значений ∆ε2представлены на рис. 5 – 7 :
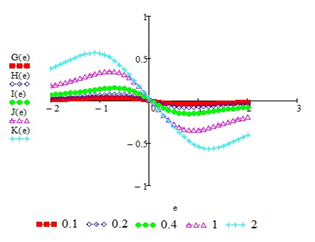
Рис 5 — Зависимость ∆Авых(ε0) для разных значений
∆ε2 для Гауcсово контура

Рис 6 — Зависимость ∆Авых(ε0) для разных значений
∆ε2 для треугольного контура
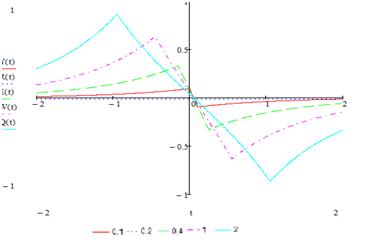
Рис. 7 — Зависимость ∆Авых(ε0) для разных значений
∆ε2 для вогнутого контура
Из рисунков 5 и 6 видно, что графики зависимости ∆Авых(ε0) — кривые 3-го порядка, проходят через нуль при Δε0=0 и Δε1=0. Функция ∆Авых(ε0)непрерывна, возрастает до максимума, убывает до минимума и снова возрастает. Но на рисунке6 значения разности амплитуд составляющих выходного четырехчастотного сигнала от значения средней обобщенной расстройки сигнала ∆Авых(ε0), принимаю больше значения чем на рисунке 5.
При исследовании воздействия четырехчастотного сигнала на контуры, показано, что максимальная чувствительность к изменению средней частоты четырехчастотного сигнала достигается при значении расстройки между составляющими сигнала равной полосе пропускания исследуемого контура.
Работая с четырехчастотным сигналом достаточно сравнения амплитуд гармонических составляющих сигнала для реализации метода точного определения частоты контура.
Список литературы:
- Дураев, В.П. Перестраиваемые одночастотные полупроводниковые лазеры/В.П.Дураев // Физика и техника полупроводников, 2014, том 48, вып. 1
- Садеев, Т.С. Фотонные фильтры микроволновых на основе одночастотного лазера и амплитудного электрооптического модулятора Маха-Цендера: дис. к.т.н/Т.С.Садеев Казань 2011
- Гаврилов, А.М. Нелинейная дисперсия трехчастотного волнового пакета в бездисперсионной квадратично-нелинейной среде. Эксперимент/Гаврилов, А.М. // Электронный журнал «Техническая акустика» 2005, 29
- МПК G01K 11/32 (2006/01). Устройство для измерения параметров физических полей / Денисенко П.Е, Куприянов В.Г., Морозов О.Г., Морозов Г.А., Садеев Т.С., Салихов А.М. (КНИТУ им. А.Н. Туполева). №2012124693/28(037831); Заявл. 14.06.2012
- Морозов, О.Г. Симметричная двухчастотная рефлектометрия в лазерных системах контроля параметров природной и искусственных сред: дис. д.т.н./Морозов О.Г. Казань 2004
- Ming Li, Junya Hayashi, and Hongpu Li. Advanced design of a complex fiber Bragg gratingfor a multichannel asymmetrical triangular filter- J. Opt. Soc. Am. B / Vol. 26, No. 2 / February 2009.[schema type=»book» name=»АНАЛИЗ ВЗАИМОДЕЙСТВИЯ ЧЕТЫРЕХЧАСТОТНОГО КОЛЕБАНИЯ С ГАУССОВЫМ, ТРЕУГОЛЬНЫМ И ВОГНУТЫМ КОНТУРОМ ПОГЛОЩЕНИЯ» description=»В данном докладе рассмотрен принцип работы оптоволоконной решётки Брегга, проведен анализ взаимодействия четырехчастотного колебания с Гауссовым, треугольным и вогнутым контуром поглощениявыявлены основные особенности и недостатки.» author=»Малых Дмитрий Вячеславович, Файзуллин Ренат Илдусович, Галин Артем Викторович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-21″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_25.07.15_07(16)» ebook=»yes» ]

