Введение
Измерение несущей частоты радиосигналов является одной из важнейших задач различных систем обнаружения и анализа параметров радиосигналов, в частности систем радиомониторинга. Переход к цифровой обработке сигналов в таких системах требует разработки цифровых приемников и алгоритмов обработки радиосигналов. Важным параметром приемников систем радиомониторинга при решении задачи измерения несущей частоты радиосигнала является полоса частот, в которой осуществляется анализ сигналов. Традиционный подход к расширению рабочей полосы частот цифрового приемника заключается в повышении частоты дискретизации аналого-цифрового преобразователя (АЦП). При этом полоса частот ∆F обрабатываемого радиосигнала и частота дискретизации fs связаны теоремой Найквиста-Котельникова о низкочастотной дискретизации:
fs ≥ 2∆F (1)
Однако в этом случае возрастают требования как к характеристикам АЦП, так и вычислительным устройствам, осуществляющим обработку сигналов.
При нарушении этого условия, т.е.:
fs< 2∆F(2)
становится невозможным однозначное восстановление радиосигнала по его цифровым отсчетам, а в случае решения задачи измерения несущей частоты – получения однозначногозначения частоты. Для обозначения процесса дискретизации сигнала в соответствии с условием (2) в литературе используется термин субдскретизация.
Применение субдискретизации радиосигналов в цифровых приемниках позволяет существенно расширить диапазон частот обрабатываемых радиосигналов без увеличения тактовых частот АЦП и вычислительных устройств. Однако в этом случае возникает задача устранения неоднозначности представления радиосигнала в цифровом виде и, в частности, неоднозначности измерения несущей частоты сигнала.
В настоящем докладе рассмотрены алгоритмы измерения несущей частоты при субдискретизации радиосигналов.
Алгоритм измерения частоты действительного радиосигнала
Пусть на вход цифрового приемника поступает сигнал вида:
S(t) = A(t)cos(2πfct),(3)
где: A(t) – модулирующая функция, fc – несущая частота радиосигнала.
При аналого-цифровом преобразовании сигнала с частотой дискретизации, выбранной в соответствии с (2) и дальнейшем измерении несущей частоты возникает неоднозначность измерений. Способы устранения неоднозначности измерений известны и широко применяются в радиолокации, интерферометрии и т.д. [1]. В основе способов устранения неоднозначности измерений лежит идея реализации многошкальных или многоканальных измерительных систем [2].
Рассмотрим двухканальную схему цифрового приемника, решающего задачу измерения частоты радиосигнала (рисунок 1).

Рисунок 1
Входной сигнал S(t) с несущей частотой fcпоступает на пару АЦП, работающих с различными частотами дискретизации fs1 и fs2. На выходах АЦП формируются последовательности цифровых отсчетов сигнала S1(n) и S2(n), которые подвергаются быстрому преобразованию Фурье. В полученном амплитудном спектре сигнала в каждом из каналов находятся отсчеты с максимальный амплитудой, которые соответствуют измеренной частоте сигнала в первом (fизм1) и втором (fизм2) канале. Зависимость измеренной частоты fизм от частоты входного сигнала для первого и второго каналов приведена на рисунке 2.

Рисунок 2
В каждом из каналов частоте входного сигнала fc будут соответствовать наборы измеренных частот: fизм1 = {fc11, fc12,fc13, …} и fизм2 = { fc21, fc22,fc23, …}. Совпадающие значения в полученных наборах будут соответствуют истинной частоте сигнала. В примере, приведенном на рисунке 2:fc = fc13 = fc23.
В рассмотренном алгоритме существует недостаток, который заключается в следующем. При совпадении частоты сигнала с точками на частотной оси, в которых происходит пересечение графиков зависимостей измеренной частоты fизм от частоты входного сигнала для первого и второго каналов, устранение неоднозначности измерения частоты невозможно. Такая ситуация показана на рисунке 3.
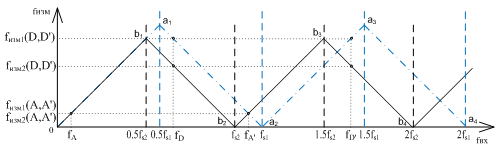
Рисунок 3
Допустим, частота входного сигнала fc = fА’. При этом : fизм1 = fизм2. Однако при fc = fА также соблюдается равенство fизм1 = fизм2. Аналогичная ситуация складывается при fc = fD’ = fD.
Указанного недостатка лишен алгоритм измерения частоты комплексного радиосигнала.
Алгоритм измерения частоты комплексного радиосигнала
Схема цифрового приемника, решающего задачу измерения несущей частоты комплексного радиосигнала, приведена на рисунке 4.

Рисунок 4
Каждый из каналов такого приемника содержит пару АЦП, на входы которых поступают синфазная SI(t) и квадратурная SQ(t) составляющая входного радиосигнала. В отличие от рассмотренной ранее схемы, быстрое преобразование Фурье в каждом канале выполняется для отсчетов комплексного сигнала SI1(n) и SQ1(n) в первом канале, и SI2(n) и SQ2(n) во втором канале. В остальном алгоритм обработки сигнала соответствует рассмотренному выше.
При комплексном представлении радиосигнала зависимость измеренной частоты fизм от частоты входного сигнала для первого и второго каналов будет выглядеть так, как это показано на рисунке 5.
В приведенном на рисунке 5 примере fc = fc13 = fc23. Анализ возможных ситуаций при устранении неоднозначности измерения частоты показал, что “проблемные” точки на частотной оси, в которых неоднозначность измерения не устраняется, отсутствуют.
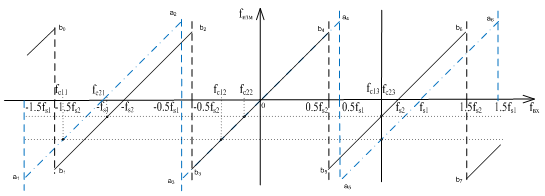
Рисунок 5
Выводы
Алгоритм измерения несущей частоты при субдикретизации действительного радиосигнала в двухканальном цифровом приемнике имеет недостаток, связанный с наличием частот сигнала, при которых происходят неоднозначные измерения. Такой недостаток возможно устранить увеличением числа измерительных каналов либо переходом к квадратурной обработке радиосигнала. Как и в любой многошкальной измерительной системе, устранение неоднозначности измерения частоты радиосигнала возможно в ограниченном диапазоне. Одной из ближайших задач исследований рассмотренных алгоритмов является оценка границ диапазона измерения несущей частоты радиосигнала при различных соотношениях частот дискретизации, а также различном числе точек БПФ.
Список литературы:
- Трухачев А.А. Радиолокационные сигналы и их применения. – М.: Воениздат, 2005. – 320 с.
- Собцов Н.В. Оценка максимального правдоподобия в многошкальной фазовой измерительной системе. Радиотехника и электроника, 1973, т.18, №6, с.1180 – 1186.[schema type=»book» name=»АЛГОРИТМЫ ИЗМЕРЕНИЯ НЕСУЩЕЙ ЧАСТОТЫ В ЦИФРОВЫХ ПРИЕМНИКАХ ПРИ СУБДИСКРЕТИЗАЦИИ РАДИОСИГНАЛОВ» description=»В докладе рассмотрены алгоритмы измерения несущей частоты радиосигналов. Алгоритмы используют два канала аналого-цифрового преобразования и быстрого преобразования Фурье с различными частотами дискретизации.» author=»Николаев Андрей Николаевич, Белугина Анастасия Александровна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-29″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.04.2015_04(13)» ebook=»yes» ]

