- Введение
Стандарты мобильных сетей четвёртого поколения (4G) предоставляют абонентам высокоскоростные услуги (мультимедийные сервисы, видеозвонки и видеоконфернции, интерактивные онлайн-приложения и др.) и требуют обеспечения гарантированного качества обслуживания QoS (англ. Quality of Service). Важной задачей является эффективное управление трафиком систем мобильной связи, для чего необходима оценка показателей качества (пропускная способность, потери, задержка и др.). Для решения данной задачи служат методы математического моделирования, одним из которых является анализ сетей массового обслуживания (СеМО), показавший свою эффективность при моделировании инфокоммуникационных систем различной размерности, топологии и назначения.
- Понятие сети массового обслуживания
Сетью массового обслуживания называется совокупность конечного числа систем массового обслуживания (СМО), в которой циркулируют сообщения, переходящие в соответствии с маршрутной матрицей из одной СМО в другую [1, 3, 5]. Маршрутная матрица содержит вероятности перехода заявки из одного узла в другой, является стохастической, зависит от вида СеМО и определяет её топологию:
![]() (1)
(1)
где N – количество узлов сети. Стохастичность матрицы определяется выполнением условий:
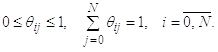 (2)
(2)
Пример СеМО из пяти СМО представлен на рисунке 1.
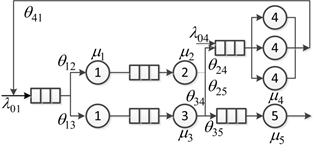
Рисунок 1. Пример СеМО
Сети массового обслуживания могут быть открытыми, замкнутыми и смешанными. Открытыми называются СеМО, имеющие бесконечный внешний источник заявок и сток, через который заявки покидают сеть после облуживания. В каждый момент времени в сети может находиться произвольное число заявок. В замкнутой СеМО отсутствует внешний источник-сток заявок и количество циркулирующих по сети заявок постоянно. Смешанные СеМО обладают свойствами и тех и других.
Сети массового обслуживания могут различаться по наличию нескольких классов заявок. Заявки, обладающие одинаковыми свойствами – распределением времени обслуживания, вероятностями перехода, дисциплиной обслуживания, принадлежат одному классу. Сети, в которой существует только один класс заявок, называются однородными, а сети с более чем одним классом заявок – неоднородными. В дальнейшем для простоты будем рассматривать однородные СеМО.
Марковские СеМО характеризуются показательным распределением времени обслуживания для обслуживающих приборов всех узлов сети. Сети, в которых распределение времени обслуживания отличается от показательного, называются СеМО общего вида [1, 3–5].
Описание СеМО определяется вектором [4]:

- СеМО в мультипликативной форме
Отправной точкой для анализа СеМО является понятие её состояния: ![]() , где
, где ![]() – количество заявок в i-й СМО, для замкнутой СеМО выполняется равенство:
– количество заявок в i-й СМО, для замкнутой СеМО выполняется равенство: ![]() . Распределение вероятностей состояний обозначим:
. Распределение вероятностей состояний обозначим: ![]() , с учётом нормирующего условия:
, с учётом нормирующего условия: ![]() [3, 5].
[3, 5].
Наиболее важную роль в теории сетей массового обслуживания играют СеМО, стационарное распределение которых имеет мультипликативную форму, поскольку для них вероятностно-временные характеристики могут быть получены простым способом.
3.1. Сети Джексона
Теорема Джексона гласит, что для открытой эргодической СеМО стационарное распределение вероятностей состояний может быть получено в мультипликативной форме [6]:

3.2. Сети Гордона-Ньюэлла
Гордон и Ньюэлл расширили результаты, полученные Джексоном, на замкнутые марковские сети [5].
Рассмотрим замкнутую СеМО, с конечным пространством состояний:
Рассмотрим пример на рисунке 3.

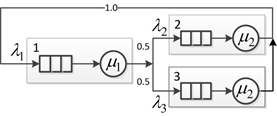
Рисунок 3. Пример замкнутой СеМО
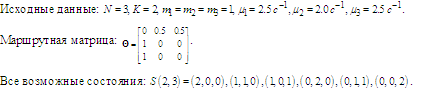
Определяем коэффициенты переходов и из выражений (5) и (6):

Далее можно вычислить коэффициенты загрузки узлов и другие сетевые характеристики из [2–5].
3.3. Алгоритм свёртки для анализа однородной замкнутой СеМО
Для сетей большой размерности со сложной топологией и большим количеством заявок расчёт нормализующей константы (12) и стационарного распределения вероятностей состояний СеМО (11) требует значительных вычислительных ресурсов и временных затрат. Поэтому на практике используют специальные методы расчёта, одним из которых является рекуррентный метод Бузена, основанный на алгоритме свёртки [1, 6].
Введём обозначение:

Далее определяются коэффициенты загрузки узлов и другие характеристики из [2–5].
Рассмотрим пример из раздела 3.2.
Начнём с расчёта коэффициентов переходов и , из (13):

Далее можно применить формулы расчёта параметров СМО типа M/M/1 для получения характеристик моделируемой системы [2].
- Заключение
Для оценки показателей качества в сетях мобильной связи применяются методы математического моделирования, наиболее эффективным из которых является анализ сетей массового обслуживания. Цель моделирования, сложность и размерность инфокоммуникационной системы оказывают влияние на выбор как типа, топологии и параметров моделирующей СеМО, так конкретного алгоритма, реализующего расчёт её характеристик. Кроме того, для построения аналитической модели необходимо учитывать вычислительный ресурс, имеющийся в наличии у разработчика.
Список литературы:
- Вишневский В.М. Теоретические основы проектирования компьютерных сетей. М.: Техносфера, 2003. 512 с.
- Клейнрок Л. Теория массового обслуживания. М: Машиностроение, 1979. 432 c.
- Кокорева Е.В. Анализ сетей массового обслуживания: учебно-методическое пособие. Новосибирск: СибГУТИ, 2015. 39 с.
- Ярославцев А.Ф. Компьютерные технологии в науке и производстве: учебное пособие. Т. 2. Новосибирск: ГОУ ВПО «СибГУТИ», 2009. 500 с.
- Bolch G., Greiner S., de Meer H., Trivedi K. S. Queueing Networks and Markov Chains: Modeling and Performance Evaluation with Computer Science Applications. 2nd Edition. John Wiley & Sons, 2006. 896 p.
- Jackson J. R. Networks of waiting lines // Oper. Res. 1957. V.5, № 4. P. 518-521.[schema type=»book» name=»ПРИМЕНЕНИЕ АЛГОРИТМА СВЁРТКИ ДЛЯ АНАЛИЗА СИСТЕМ МОБИЛЬНОЙ СВЯЗИ» description=»Современные системы мобильной связи требуют гарантированного качества обслуживания. Математическое моделирование применяется для оценки показателей качества. Наиболее адекватный метод аналитического моделирования в настоящее время предоставляет математический аппарат теории сетей массового обслуживания, рассмотренный в данной статье.» author=»Кокорева Елена Викторовна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2016-12-22″ edition=»euroasian-science.ru_25-26.03.2016_3(24)» ebook=»yes» ]

