Многие научно-технические задачи описываются уравнениями газодинамики. Поскольку они имеют нелинейную форму, точные или приближенные аналитические решения могут быть получены лишь для ограниченного числа частных случаев. Поэтому для их решения обычно применяют численные методы.
Одним из способов решения системы уравнений газодинамики является метод CSPH‑TVD (Combined Smooth Particle Hydrodynamics — Total Variation Diminishing), впервые предложенный в работе [2, с. 282] для уравнений мелкой воды. Он основан на последовательном применении лагранжева (SPH) и эйлерова (TVD) подходов.
В дальнейшем было сделано обобщение этой численной схемы для уравнений идеальной газодинамики [1, с. 60]. В работе [3, с. 22] проанализировано влияние ограничителей наклонов и способов приближенного решения задачи Римана на точность метода CSPH‑TVD.
В данной работе приведены результаты исследования точности и сходимости для методов CSPH‑TVD, MUSCL [9, с. 101], PPM [4, с. 174] и WENO [6, с. 202].
Динамику невязкого нетеплопроводного газа в отсутствии внешних сил для одномерного случая можно описать с помощью уравнений

На рисунке 1 показаны полученные с использованием метода CSPH‑TVD распределения плотности и давления в момент времени t = 0.15 для различного числа расчетных ячеек в сравнении с точным решением.
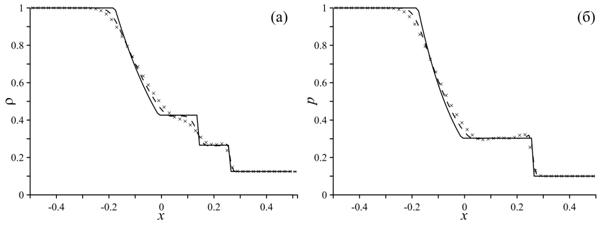
Рисунок 1. Распределение плотности (а) и давления (б) в момент времени . Крестиками показано численное решение для N = 50, пунктирной линией — для N = 100, сплошной линий показано точное решение
Относительные ошибки и порядки сходимости для рассматриваемых методов представлены в таблицах 1, 2, 3. Отметим, что для вычислений использовались только значения в области x < xο, не содержащей разрывов первого рода.
Таблица 1
Относительные ошибки и порядки сходимости в норме L1
| Схема | E50 | O50-100 | E100 | O100-200 | E200 | O200-400 | E400 |
| MUSCL | 1.55 | 1.03 | 0.76 | 0.99 | 0.38 | 1.0 | 0.19 |
| PPM | 1.02 | 1.01 | 0.5 | 0.99 | 0.25 | 1.02 | 0.12 |
| WENO | 1.99 | 0.96 | 1.03 | 0.94 | 0.53 | 0.98 | 0.27 |
| CSPH‑TVD | 3.3 | 0.78 | 1.92 | 0.8 | 1.1 | 0.83 | 0.62 |
Таблица 2
Относительные ошибки и порядки сходимости в норме L2
| Схема | E50 | O50-100 | E100 | O100-200 | E200 | O200-400 | E400 |
| MUSCL | 0.56 | 1.5 | 0.2 | 1.43 | 0.07 | 1.47 | 0.03 |
| PPM | 0.45 | 1.5 | 0.16 | 1.4 | 0.06 | 1.45 | 0.02 |
| WENO | 0.73 | 1.43 | 0.27 | 1.38 | 0.1 | 1.42 | 0.04 |
| CSPH‑TVD | 1.19 | 1.19 | 0.5 | 1.25 | 0.21 | 1.27 | 0.09 |
Таблица 3
Относительные ошибки и порядки сходимости в норме
| Схема | E50 | O50-100 | E100 | O100-200 | E200 | O200-400 | E400 |
| MUSCL | 0.32 | 1.97 | 0.08 | 1.69 | 0.02 | 1.82 | 0.01 |
| PPM | 0.36 | 1.94 | 0.09 | 1.67 | 0.03 | 1.76 | 0.01 |
| WENO | 0.47 | 1.86 | 0.13 | 1.69 | 0.04 | 1.7 | 0.01 |
| CSPH‑TVD | 0.73 | 1.75 | 0.22 | 1.61 | 0.07 | 1.58 | 0.02 |
Из таблиц 1, 2, 3 следует, что относительные ошибки и порядки сходимости всех рассмотренных численных схем довольно близки для рассматриваемого случая (3), что может быть обусловлено наличием в структуре решения слабого разрыва (разрыва второго рода), которые присутствуют в решениях практически всех газодинамических задач. Отметим, что это как раз и позволяет понять свойства численных схем в условиях реальных расчетов, а не синтетических тестов с переносом гладких профилей (вопрос о точности численного решения в окрестности сильного разрыва рассматривать здесь не будем).
Проведенное исследование показывает, что метод CSPH‑TVD имеет сопоставимые с популярными эйлеровыми численными схемами точность и сходимость. Отличительной его чертой является возможность расчетов на границе с вакуумом без необходимости дополнительной регуляризации [2, с. 282].
Работа выполнена при финансовой поддержке РФФИ и Администрации Волгоградской области (гранты 16-07-01037 А, 16-02-00649 А, 15-02-06204 А, 15-45-02655-р_поволжье_а)
Список литературы:
- Жумалиев, А.Г. Численная схема cSPH‑TVD: моделирование фронта ударной волны / А.Г. Жумалиев, С.С. Храпов // Вестник Волгоградского государственного университета. Серия 1. Математика. Физика. — 2012. — № 2 (17). — C. 60‑67.
- Численная схема для моделирования динамики поверхностных вод на основе комбинированного SPH‑TVD подхода / С.С. Храпов, А.В. Хоперсков, Н.М. Кузьмин, А.В. Писарев, И.А. Кобелев // Вычислительные методы и программирование: новые вычислительные технологии. — 2011. — Т. 12, № 1. — C. 282‑297.
- Численная схема cSPH‑TVD: исследование влияния ограничителей наклонов / Н.М. Кузьмин, А.В. Белоусов, Т.С. Шушкевич, С.С. Храпов // Вестник Волгоградского государственного университета. Серия 1. Математика. Физика. — 2014. — № 1 (20). — C. 22‑34.
- Colella, P. The piecewise parabolic method (PPM) for gas-dynamical simulations / P. Colella, P.R. Woodward // Journal of Comutational Physics. — 1984. — Vol. 54, No. 1. — P. 174‑201.
- Harten, A. On upstream differencing and Godunov type methods for hyperbolic conservation laws / A. Harten, P. Lax, B. van Leer // SIAM Review. — 1983. — Vol. 25, No. 1. — P. 35‑61.
- Jiang, G.‑S. Efficient implementation of weighted ENO schemes / G.‑S. Jiang, C.W. Shu // Journal of Comutational Physics. — 1996. — Vol. 126, No. 1. — P. 202‑228.
- Lax, P. D. Weak solutions of nonlinear hyperbolic equations and their numerical computation / P.D. Lax // Communications on Pure and Applied Mathematics. — 1954. — Vol. 7, No. 1. — P. 159‑193.
- van Leer, В. Towards the ultimate conservative difference scheme. III. Upstream-centered finite-difference schemes for ideal compressible flow / В. van Leer // Journal of Computational Physics. — 1977. — Vol. 23, № 3. — P. 263‑275.
- van Leer, B. Towards the ultimate conservative difference scheme. V. A Second order sequel to Godunov’s method / B. van Leer // Journal of Computational Physics. — 1979. — Vol. 32, No. 1. — P. 101‑136.[schema type=»book» name=»СРАВНЕНИЕ ТОЧНОСТИ И СХОДИМОСТИ РАЗНОСТНЫХ СХЕМ ДЛЯ РЕШЕНИЯ УРАВНЕНИЙ ГАЗОДИНАМИКИ» description=»В работе представлены результаты исследования точности и сходимости методов CSPH TVD, MUSCL, PPM и WENO для решения уравнений идеальной газодинамики в одномерном случае на примере задачи о распаде разрыва. Показано, что все указанные методы дают очень близкие результаты.» author=»Кузьмин Николай Михайлович, Храпов Сергей Сергеевич, Бутенко Мария Анатольевна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-13″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.12.16_33(2)» ebook=»yes» ]

