Описание модели.
Многослойный персептрон состоит из множества сенсорных элементов (входных узлов или узлов источника), которые образуют входной слой; одного или нескольких скрытых слоев вычислительных нейронов и одного выходного слоя нейронов. Входной сигнал распространяется по сети в прямом направлении, от слоя к слою [1].
Многослойные персептроны успешно применяются для решения разнообразных сложных задач. При этом обучение с учителем выполняется с помощью такого популярного алгоритма, как алгоритм обратного распространения ошибки. Этот алгоритм основывается на коррекции ошибок.
Каждый нейрон сети имеет нелинейную функцию активации. Функция активации должна обладать несколькими важными характеристиками: непрерывностью, дифференцируемостью и являться монотонно неубывающей [2]. Более того, ради эффективности вычислений, желательно, чтобы её производная легко находилась. Самой популярной наиболее часто используемой функций, удовлетворяющей этим требованиям, является сигмоидальная, определяемая логистической функцией
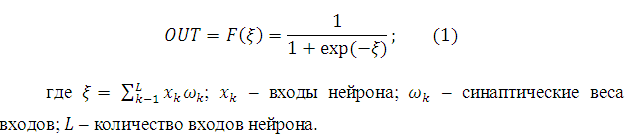
Обучение методом обратного распространения ошибки предполагает два прохода по всем слоям сети: прямого и обратного. Принцип функционирования алгоритма обратного распространения ошибки, заключается в использовании метода градиентного спуска и корректировки весов, для минимизации ошибки нейронной сети. Формула коррекции весов для выходного слоя имеет вид

Модификация модели.
В настоящее время не существует общего алгоритма определения структуры ИНС, подходящего для каждой рассматриваемой проблемы. Часто такую структуру выбирают методом «проб и ошибок», который зачастую отнимает у исследователей много времени [3]. Поскольку для каждой структуры необходимо подбирать значения весовых коэффициентов, то ускорение этого подбора должно ускорить процесс обучения ИНС.
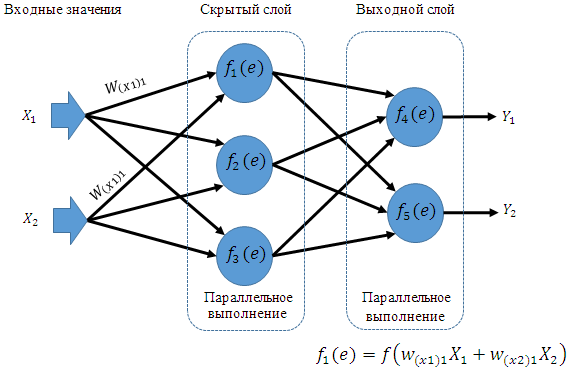
Рисунок 1. Распространение сигнала при параллельном обучении.
Параллельная программа имеет особый принцип работы. В отличие от последовательной, где одновременно выполняется только одно действие, в параллельных программах одновременно выполняются сразу несколько операций. Для этого необходимо основную задачу разбить на подзадачи, которые могут выполняться независимо друг от друга (не используя при этом данные, необходимые для выполнения других задач). Следовательно, проектировать алгоритм необходимо с учетом этой особенности. При разделении алгоритма на блоки, которые будут выполняться параллельно, необходимо также учитывать то, что блоки должны быть равными, т.е. их выполнение должно занимать одинаковое количества времени. А также следует помнить, что при распараллеливании появляются временные затраты на передачу данных. Обычно пересылки требуют достаточно большого времени для своего осуществления, поэтому другой важной целью распараллеливания является минимизация объема и количества необходимых пересылок данных [4].
В данной работе предлагается модель, основанная на параллельном прохождении нейронов, как при прямом распространении сигналов, так и в обратном направлении при корректировке весов. Тот факт, что нейроны, находящиеся в одном слое, не зависят друг от друга (на них влияют только выходные параметры предыдущего слоя и весовые коэффициенты), позволяет распараллелить вычислительный процесс. Распространение сигналов при параллельной интерпретации алгоритма схематически обозначено на рисунке Рисунок 1.
Таблица 1. Принципы выполнения блоков алгоритма обучения.
| Название блока алгоритма обучения нейронной сети методом обратного распространения ошибки | Принцип выполнения |
| Входные данные | Последовательно |
| Распространение сигнала по нейросети
(вычисление выходного значения) |
Параллельно |
| Вычисление погрешности | Последовательно |
| Проверка погрешности | Последовательно |
| Обратное распространение ошибки (корректировка весовых коэффициентов) | Параллельно |
В таблице Таблица 1 представлена характеристика блоков алгоритма по принципу выполнения. Для реализации распараллеливания в данной работе была применена технология CUDA.
Результат
В данной работе проведен анализ популярного метода обучения ИНС с обратным распространением ошибки. Выявлены блоки алгоритма, математически независимы друг от друга и предложен алгоритм с параллельной реализацией вычислений. Полученный алгоритм имеет преимущество по времени вычисления, т.к. время прохождения всего слоя равно времени прохождения одного нейрона.
Список литературы:
- Саймон Хайкин. Нейронные сети. Полный курс. Второе издание. // Университет McMaster Гамильтон, Онтарио, Канада. 2006. С. 219-333.
- Laurene V. Fausett. Fundamentals of Neural Networks: Architectures, Algorithms and Applications. Prentice-Hall, 1994.
- Арзамасцев А. А., Крючин О. В., Азарова П. А., Зенкова Н. А. Универсальный программный комплекс для компьютерного моделирования на основе искусственной нейронной сети с самоорганизацией структуры // Вестник Тамбовского университета. Серия Естественные науки и технические науки. Тамбов, 2006. Т. 11. Вып. 5. С. 372-375.
- Антонов А. С. Введение в параллельные вычисления. М., 2002.[schema type=»book» name=»ОПТИМИЗАЦИЯ АЛГОРИТМА ОБУЧЕНИЯ ИНС» description=»В данной статье предлагается вариант оптимизации алгоритма обучения искусственной нейронной сети с обратным распространением ошибки путем распараллеливания процесса обучения. Производится анализ алгоритма обучения, выявляются однотипные подпроцессы, входные и выходные параметры которых не зависят друг от друга, что позволяет выполнять эти задачи одновременно.» author=»Таранов Роман Владимирович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2016-12-21″ edition=»euroasian-science.ru_25-26.03.2016_3(24)» ebook=»yes» ]

