На многих производствах одним из интенсивных источников аэродинамического шума, превышающего нормативные значения, являются системы транспортирования на воздушной подушке, предназначенные для межоперационного перемещения изделий. Специфические особенности аэродинамических процессов воздушной подушки в некоторых производствах делают её незаменимой [8, 9, 10, 11]. Однако требования производственной безопасности диктуют необходимость правильного проектирования производственных систем транспортирования на воздушной подушке, обеспечивающих малый уровень шума, не превышающий допустимых значений [14].
В установившемся течении в воздушной подушке с позиции эргодической гипотезы [13, 15] возникают стационарные процессы вихреобразования, порожденные вязкостью потока, что приводит к возникновению аэродинамических звуковых потоков. Физическая картина взаимодействия турбулентного потока со звуковыми волнами в тонком зазоре между двумя параллельными плоскостями многогранна и характеризуется взаимозависимостью различных факторов. К этим факторам можно отнести структуру вихрей, физические и акустические характеристики плоскостей, аэродинамические и термодинамические параметры потока, форму и расположение питающих отверстий (сопел), создающих воздушную подушку. В итоге в результате этого взаимодействия формируется звуковой поток, основная энергетическая составляющая которого поступает через боковые грани воздушной подушки. Как показывает эксперимент и анализ функционирования воздушной подушки, величина уровня звука остается постоянной для стационарных процессов, параметры которых не изменяются во времени. Этими параметрами являются давление в пневмокамере, вес транспортируемых предметов, проходное сечение сопел, температура. При изменении какого либо параметра режим течения изменяется и, соответственно, изменяются характеристики акустического поток. Наблюдается корреляционная связь между изменениями параметров воздушной подушки и изменениями акустических показателей звуковых потоков. Для турбулентных потоков важными показателями являются турбулентная вязкость и геометрическая характеристика – «путь перемешивания». Таким образом, используя эти показатели можно на основе аэродинамической модели течения построить модель уровня звука, порождаемого этим течением.
В классической акустике генерацию звука описывают с помощью неоднородного волнового уравнения, правая часть которого определяет источники звука, их распределение в пространстве и структуру. Задачей является получение на основе классических уравнений механики жидкости такого уравнения, которое моделировало бы величину уровня шума аэродинамического происхождения [1, 2, 3]. В монографии [7] Кузнецов В.М. отмечает, что генерация и распространение возмущений в движущейся жидкой среде могут быть описаны с помощью уравнений аэроакустики, которые получены из уравнений движения жидкости. Однако при выводе уравнений аэроакустики используются методы комбинирования отдельными членами уравнения, методы упрощения и приближения. Результатами этих преобразований являются модели и теории, которые могут показаться несколько противоречивыми. Наиболее эффективными являются модели и теории, дающие возможность получения уравнения аэроакустики, дающие практический результат.
Рассмотрим турбулентный поток воздуха, имеющий место в воздушной подушке. Особенностью такого течения является наличие твердых поверхностей, способствующих формированию слоистого течения воздуха – так называемый сдвиговый поток, в котором скорость зависит только от поперечных координат. Кроме того, течение в воздушной подушке обладает свойствами течения в канале и, в некоторой степени, свойствами свободного течения.
Влиянием вязкости и теплопроводности в части распространения звука можно пренебречь, помня, однако, что роль вязкости является весьма существенной в образовании исходного состояния среды, в которой генерируется и распространяется звук.
Для получения уравнений, описывающих генерацию звука в неоднородной движущейся среде, рассмотрим методику, предложенную Блохинцевым Д.И. [4, 5]. Запишем уравнения движения, уравнение неразрывности и уравнение для энтропии сжимаемой жидкости без учета вязкости

Традиционно, основные характеристики области течения воздуха представляются в виде суммы двух величин: одна величина соответствует среднему значению характеристики, а другая – является пульсационной составляющей. Характеристики скорости, плотности, давления и энтропии запишем в виде

При слабых колебаниях параметров, представленных в соотношении (5), происходит изоэнтропийное сжатие или расширение газа, поэтому давление и плотность связаны уравнением , откуда



Уравнения (14) представляют собой уравнения для потенциала скорости малых возмущений применительно к течению воздуха в объеме. Эти уравнения записаны относительно трех декартовых координат и позволяют определять акустические характеристики объемных воздушных потоков при условии наличия границ, рассматриваемого течения. В общем виде решение этой системы уравнений представляет собой сложную задачу. Однако учет реальных начальных и граничных условий может существенно упростить эти уравнения.
Рассмотрим частный случай воздушного течения в тонком зазоре между плоскостями. Воздушная подушка в этом случае формируется одиночным щелевым отверстием, расположенным под изделием прямоугольной формы. Их взаимное расположение показано на рис. 1.
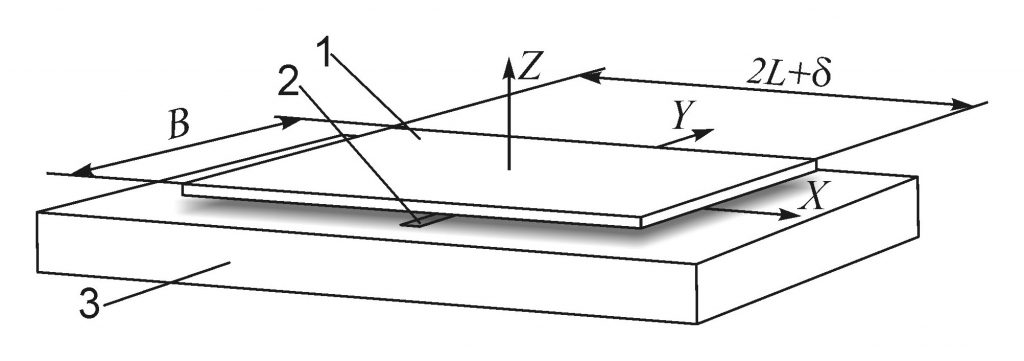
Рисунок 1. Схематичное изображение взаимного расположения щелевого отверстия и изделия на воздушной подушке. 1 – изделие, 2 – щелевое отверстие, 3 – пневмокамера.
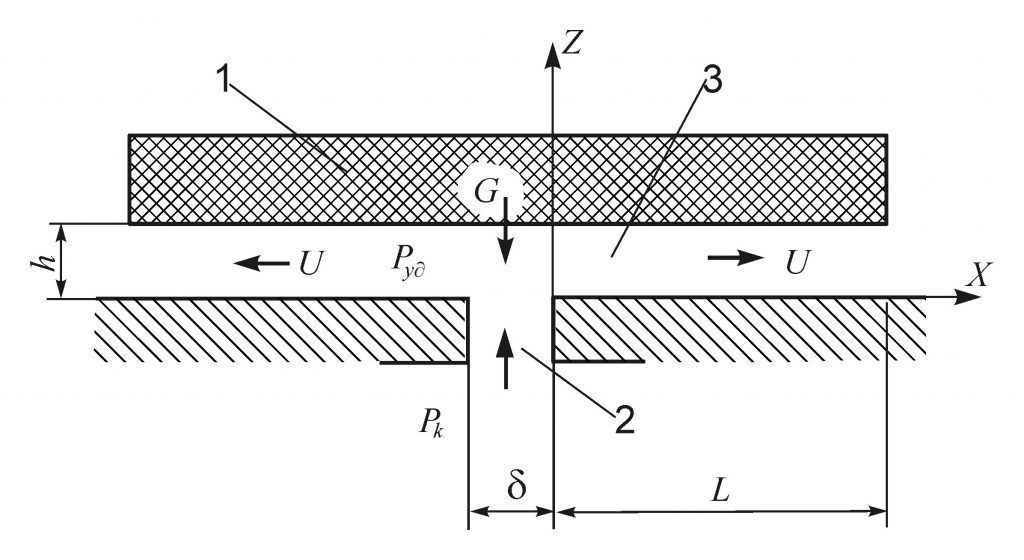
Рисунок 2. Расчетная схема для определения гидродинамических характеристик воздушной подушки. 1 – изделие, 2 – щелевое отверстие, 3 – воздушная подушка.

На расчетной схеме (рис. 2) представлены основные размеры системы, рабочее отверстие и изделие. Для течения воздуха под изделием запишем систему уравнений с учетом ряда допущений применяемых, обычно, для плоских течений.


В уравнениях из табл. 1 присутствуют соотношения, содержащие динамическую вязкость, которая может быть заменена турбулентной вязкостью , так как порядок динамической и турбулентной вязкости совпадает.
Гипотеза Прандтля [12] о пути перемешивания является наиболее предпочтительной, так как позволяет выполнять расчет характеристик турбулентных течений. Одной из этих характеристик является длина пути перемешивания . Хотя длина пути перемешивания и не является физической постоянной для каждой жидкости в отличие от молекулярных коэффициентов вязкости и теплопроводности, однако, она как показывают опытные данные, не зависит от параметров потока. Длина пути перемешивания в основном является функцией координаты . Принимая простейшую гипотезу, что вблизи стенки длина пути перемешивания пропорциональна расстоянию от стенки , можно связать, следуя Прандтлю, скорость в турбулентном потоке с турбулентной вязкостью [5]. Тогда

Уравнение (18) определяет уровень аэродинамического шума создаваемого воздушной подушкой, формируемой одиночным щелевым отверстием
Список литературы:
- Исакович М.А. Общая акустика. М.: Наука, 1973. – 496 с.
- Блохинцев Д.И. Акустика неоднородной движущейся среды. М.: Наука. – Главная редакция физико-математической литературы, 1981. – 208 с.
- Мурзинов В.Л. Снижение шума в устройствах транспортирования на воздушной подушке. Воронеж: Росинформресур, 2008. – 196 с.
- Мунин А.Г., Кузнецов В. М., Леонтьев Е. А. Аэродинамические источники шума. М.: Машиностроение, 1981. – 248 с.
- Кузнецов В.М. Идентификация источников шума турбулентной струи // Акустический журнал. – 2012, № 4. С. 498 – 508.
- Мурзинов В.Л. Автоматическая стабилизация толщины воздушной подушки и снижение шумоизлучения в пневмоконвейерах // Автоматизация и современные технологии. – 2008, №10. – С. 3–9.
- Кузнецов В.М. Основы теории шума турбулентных струй. М.: ФИЗМАТЛИТ, 2008. – 240 с.
- Мурзинов В.Л. Пневмоконвейер со струйным управление скоростью и направлением движения транспортируемых изделий. – В кн.: Подъемно-транспортное оборудование. М.: ЦНИИТЭИтяжмаш,1980, №21. – С.5-8.
- Мурзинов В.Л. Пневмоконвейер со струйным управлением. – В. кн.: Подъемно-транспортное оборудование. М.: ЦНИИТЭИтяжмаш,1981, №10. – С.8-10.
- Битюков В.К., Колодежнов В.Н. Кущев Б.И., Мурзинов В.Л. Пневмоконвейеры с автоматической стабилизацией скорости транспортируемых изделий. // Механизация и автоматизация производства. – 1983, №1. – с.26.
- Битюков В.К., Колодежнов В.Н., Мурзинов В.Л. Самонастраивающиеся пневматические конвейеры на воздушной прослойке. // Механизация и автоматизация производства. – 1981, №11. – С.18-20.
- Теория турбулентных струй / Г.Н. Абрамович, Т.А. Гиршович, С.Ю. Крашенинников, А.Н. Секундов, И.П. Смирнова; Под ред. Г.Н. Абрамовича. М.: Наука, 1984. – 717 с.
- Ордынцев В.М. Математическое описание объектов автоматизации. М.: Машиностроение, 1965. – 360 с.
- Борьба с шумами на производстве/ под ред. Е.Я. Юдина. М.: Машиностроение, 1985. – 512 с.
- Мурзинов В.Л. Метод снижения аэродинамического шума в пневмоконвейерах [Текст] // Безопасность труда в промышленности. – 2007, №3. – С.54–58.[schema type=»book» name=»МОДЕЛИРОВАНИЕ АЭРОДИНАМИЧЕСКОГО ШУМА ВОЗДУШНОЙ ПОДУШКИ» description=»Воздушные потоки в природе, в технических устройствах, в производственных системах транспортирования на воздушной подушке генерируют аэродинамических шум, который является негативным фактором с позиции экологии. Аэродинамический шум, генерируемый воздушным потоком, возникает благодаря турбулентности этого потока. Моделирование аэродинамического шума можно осуществлять методом преобразования уравнений движения, неразрывности и энтропии для воздушных потоков. Представлены результаты построения модели потенциала скорости малых возмущений турбулентного потока в воздушной подушке. Показано соотношение, связывающее гидродинамические характеристики турбулентного потока с его акустическими характеристиками в воздушной подушке. Получена формула для инженерных расчётов уровня аэродина-мического шума, формируемого воздушной подушкой, образованной одиночным щелевым отверстием.» author=»Мурзинов Валерий Леонидович, Мурзинов Павел Валерьевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-02-20″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_25.07.15_07(16)» ebook=»yes» ]

