Введение. Аммиак исследовался во многих работах. В частности, в работах [4,14] приводятся данные по димерам аммиака; в работе [12] описываются структуры тримеров. Результаты расчетов структуры кристалла и ряда термодинамических параметров приведены в [1,3]. В работе [2] обсуждается уравнение состояния кристаллического аммиака, некоторые термодинамические параметры и фазовые диаграммы. Так же уравнения состояния обсуждается в работе [8], а в работах [5,6] приводятся значения модулей упругости и их производных по давлению при различных параметрах для кристаллического аммиака.
В твердой фазе аммиак представляет собой бесцветные кристаллы, образованные кубической решеткой, симметрия P213 [11]. Элементарная ячейка содержит четыре молекулы аммиака, находящиеся в локальной симметрии C3v. Помимо изучения водородных связей в аммиаке, которые проявляют нелинейность, исследование кристаллического аммиака имеет важное практическое значение для астрономии, т.к. в космическом пространстве присутствует значительное количество аммиака и, кроме того, аммиак находится в большом количестве на Уране и Нептуне. В настоящей работе основные расчеты выполнялись с помощью программного пакета CRYSTAL09 [9].
Цель работы – исследование структуры молекулы, димера, тримера и кристалла аммиака, исследование геометрических параметров молекул в элементарной ячейке, получение некоторых энергетических и термодинамических параметров.
Структура молекулы, димеров, тримеров и кристалла аммиака. Молекула аммиака имеет форму тригональной пирамиды с атомом азота в вершине. Полученные значения длины N-H связи в молекуле составляют 1,017 Å, валентные углы ∠HNH=106,4° в случаи использования базисов 3-1p1G и 6-31d1G [10], при использовании базисов TZVP длины N-H связей 1,011 Å, валентные углы ∠HNH=108,5°. Полученная структура димера аммиака в базисах 3-1p1G и 6-31d1G приведена на рисунке 1 а. Расстояния между атомами азота составляет 3,269 Å. При этом длина связи H2-N1 составляет 1,017 Å, валентный угол ∠H2N1H3=106,1°. Угол ∠H5N6N1=21,5°.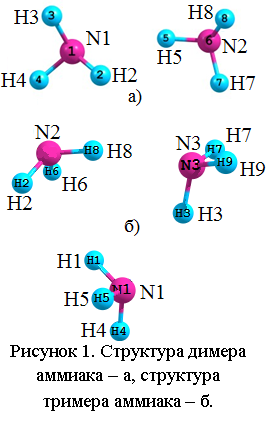 
Таким образом, геометрические параметры молекул в димере близки к тем же параметрам свободных молекул. Отличие от нуля угла HN—N свидетельствует о нарушении линейности водородной связи в димере. Это обстоятельство отмечается так же в работе [13].
Структура тримера аммиака приведена на рисунке 1 б. При использовании базисов TZVP расстояния R между атомами N1 и N2 составляет 3,487 Å, R(N1-N3)= 3,117 Å, R(N2-N3)= 3,237 Å. Длины N-H связей в молекулах составляет 1.012 Å, за исключением связей N2-H8 и N3-H3, они составляют 1.02 Å. Углы HNN так же отличны от нуля, и составляют ∠H3N3N1=13,18°, ∠H8N2N3=8,75°. При использовании базисов 3-1p1G и 6-31d1G R(N1-N2) =3,387 Å, R(N1-N3)=3,028 Å, R(N2-N3)=3,155 Å. Длины N-H связей в молекулах составляет 1.017 Å, за исключением связей N2-H8 и N3-H3, они составляют 1,026 Å, ∠H3N3N1=20,19°, ∠H8N2N3=8,14°. Таким образом, в тримере так же наблюдается нарушение линейности водородной связи, а геометрические параметры молекул тримера незначительно отличаются от тех же параметров свободных молекул.
Структура элементарной ячейки приведена на рисунке 2. По данным работы [1], в структурной фазе I, при давлении 0 Па и температуре 2 К постоянная решетки составляет 5,048 Å, объем элементарной ячейки 128,63 Å3.
По результатам расчетов настоящей работы, в структурной фазе I, при использовании потенциала B3LYP и базисов 3-1p1G для атомов водорода и 6-31d1G для атомов азота, постоянная решетки a=4,942 Å, отклонение от экспериментальных данных [1] составляет 2,10%. Объем элементарной ячейки V=120,685 Å3. Длина H-N связи в молекулах составляет 1,022 Å, валентные углы HNH составляют 107,1°. Угол NH—N составляет 159,8°. Плотность 0,937 г/см3.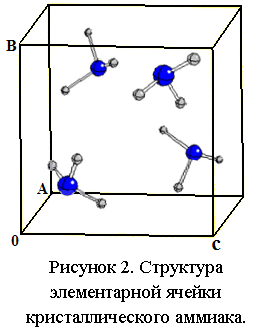 
При использовании базисов TZVP постоянная решетки a=4,955 Å (отклонение от экспериментальных данных [1] составляет 1,83%), объем элементарной ячейки V=121,69 Å3. Плотность 0,929 г/см3. Длина H-N связи в молекулах составляет 1.018 Å, валентные углы HNH составляют 107.9°. Угол NH—N составляет 159.7°. Данные параметры молекул хорошо согласуются с работой [1]. Углы HN—N составляют 14,48°.
Энергетические и термодинамические параметры. Полная энергия системы (димера, тримера, элементарной ячейки) рассчитывалась по формуле
EFULL=EL+E0+Edisp
где EL – энергия электронной системы, E0 – энергия нулевых колебаний, Edisp – дисперсионная энергия. Расчет дисперсионной энергии производился так же используемым программным пакетом, в котором реализована расчетная схема для дисперсионной энергии Grimme06 [7]. При её расчете использовались дисперсионные коэффициенты C6(H)=0.14 J*nm6/mol; C6(N)=1.23 J*nm6/mol; и радиусы Ван-Дер-Ваальса R(H)=1.09 Å; R(N)=1.61 Å. Дисперсионная энергия, полная энергия тримера и элементарной ячейки приведены в таблице 1. Заселенность N-H связи P, характеризующая прочность связи, а следовательно и предопределяющая энергию связи, так же приведена в таблице 1. Для оценки распределения заряда в молекулах получены значения избыточных зарядов на атомах δq.
Таблица 1.
Полная энергия, ат.ед. (EFULL), энергия нулевых колебаний, ат.ед. (E0), дисперсионная энергия, ккал/моль, (Edisp), заселенность N—H связи (P) в единицах элементарного заряда, избыточные заряды на атомах (δq), в единицах элементарного заряда.
|
|
Тример |
Кристалл |
||
| Базисы /
Параметр |
3-1p1G и 6-31d1G | TZVP | TZVP | 3-1p1G и 6-31d1G |
| EFULL | -169,47156 | -169,533365 | -226,1355 | -226,04648 |
| E0 | 0,110276 | 0,108508 | 0,155234 | 0,156022 |
| Edisp | -4,3568 | -3,7123 | -27,9988 | -19,3824 |
| P | 0.305 (N1-H1) 0.314 (N3-H3) | 0.391 (N1-H1) 0.401 (N3-H3) | 0,377 | 0,315 |
|
δq(N) |
-0.710 (N1) -0.729 (N2)
-0.738 (N3) |
-0.532 (N1) -0.550 (N2)
-0.576 (N3) |
0,581 |
0,809 |
|
δq(H) |
0,275 (H3)
0,281 (H8) 0,229 (H1) |
0,183 (H1)
0,231 (H3) 0,234 (H8) |
-0,194 |
-0,270 |
1 Ат.ед. = 27,211396 эВ.
В тримере заселенность N-H связей и избыточные заряды на атомах зависят главным образом от относительной ориентации линий химических связей различных молекул. Полная энергия димера, рассчитанного в базисах 3-1p1G и 6-31d1G составляет -112,9748 ат.ед. Энергия диссоциации димера на молекулы, полученная как разность полной энергии димера и полной энергии свободных молекул составила -3,67 ккал/моль. В работе [4] эта энергия составляет -3,2 ккал/моль. Дисперсионная энергия в работе [14] -0.52 ккал/моль, что отличается от расчетного значения (в настоящей работе -0,871 ккал/моль).
При исследовании кристалла аммиака так же получены значения изотермического модуля объемного сжатия B0, и его первая производная по объему B1 . полученные значения приведены в таблице 2. Использовались уравнения: уравнение состояние твердого тела в виде Birch–Murnaghan (BMEOS) [8], уравнение состояния в виде Vinet (VEOS).
Таблица 2.
Объем элементарной ячейки (V0), Å3; изотермический модуль объемного сжатия (B0), Гпа; производная B0 по давлению (B1).
|
|
V0 | B0 |
B1 |
|||
|
BMEOS |
116,947 | 137,328
132,0 [5,6] |
12,19 | 6,67
7,1 [5,6] |
5,96 |
5,02 5,97 [5,6] |
| VEOS | 116,946 | 12,20 | 5,96 | |||
По результатам расчетов, молярная теплоемкость кристалла при постоянном давлении Cp, при использовании базисов 3-1p1G для атомов водорода и 6-31d1G для атомов азота, составила 134,53 Дж*моль-1*К-1, энтропия S=117,95 Дж*моль-1*К-1. При использовании базисов TZVP, Cp=135,35 Дж*моль-1*К-1, S= 109,17 Дж*моль-1*К-1.
Заключение. В результате проведенного исследования структуры молекулы, димера, тримера и кристалла аммиака установлено, что полученные геометрические параметры соответствующих структур и энергетические параметры удовлетворительно согласуются с литературными данными. Полученные изотермические модули объемного сжатия отличаются от литературных данных. Для димеров угол HN—N составляет 13,18° и 8,75°; в тримере угол HN—N составляет 20,19° и 8,14°, в зависимости от используемого базиса. В кристаллической решетке угол HN—N составляет 14,48°. Таким образом, в димере, тримере и кристалле аммиака наблюдается нарушение линейности водородной связи.
Особая благодарность выражается научному руководителю – Журавлеву Юрию Николаевичу, д.ф-м.н, профессору, за постановку задачи и полезные
консультации при обсуждении полученных результатов.
Список литературы:
- Fortes A. D. Hydrogen bonding in solid ammonia from ab initio calculations /A. D. Fortes, J. P. Brodholt, I. G. Wood, and L. Voadlo // The Journal of Chemical Physics (2003) 118, 5987; doi: 10.1063/1.1555630.
- Mandy Bethkenhagen. Equation of state and phase diagram of ammonia at high pressures from ab initio simulations / Mandy Bethkenhagen, Martin French, and Ronald Redmer // The Journal of Chemical Physics (2013) 138, 234504; doi: 10.1063/1.4810883.
- Loveday J. S. Structure of Deuterated Ammonia IV / J. S. Loveday, R. J. Nelmes, and W. G. Marshall // Volume 76, number 1 Physical Review Letters.
- Tobias Benighaus. Semiempirical Double-Hybrid Density Functional with Improved Description ofLong-Range Correlation / Tobias Benighaus, Robert A. DiStasio, Jr., Rohini C. Lochan, Jeng-Da Chai, and Martin Head-Gordon // Phys. Chem. A 2008, 112, 2702-2712.
- Fortes A.D. Hydrogen bonding in solid ammonia from ab initio calculations / A. D. Fortes, J. P. Brodholt, I. G. Wood, and L. Vocˇadlo // Journal of Chemical Physics 2003. V. 118, N 13. P. 5987.
- Datchi F. Solid ammonia at high pressure: A single-crystal x-ray diffraction study to 123 GPa / F. Datchi, S. Ninet, M. Gauthier, A. M. Saitta, B. Canny, and F. // Physical Review B 2006. V.73, N 174111.
- S. Grimme. Semiempirical gga-type density functional constructed with along range dispersion correction. J. Comput. Chem., 27:1787-, 2006.
- I. A. Fedorov, Y. N. Zhuravlev, V. P. Berveno Structural and electronic properties of perylene from firstprinciples calculations // Journal of Chemical Physics 2013.V.138, N. 094509.
- Dovesi, R. CRYSTAL09 User’s Manual / R. Dovesi, V.R. Saunders, C. Roetti [et al.] // Torino: University of Torino. — 2010.
- CRYSTAL Basis Sets Library [Электронный ресурс] URL: (дата обращения 30.07.2014).
- Qiang Zhu Constrained evolutionary algorithm for structure prediction of molecular crystals: methodology and applications / Qiang Zhu, Artem R. Oganov, Colin W. Glass and Harold T. Stokes // ActaCryst. (2012). B68, 215–226. doi:10.1107/S0108768112017466.
- Odutola J.A. Molecular beam electric deflection study of ammonia polymers /J. A. Odutola, T. R. Dyke, B. J. Howard, and J. S. Muenter // The Journal of Chemical Physics (1979) 70, 4884; doi: 10.1063/1.437366.
- A. Daniel Boese From ab initio quantum chemistry to molecular dynamics:The delicate case of hydrogen bonding in ammonia / A. Daniel Boese, Amalendu Chandra, Dominik Marx // Journal of Chemical Physics. 2003. V. 119, N. 12. P.5965.
- E. R. Johnson. A post-Hartree-Fock model of intermolecular interactions: Inclusion of higher-order corrections / E. R. Johnson and A. D. Becke // The Journal of Chemical Physics. (2006) 124, 174104.[schema type=»book» name=»ИССЛЕДОВАНИЕ СТРУКТУРЫ МОЛЕКУЛЫ, ДИМЕРА, ТРИМЕРА И КРИСТАЛЛА АММИАКА» description=»Методами компьютерного моделирования, с использованием гибридного обменно-корреляционного потенциала B3LYP в базисах TZVP, 3-1p1G и 6-31d1G, исследованы структуры молекулы, димеров, тримеров и эле-ментарной ячейки кристаллического аммиака, получены заселенность химических связей, избыточные заряды на атомах, некоторые термодинамические и энергетические параметры.» author=»Клишин Юрий Александрович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-05-24″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.01.2015_01(10)» ebook=»yes» ]