В работе рассматриваются и исследуются параллельные алгоритмы (ПА) для задач аэрогидродинамики, основанные на декомпозиции расчетной области и использовании параллельных методов решения задач линейной алгебры. Во многих случаях с помощью параллельных вычислений удается минимизировать время расчета, что позволяет получить результаты в реальном масштабе времени. В настоящее время имеется большая библиография по параллельным вычислениям. Стоит привести работы следующих авторов [1],[5]–[11].
Выбрана конечно-разностная задача для модели обтекания профиля крыла дозвуковым потоком вязкого теплопроводного газа, построенная на основе схем расщепления по физическим процессам и пространственным направлениям [3] – [4]. Параллельный алгоритм с учетом различной топологии связи между вычислительными устройствами строится для всех дробных шагов неявной разностной схемы, однако более подробно описаны два первых шага схемы расщепления. Учитывая структуру разностной матрицы на первом дробном шаге, уравнения системы можно рассчитывать независимо друг от друга, по-разному организуя параллельные вычисления, что влияет на межпроцессорный обмен, и в конечном счете на время расчета алгоритма.
Рассмотрим системы с программируемой топологией межпроцессорных связей и распределенной памятью. Использование схем расщепления приводит к обращению ленточных матриц. Одним из экономичных прямых методов их решения является метод скалярной прогонки.
На первом дробном шаге для нахождения соответствующих параметров искомого вектора газодинамических переменных, независимо решается четыре системы ленточных уравнения вида:
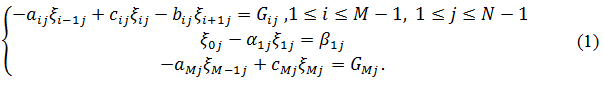
Для каждого уравнения коэффициенты и правая часть рассчитываются по своим формулам. Вычисление правой части требует обмена между процессорами.
Рассмотрим параллельную организацию вычислений при различной организации топологии сети передачи данных.
Пусть каждый процессор рассчитывает блочную строку 
которая может состоять из одного уравнения системы (1) (случай, когда число узлов по второму направлению равно числу процессоров) или из нескольких уравнений (выбирается число узлов кратное числу процессоров для равномерной загрузки вычислительных устройств). Здесь параллельный алгоритм строится за счет декомпозиции расчетной области. Так как межпроцессорных обменов нет, то время расчета пропорционально размерности области (см. табл. 1) .
При смене направления интегрирования происходит транспонирование массива данных, что приводит к росту накладных расходов.
При втором способе организации вычислений используется алгоритм параллельной прогонки [8] последовательно по обоим пространственным направлениям, позволяющий избежать транспонирования матрицы данных. Однако при этом необходим межпроцессорный обмен информацией. Число расчетных узлов сеточной области (по каждой пространственной переменной), по-прежнему, кратно числу процессоров. Организацию вычислений можно строить уже по другому параллельному алгоритму, коммутируя матричную топологию сети передачи данных (см. табл.1).
Таблица 1.
Расчет параметров параллельных алгоритмов для ленточного уравнения на сетке узлов размерности M × N
Отметим, что формирование оценок направлено на предсказание более точного времени выполнения параллельного алгоритма, поэтому при оценке трудоемкости коммуникационных операций, кроме времени обмена, указанного в таблице, необходимо учесть и время латентности, которое для имеющейся в ЮФУ гибридной вычислительной системы составляет
t=1.82 /10 6 c [10].
На первом дробном шаге можно использовать концепцию крупнозернистого параллелизма рассматривая вычисление каждого из четырех балансовых уравнений как независимую ветвь параллельного алгоритма.
При расчете второго дробного шага, в случае линейной коммутации процессоров, при смене направления интегрирования разностного уравнения, происходит блочное транспонирование матрицы значений (насчитанных на первом дробном шаге). Необходим обмен данными между всеми вычислительными устройствами рабочего поля. Для передачи информации между процессорами можно по-разному организовать параллельный обмен, программируя различные линии коммутации между процессорами вычислительной системы. При полнодоступном коммутаторе связи крупноблочное транспонирование матрицы можно произвести за р-1 шаг, используя циклический обмен между процессорами [9, 11]. Если для транспонирования матрицы размерности MxN используется алгоритм Паркинсона [2], то время обмена между р процессорами с универсальной коммутацией связи составит величину
– характерное время операции обмена одним словом). После транспонирования матрицы организация расчетов по второму направлению проводится аналогично описанному ранее.
Можно рассмотреть и третий способ организации вычислений. Начальная конечно-разностная задача расщепляется только по физическим процессам. Тогда для расчета дробных шагов можно использовать алгоритм параллельной матричной прогонки [7].
Представленные параллельные алгоритмы являются не единственными. В дальнейшем предполагается провести их сравнение с другими известными алгоритмами.
Список литературы:
- Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.:БХВ-Петербург, 2004. С.134‑154.
- Сухинов. А.И. Двумерные схемы расщепления и некоторые их приложения. ‑ М.:МАКС Пресс. 2005.408 с.
- Ковеня В.М., Слюняев А.Ю. Алгоритмы расщепления при решении уравнений Навье-Стокса // ЖВМиМФ. Т.49, № 4.
- Гамолина И.Э., Дурягина В.В., Семенистый В.В. Дозвуковое обтекание профилей // Известия ЮФУ. Технические науки. 2013.
№ 4. С. 61‑67. - Сухинов А.И., Чистяков А.Е., Алексеенко Е.В. Численная реализация трехмерной модели гидродинамики для мелководных водоемов на супервычислительной системе // Математическое моделирование. 2011. T23:3. С. 3–21.
- НиколаевИ. A., СухиновА. И., ХаринаО. Д.О распараллеливании треугольных итерационных методов на специализированной многопроцессорной системе //Автоматика и телемеханика. 1986.
№ 5. С. 135–142. - Акимова Е.Н. Распараллеливание алгоритма матричной прогонки //Математическое моделирование. 1994. Т.6. № 9. С. 61‑67.
- Яненко Н.Н., Коновалов А.Н., Бугров А.Н., Шустов Г.В. Об организации параллельных вычислений и распараллеливание прогонки // Численные методы механики сплошных сред. 1978. №7. С.136‑139.
- Ковеня.В.М.,Николаев И.А.,Луцкий Я.А.,Нестерова Г.Г., Черный С.Г. Параллельное решение задачи стационарного обтекания на МВС// Комплексы программ математической физики и архитектуры ЭВМ: Труды Школы – семинара. Красноярск. 1984. С.158–168.
- СухиновА.И.,ЛапинД.В.,ЧистяковА.Е. Моделирование прямых и обратных задач диффузии-конвекции на многопроцессорных системах для прогноза и ретроспективности анализа водных экосистем // Труды конференции «Параллельные вычислительные системы (ПАВТ)». Челябинск. 2013. С.248‑257.
- Акимова Е.Н., Белоусов Д.В.Параллельные алгоритмы решения СЛАУ с блочно-трехдиагональными матрицами на многопроцессорных вычислителях // Труды международной научной конференции «Параллельные вычислительные технологии’2011″. Челябинск: ЮУрГУ. 2011. С. 27–[schema type=»book» name=»ИССЛЕДОВАНИЕ ПАРАЛЛЕЛЬНЫХ АЛГОРИТМОВ ДЛЯ ЗАДАЧ АЭРОДИНАМИКИ НА ОСНОВЕ СХЕМ РАСЩЕПЛЕНИЯ » author=»Семенистый Владимир Васильевич, Гамолина Ирина Эдуардовна» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-05-24″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_ 30.01.2015_01(10)» ebook=»yes» ]