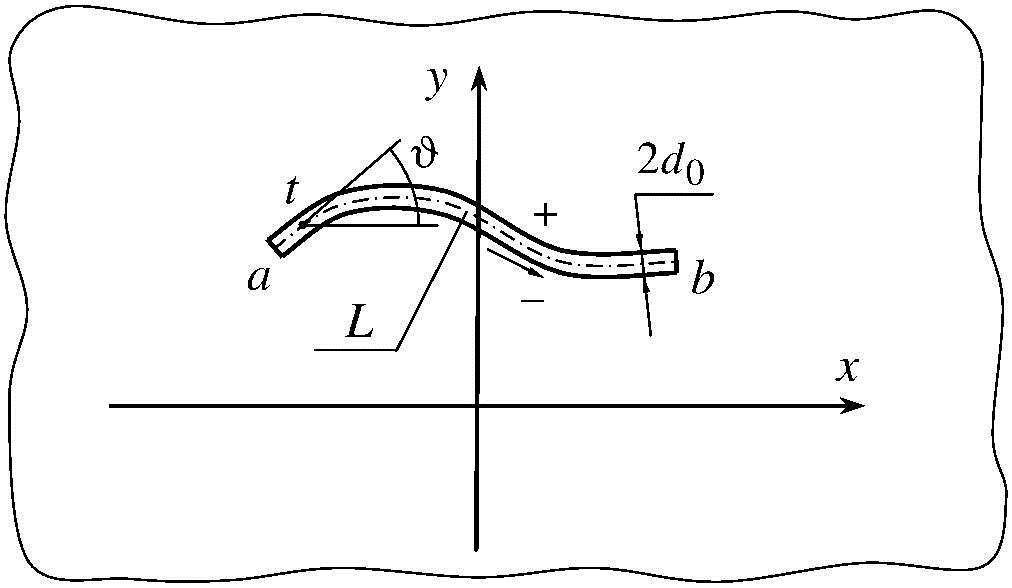
Рисунок 1. Анизотропная пластина с упругим включением
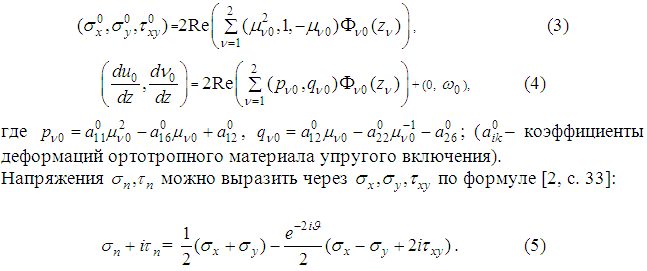
Используя формулы (3) и (5) можно выразить напряжения через потенциалы Лехницкого:
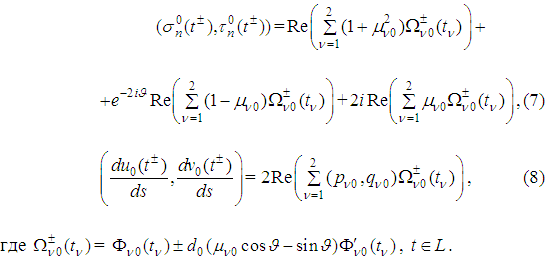
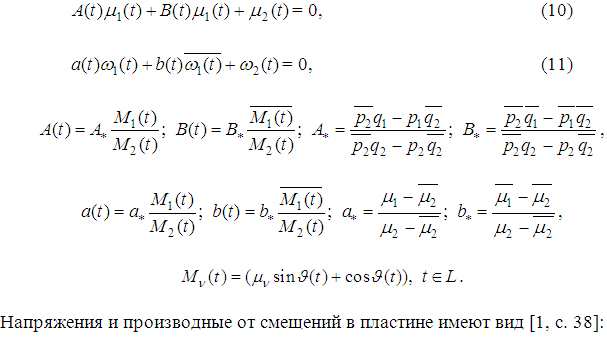
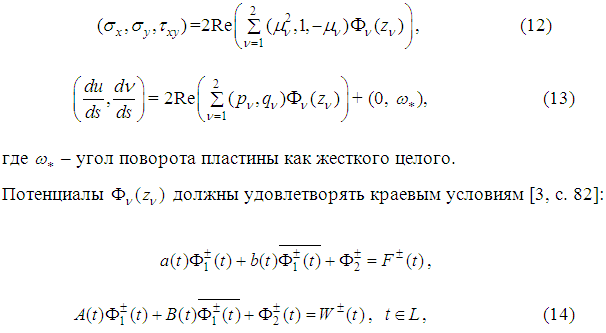
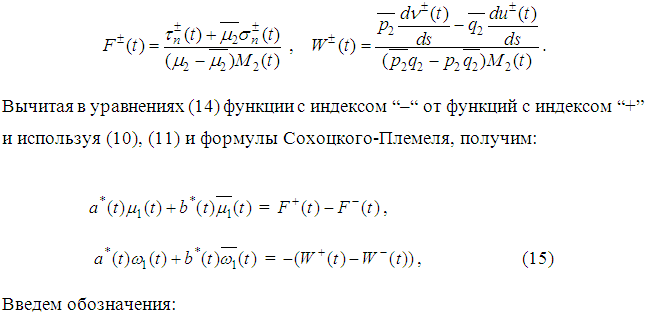
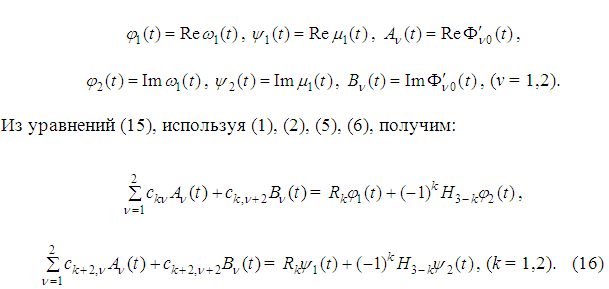
Рисунок 2. Зависимость КИН от параметров упругого включения
Значение 
= 0 соответствует случаю разреза вдоль дуги окружности. Как видно из рис. 2, жесткостные параметры криволинейного упругого включения существенно влияют на величину КИН в вершинах включения в анизотропной пластине.
Список литературы:
- Лехницкий С.Г.Анизотропные пластинки.– М.: Гостехтеоретиздат, 1957. – 464 с.
- Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. – М.: Наука, 1966. – 707 с.
- Максименко В.Н., Зорин С.А. Расчет напряженно-деформированного состояния анизотропной пластины с эллиптическим отверстием и тонкими упругими включениями //Механика твердого тела. Известия РАН. №2. – 2008. – С. 79-89.[schema type=»book» name=»ЗАДАЧА РАСЧЕТА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ АНИЗОТРОПНОЙ ПЛАСТИНЫ С ТОНКИМ УПРУГИМ ВКЛЮЧЕНИЕМ» description=»Предлагается подход к исследованию влияния тонкого упругого включения, расположенного вдоль гладкой кривой, на напряженное состояние неограни-ченной анизотропной пластины. Упругое включение рассматривается как анизотропная пластина с конечными размерами. Предполагается, что на границе контакта упругого включения и пластины осуществляется идеальное механическое сцепление. Задача сводится к системе двух сингулярных интегральных уравнений, которая решается численно. Приводятся некоторые численные результаты анализа коэффициентов интенсивности напряжений в пластине.» author=»Зорин Сергей Анатольевич» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-01-24″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_31.10.15_10(19)» ebook=»yes» ]