В данной статье исследуется асимптотическое поведение гидравлического скачка в условиях теории мелкой воды, то есть, когда отношение
h0/L=e (0<e «1)
выполняется для рассматриваемой гидравлической волны в условиях мелководья. Здесь h0 – глубина невозмущенного океана, L – длина волны, а e – малый параметр задачи.
- Постановка задачи.
В некоторый момент времени, который мы примем за начальный t=0, фронт волны достигает точки O (см. рисунок), справа от которой глубина океана начинает медленно убывать.
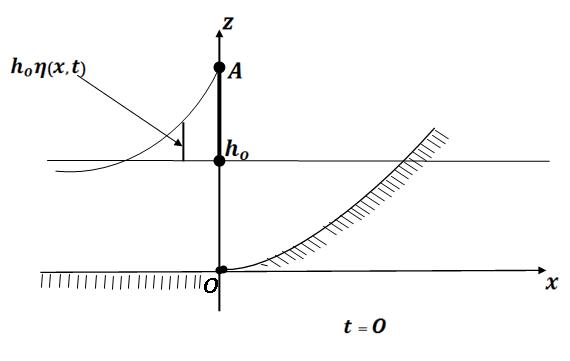
Известно, что в случае прямолинейного дна в условиях мелководья, вертикальная компонента скорости жидкости имеет более высокий порядок малости чем горизонтальная v, и течение в таких волнах с точностью до малых O(e2) является одномерным. Как было отмечено в [1], движение жидкости в случае прямолинейного дна описывается адиабатической нестационарной системой уравнений (1.1) Ù(1.2) газовой динамики с показателем адиабаты æ=2:
vt + vvx+2aax/(æ—1)=0 (1.1)
at + vax+(1/2)(æ—1)avx=0, (1.2)
где индексами обозначены частные производные, a=(gh)1/2, g — ускорение силы тяжести, h=h(x,t) — высота волны по отношению ко дну океана. Скорость звука a в теории мелкой воды может быть вычислена по формуле:
a2=dP/drh=gh, (1.3)
где P — сила давления воды в нормальном сечении волны единичной ширины l=1 и высоты h(x,t), r — плотность воды. Отметим, что P вычисляется по формуле гидростатического давления:
p=p0+rg(h—z), (1.4)
где p0 — атмосферное давление на поверхности воды, а p — гидростатическое давление жидкости. Приведем обобщение системы (1.1)Ù(1.2) на случай криволинейного дна:
z=h0j(x,e)=eh0j1(x)+O(e2), (1.5)
где j(0)=0, j(x)>0 при x>0, (j(x)=0, x<0), j¢(x)>0 при x>0, j1(x)=O(1). Функция скорости a* для случая криволинейного дна вычисляется из соотношения для силы давления воды P* в нормальном сечении волны единичной ширины и высоты h*(x,t):
P*=(1/2)rg(h*)2, (1.6)
где высота волны h*(x,t) задается формулой:
h*=h0(1+h—j), (1.7)
здесь h0h(x,t) — высота волны по отношению к невозмущенной поверхности воды (см. рисунок). Будем предполагать, что h(x,t)=O(e). Из (1.6) получаем:
(a*)2=dP*/drh*=gh*. (1.8)
Положим, что:
a*=a0(1+a*), (1.9)
где a*(x,t)=O(e). Из (1.7)-(1.9) следует:
2a*=h—j. (1.10)
Система уравнений (1.11) Ù (1.12), описывающая движение волны, получается из законов сохранения массы и изменения количества движения, записанных для элементарного объема ограниченного двумя нормальными сечениями единичной ширины, расстояние между которыми равно dx, нижнее основание объема покоится на криволинейном дне, а верхнее совпадает со свободной поверхностью воды:
vt + vvx+2a*ax/(æ—1)+h0gj¢(x)=0 (1.11)
(a*)t + v(a*)x+(1/2)(æ—1)a*vx=0. (1.12)
Последнее слагаемое в (1.11) задает реакцию дна. Ясно, что, если j(x)º0, то система (1.11)Ù(1.12) переходит в (1.1)Ù(1.2). Будем искать асимптотическое решение системы (1.11)Ù(1.12) при следующих граничных и начальном условиях:
А) На криволинейном дне нормальная составляющая скорости частиц жидкости vn должна равняться нулю. Учитывая, что vn=vcosb+wcosg, b и g углы между нормалью к поверхности дна и осями ox и oz соответственно, а w — вертикальная составляющая скорости, w=O(e2), имеем vn=0 с точностью до малых O(e2).
Б) На фронте волны искомые функции испытывают разрывы, соотношения для которых будут определены ниже.
В) Для получения начального условия предполагается, что профиль волны известен при t=0 т.е. h(x,0)=ef(x). Из (1.10) получаем начальные условия:
2a*(x,0)=ef(x), (1.13)
где f(x)>0 при x£0.
- Линейное решение.
Всюду в дальнейшем будем предполагать, что:
j¢(x)=O(e2).
В области изменения искомых функций будем искать решение системы (1.11)Ù(1.12) в виде асимптотических разложений:
M(x,t,e)=eM1(x,t)+e2M2(x,t)+… (2.1)
a*(x,t,e)=ea1*(x,t)+e2a2*(x,t)+… (2.2)
h(x,t,e)=eh1(x,t)+e2h2(x,t)+… (2.3)
Подставляя (2.1)-(2.3) в (1.11), (1.12) получаем:
(M1)t+2a0(a1*)x(æ—1)-1=0 (2.4)
2(a1*)t(æ—1)-1+a0(M1)x =0. (2.5)
Исключая из (2.4), (2.5) M1 получаем волновое уравнение для a1*:
(a1*)tt =a02(a1*)xx (2.6)
Начальные условия для (2.6) получаем из (1.13):
2a1*(x,0)=f(x). (2.7)
Решение уравнения (2.6) удовлетворяющее (2.7) имеет вид:
2a1*=f(x—a0t), при x£a0t. (2.8)
Функцию M1 можно получить, интегрируя уравнение (2.4), где a1* из (2.8). Полагая равной нулю произвольную функцию интегрирования (это в дальнейшем позволит срастить линейное и нелинейное решения), имеем:
M1=f(x—a0t), при x£a0t (2.9)
Из (2.8), (2.9) и (1.10) получаем соотношение
M1=h1—j1 , (2.10)
которое выполняется всюду в области применимости линейного решения. Как следует из (2.9) на граничной характеристике линейного решения x=a0t, имеем M1=f(0), f(0)>0 т.е. M1(x,t) испытывает скачок равный f(0), что противоречит понятию характеристики. Этот дефект линейного решения можно устранить введением нелинейного решения в области, прилегающей к фронту волны, получив предварительно условия на фронте аналогичные условиям на ударных волнах в газовой динамике. Заметим, что в линейном приближении высота волны eh0h1(x,t) над невозмущенной поверхностью воды задается формулой:
eh0h1(x,t)=eh0(f(x—a0t)+j1(x)).
- Условия на гидравлических прыжках.
Условия на гидравлических прыжках могут быть получены из законов сохранения массы и изменения количества движения, и имеют вид:
rh0(1+h—j)(N—v)=rh0(1—j)(N—v—) (3.1)
rh0(1—j)(N—v—)(v—v—)= P*— P—*, (3.2)
где N — скорость фронта волны, v— — скорость воды справа на фронте, которая получается аналогичным образом при нахождении значения M1 из (2.6), (2.4) и начального условия (2.7) записанного теперь для x³0:
2a1*(x,0)=—j1(x). (3.3)
После проведения указанных вычислений, получаем:
v—=—a0ej1(x).
В (3.2) P* вычисляется по (1.6), а P—* вычисляется из (1.6), где h=0. Асимптотическое представление системы (3.1)Ù(3.2) имеет вид:
M1=h1—j1 , (3.4)
N1=a0(1+(1/4)(æ+1)M1e—(1/4)(æ+1)j1e), (3.5)
заметим, что
eh1=(P*— P—*)/æP—*. (3.6)
Очевидно, что если в (3.4)Ù(3.5) j(x)º0, то получим соотношения, аналогичные известным соотношениям в газовой динамике [2].
- Нелинейные решения.
Построим нелинейное решение в области порядка O(e) прилегающей к фронту волны. В этой области введем переменные d, t’ по формулам:
ed=(x—a0t), t’= t, d=O(1), (4.1)
и будем искать решение системы (1.11)Ù(1.12) в виде асимптотических разложений:
M(x,t,e)=eM1(d,t’)+… (4.2)
a*(x,t,e)=ea1*(d,t’)+… (4.3)
h(x,t,e)=eh1(d,t’)+…
где M1(d,t’)=O(1), a1*(d,t’)=O(1), h1(d,t’)=O(1). Используя (4.2), (4.3) в (1.11)Ù(1.12), имеем:
M1=2a1*(æ—1)-1+y(t’) (4.4)
(M1)t’ +a0M1(M1)d + 2a0a1* (a1*)d (æ—1)-1=0, (4.5)
где y(t’) — произвольная функция интегрирования. Полагая y(t’)º0, получаем:
M1=2a1*(æ—1)-1. (4.6)
Используя (4.5), (4.6), имеем:
(M1)t’ +(1/2)a0 (æ+1)M1(M1)d =0. (4.7)
Общее решение уравнения (4.7) записанное в переменных x, t имеет вид:
M1=F(x—a0t—(1/2)a0 (æ+1)eM1t), (4.8)
где F — произвольная функция своего аргумента, которая получается из сращивания нелинейного решения (4.8) с линейным (2.9) по методу Ван-Дайка [3]. В соответствии с этим методом находим главную часть m1 нелинейного решения (4.8) при малых e :
m1=F(x—a0t). (4.9)
Затем находим главную часть линейного решения (2.9), которое совпадает с самим решением. Приравнивая главные части решений, получаем значение произвольной функции:
F(s)=f(s).
Используя это соотношение в (4.8), приходим к формуле нелинейного решения:
M1=f(x—a0t(1+ (1/2)(æ+1)eM1)). (4.10)
Заметим, что построенное нелинейное решение удовлетворяет условию на фронте волны (3.4). Действительно, это условие можно получить из сравнения (1.10) и (4.6). Очевидно, что условие (3.4) выполняется во всей области возмущенного движения жидкости. Отметим, что если j(x)º0, то рассматриваемая задача имеет точное решение типа волны Римана, удовлетворяющее условию h(x,0)=ef(x). В рассматриваемой задаче построенное асимптотическое решение (4.10) при j(x)® 0, совпадает с главной частью Римановского решения.
- Асимптотика эволюции гидравлического прыжка.
Всюду далее, будем предполагать, что начальный профиль волны является линейным и задается уравнением:
f(s)=f¢(0)s+f(0), (5.1)
где s£0, f(0)>0, f¢(0)>0. Кроме этого, считаем, что
при x®+µ функция j1(x)® q,
где заданная положительная константа q удовлетворяет условию eq<1.
Дифференциальное уравнение движения фронта волны получается из (3.5) :
d(x—a0t)/dt = a0(1/4)(æ+1)M1e — a0(1/4)(æ+1)j1e, (5.2)
где M1 вычисляется из (4.10) и (5.1):
M1 = f¢(0)(x—a0t+f(0)/f¢(0))/(1+ a0(1/2)(æ+1)f¢(0)et). (5.3)
Учитывая (5.3) и, что при больших значениях x будет j1(x)~q, уравнение фронта (5.2) принимает вид:
d(x—a0t)/dt=a0(1/4)(æ+1)e[ f¢(0)(x—a0t+f(0)/f¢(0))/(1+a0(1/2)(æ+1)f¢(0)et)—q]. (5.4)
Интегрируя (5.4), получаем траекторию фронта для больших t :
x=a0t(1—(1/2)(æ+1)qe)+C(1+a0(1/2)(æ+1)f¢(0)et)1/2—(f(0)+q)/f¢(0), (5.5)
где C — постоянная интегрирования. Используя (5.5) в (5.3), получаем, что для больших значений x функция M1(x,t) задается выражением:
M1 = f¢(0)C(1+a0(1/2)(æ+1)f¢(0)et)—1/2— q. (5.6)
Используя (3.4) и (3.6) в (5.6) получаем:
(P*— P—*)/æP—*= f¢(0)C(1+a0(1/2)(æ+1)f¢(0)et)—1/2. (5.7)
Положим, что при больших значениях x предельное значение P—* равно Pl*, где
Pl*=(1/2)rg(h0)2(1—eq)2.
Учитывая, что при больших значениях t, из (5.5) вытекает x~a0t, и поэтому соотношение (5.7) принимает вид:
P*~ Pl*+C*x—1/2, (5.8)
где константа C* получается из C умножением на некоторые положительные параметры задачи. Заметим, что (5.8) аналогично известному закону затухания плоских ударных волн Ландау:
p~p0+Cx—1/2,
где p0 и p — давление перед ударной волной и за ней соответственно.
Список литературы:
- Станюкович К.П. Неустановившиеся движения сплошной среды: монография. Наука, 1971. ¾ 854 с.
- Гриб А.А., Шарый В.А. Распространение ударной волны в водоеме с наклонным дном. Вестник ЛГУ. 1974, 3, 74-81.
- Ван-Дайк М. Методы возмущений в механике жидкости: монография. М., 1967. ¾ 310 с.[schema type=»book» name=»АСИМПТОТИКА ГИДРАВЛИЧЕСКОГО СКАЧКА НА МЕЛКОВОДЬЕ » author=»Шарый Владимир Александрович, Себельдин Анатолий Михайлович» publisher=»БАСАРАНОВИЧ ЕКАТЕРИНА» pubdate=»2017-03-24″ edition=»ЕВРАЗИЙСКИЙ СОЮЗ УЧЕНЫХ_30.04.2015_4(13)» ebook=»yes» ]

